Výpočet ΔS z termodynamických cyklů
Změnu entropie můžeme také vypočítat pomocí termodynamického cyklu. Jak jste se již dříve naučili, molární tepelná kapacita (Cp) je množství tepla potřebné ke zvýšení teploty 1 molu látky o 1 °C při konstantním tlaku. Podobně Cv je množství tepla potřebné ke zvýšení teploty 1 molu látky o 1 °C při konstantním objemu. Nárůst entropie s rostoucí teplotou na obrázku \(\PageIndex{2}\) je přibližně úměrný tepelné kapacitě látky.
Připomeňte si, že změna entropie (ΔS) souvisí s tepelným tokem (qrev) vztahem ΔS = qrev/T. Protože qrev = nCpΔT při konstantním tlaku nebo nCvΔT při konstantním objemu, kde n je počet molů přítomné látky, je změna entropie pro látku, jejíž teplota se změní z T1 na T2, následující:
\
Jak zjistíte v pokročilejších kurzech matematiky, než je zde požadováno, lze ukázat, že se rovná následujícímu:Přehled přirozených logaritmů viz Základní dovednosti 6 v kapitole 11 „Kapaliny“.
\
Podobně,
\
Takto můžeme použít kombinaci měření tepelné kapacity (rovnice 18.20 nebo rovnice 18.21) a experimentálně naměřených hodnot entalpií tání nebo vypařování, pokud se jedná o fázovou změnu (rovnice 18.21).18) k výpočtu změny entropie odpovídající změně teploty vzorku.
K výpočtu změny entropie můžeme použít termodynamický cyklus, pokud nelze přímo změřit fázovou změnu u látky, jako je síra. Jak bylo uvedeno ve cvičení v příkladu 6, elementární síra existuje ve dvou formách (část a) na obrázku \(\PageIndex{3}\): orthorombická forma s vysoce uspořádanou strukturou (Sα) a méně uspořádaná monoklinická forma (Sβ). Orthorombická forma (α) je stabilnější při pokojové teplotě, ale při teplotách vyšších než 95,3 °C (368,5 K) podléhá fázovému přechodu na monoklinickou formu (β). Přechod z Sα na Sβ lze popsat termodynamickým cyklem znázorněným v části b) na obrázku \(\PageIndex{3}\), v němž je kapalná síra meziproduktem. Změnu entropie, která doprovází přeměnu kapalné síry na Sβ (-ΔSfus(β) = ΔS3 v cyklu), nelze měřit přímo. Protože je však entropie stavovou funkcí, lze ΔS3 vypočítat z celkové změny entropie (ΔSt) pro přechod Sα-Sβ, která se rovná součtu hodnot ΔS pro jednotlivé kroky termodynamického cyklu, a to pomocí rovnice 18.20 a tabulkových termodynamických parametrů (tepelné kapacity Sα a Sβ, ΔHfus(α) a teplota tání Sα.)

Řešením ΔS3 získáme hodnotu -3,24 J/(mol-K). Jak se očekává pro přeměnu méně uspořádaného stavu (kapalina) na více uspořádaný (krystal), je ΔS3 záporná.
Jak se měří entropie
Absolutní entropie látky při libovolné teplotě nad 0 K se musí určit tak, že se vypočítají přírůstky tepla q potřebné k převedení látky z 0 K na teplotu, která nás zajímá, a pak se poměry q/T sečtou. Jsou zapotřebí dva druhy experimentálních měření:
- Entalpie spojené s jakýmikoliv fázovými změnami, kterými může látka projít v zájmovém teplotním rozsahu. Tání pevné látky a vypařování kapaliny odpovídá značnému nárůstu počtu mikrostavů, které jsou k dispozici pro přijetí tepelné energie, takže při těchto procesech bude do systému proudit energie, která tyto nové mikrostavy zaplní v míře potřebné k udržení konstantní teploty (bodu tuhnutí nebo varu); tyto přítoky tepelné energie odpovídají tepelným teplotám tání a vypařování. Například nárůst entropie spojený s tavením je právě ΔHfúze/Tm.
- Tepelná kapacita C fáze vyjadřuje množství tepla potřebné ke změně teploty o malé množství ΔT , přesněji o nekonečně malé množství dT . Zvýšení entropie vyvolané zahříváním látky v rozsahu teplot, který nezahrnuje fázový přechod, je tedy dáno součtem veličin C dT/T pro každý přírůstek teploty dT . To je samozřejmě jen integrál
\
Protože tepelná kapacita sama o sobě mírně závisí na teplotě, nejpřesnější určení absolutní entropie vyžaduje, aby se ve výše uvedeném integrálu místo konstanty C použila funkční závislost C na T.
\
Když toto není známo, lze provést řadu měření tepelné kapacity v úzkých teplotních přírůstcích ΔT a změřit plochu pod každým úsekem křivky.
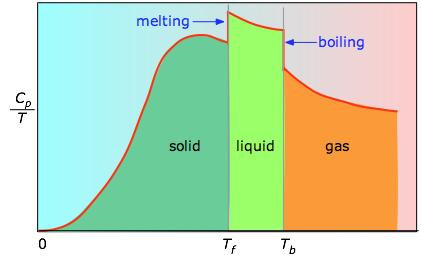
Plocha pod každým úsekem grafu představuje změnu entropie spojenou se zahříváním látky přes interval ΔT. K tomu je třeba připočítat entalpie tání, vypařování a případných fázových změn mezi pevnou a tuhou látkou. Hodnoty Cp pro teploty blízké nule se neměří přímo, ale lze je odhadnout z kvantové teorie.
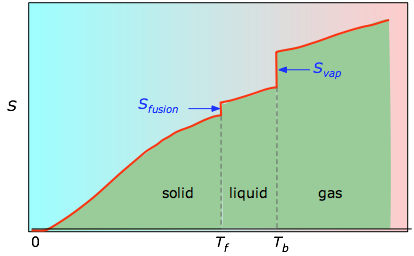
Kumulativní plochy od 0 K do libovolné teploty (převzaté z experimentálního grafu vlevo) se pak vykreslí jako funkce T a sečtou se všechny entropie fázových změn, jako je Svap = Hvap / Tb, aby se získala absolutní entropie při teplotě T.
.