Logistická rovnice (někdy nazývaná Verhulstův model nebo logistická růstová křivka) je model populačního růstu, který poprvé publikoval Pierre Verhulst (1845, 1847). Model je spojitý v čase, ale široce se používá také modifikace spojité rovnice na diskrétní kvadratickou rovnici rekurence známá jako logistická mapa.
Spojitá verze logistického modelu je popsána diferenciální rovnicí
 |
(1)
|
kde 
je malthusiánský parametr (rychlost maximálního růstu populace) a 
je tzv. nosná kapacita (tj, maximální udržitelná populace). Vydělením obou stran 
a definicí 
pak získáme diferenciální rovnici
 |
(2)
|
která je známá jako logistická rovnice a má řešení
 |
(3)
|
Funkce 
je někdy známá jako sigmoidní funkce.
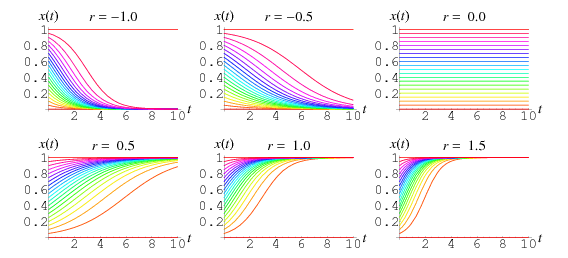
Ačkoli 
je obvykle omezena na kladnou hodnotu, jsou grafy výše uvedeného řešení zobrazeny pro různé kladné a záporné hodnoty 
a počáteční podmínky 
v rozmezí od 0,00 do 1,00 s krokem 0,05. Na obrázku je znázorněna hodnota .
Diskrétní verze logistické rovnice (3) je známá jako logistická mapa.
Křivka
 |
(4)
|
získaná z (3) se někdy nazývá logistická křivka. Podobně se normalizovaná forma rovnice (3) běžně používá jako statistické rozdělení známé jako logistické rozdělení
.