Plocha nepravidelného mnohoúhelníku

Tento článek popisuje jednoduché řešení geometrického problému, který na internetu nacházím popsaný příliš složitě. Problém spočívá ve výpočtu plochy a délky obvodu dvourozměrného uzavřeného útvaru, jako je půdorys místnosti, pozemek nebo jakýkoli jiný dvourozměrný ohraničený útvar („nepravidelný mnohoúhelník“), bez ohledu na to, jak je složitý.

Rozhodně si nedělám nárok na originalitu této metody. Její verze existují již od dob Gausse nebo i dříve. Většina článků na internetu však tuto metodu popisuje zbytečně složitě. Odkazy zahrnují článek Vzorec pro tkaničky na Wikipedii, podobně složitou metodu v článku Polygon a řadu článků, které se zdají být vypočítány spíše na demonstraci autorovy erudice než na co nejméně složité ztělesnění metody. Tento článek (PDF) ukazuje jeden z nejméně složitých (ale v žádném případě ne jednoduchých) výrazů:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\ \end{array} \pravá| + \levá|\začíná{array}{cc} x_1 & x_2 \\ y_1 & y_2\\ \končí{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\ y_2 & y_3\\ \end{array} \vpravo| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\ y_{n-2} & y_{n-1}\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\ y_{n-1} & y_0\\ \end{array} \right| \right\}$

Kde $x_n,y_n$ je vrchol mnohoúhelníku vyjádřený v kartézských souřadnicích a $\left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\ \end{array} \right|$ odkazuje na determinant s hodnotou $x_0 \times y_1 – y_0 \times x_1$

Nenechte se odradit výše uvedeným výkladem – použití této metody je jednodušší než pochopení jejích matematických základů. Při zkoumání tohoto článku jsem našel libovolné množství odpovědí na dotazy studentů, které byly tak složité, že studenta nemohly poučit. V tomto článku udělám vše pro to, aby tato metoda byla co nejjednodušší a nejpřístupnější.

Metoda je nejsnáze vyjádřitelná jako algoritmus:

• Vrcholy nepravidelného mnohoúhelníku lze reprezentovat jako kartézské souřadnice:
• Každá dvojice souřadnic se zpracuje v algoritmu součtu ploch, který vypadá takto:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Jednoduchý matematický výraz pro výše uvedené by byl:
  

  (2) Plocha nepravidelného mnohoúhelníku $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \krát y_i – y_{i+1} \times x_i}$

• POZNÁMKA: V rovnici (2) končí procházený údaj poslední poskytnutou datovou položkou, neopakuje se počáteční položka, jak je uvedeno v rovnici (1) výše. Pro mé účely, vysvětlené níže, je tato forma záměrná – v pozemkovém průzkumu by měl údaj v terénu uzavírat údaj, tj. poslední položka by se měla rovnat první. V takové aplikaci by automatické uzavření údaje podle rovnice (1) zakrývalo chyby, které je třeba vyhodnotit.

  Uživatelé mohou pro jiné účely, než je redukce údajů z pozemkového průzkumu, upřednostnit formu uvedenou ve výše uvedené rovnici (1). Pro tyto účely při zpracování jednoduše znovu vyhodnoťte první datovou položku na konci procházení nebo poskytněte datové sady, které opakují první datovou položku jako poslední.

• Zde je kompletní, funkční funkce Pythonu:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Výše uvedený argument „array“ je sada kartézských souřadnic $x,y$, tj.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). U této sady dat si všimněte, že první datový prvek se na konci opakuje.

• Tady je o něco složitější funkce Pythonu, která počítá jak plochu, tak délku obvodu:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Znovu tato připomínka: V obou výše uvedených příkladech kódu by v jiných aplikacích, než je redukce dat z pozemkových průzkumů, měla poskytnutá datová sada obsahovat kopii první datové položky jako poslední, tj.Tj. údaj by měl být explicitně uzavřen.

• Pro tyto příklady jsem zvolil Python, protože výpis v Pythonu maximalizuje algoritmický význam a zároveň minimalizuje cruft.

• Výše uvedené funkce lze snadno převést do jiných jazyků, a to téměř přímo – s výjimkou výše uvedeného sčítání obvodů, které využívá toho, že Python podporuje komplexní čísla. Pro jazyky, které nepodporují komplexní čísla, lze výsledek obvodu vytvořit takto:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formálně je délka obvodu součtem velikostí vektorů:
  

  (3) Délka obvodu $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-.y_i)^2}}$

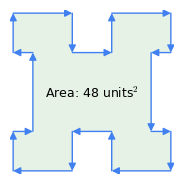
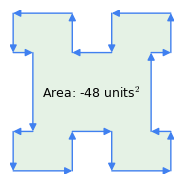Obrázek 1: Ve směru hodinových ručiček vs. vektory proti směru hodinových ručiček

Zde jsou uvedeny některé důležité vlastnosti této metody:

• Zvolený počáteční vrchol v rámci mnohoúhelníku není pro výpočet plochy ani obvodu důležitý, důležité je pouze to, aby byl obrazec uzavřený, tj.tj. poslední souřadnice by se měla rovnat první.
• „Pravidlo hodinových ručiček“: Podstatné je pořadí vektorů – pokud se obvodem prochází ve směru hodinových ručiček, je výsledek plochy kladný, pokud proti směru hodinových ručiček, je záporný (obrázek 1). Právě tato vlastnost metody odečítá plochu inflexí od složeného obrazce jako na obrázku 1 – „inflexe“ představují procházení v rámci mnohoúhelníku proti směru hodinových ručiček.
• Mnoho aplikací této metody používá původní zdroje dat tvořené polárními vektory (příkladem jsou právní popisy pozemků), ale tato metoda vyžaduje kartézské souřadnice. Převod z polárních na kartézské souřadnice je triviální, ale je důležité mít tento požadavek na paměti.
• Pro přesný výpočet plochy by měl být popisovaný polygon uzavřeným obrazcem – poslední souřadnice by se měla rovnat první. U aplikací, které používají data z terénu tvořená délkovými vektory, jež jsou následně převedeny do kartézského tvaru, je dobré porovnat počáteční a koncové kartézské souřadnice – měly by se rovnat. Například starší pozemkové mapy (před érou levného výkonu počítačů) tímto testem pravidelně neprojdou.

Tato část je plně funkční plošný/perimetrický počítač, který dokáže zpracovávat zadané dvojice kartézských nebo polárních souřadnic nebo geodetické právní popisy. Stačí zvolit typ dat (kartézské souřadnice x,y, polární souřadnice m,θ nebo geodetický právní popis) a zadat (nebo vložit) data do níže uvedené oblasti pro zadávání dat. Pro seznámení a procvičení si můžete vybrat také vzorové datové sady.

Vzhledem k bezpečnostním otázkám prohlížeče, abyste se vyhnuli nadměrnému psaní a importovali značné množství dat z jiného zdroje, budou muset čtenáři používat svou systémovou schránku. Stačí zkopírovat data do schránky ve zdrojové aplikaci, poté kliknout na oblast pro zadávání dat níže a stisknout Crtl+A pro výběr všech, Ctrl+V pro pasování dat odjinud a Ctrl+C pro zkopírování vlastních zadaných dat. Většina prohlížečů obsahuje funkce schránky také jako položky nabídky.

Volba typu dat:

kartézský (x,y)

polární (m,θ)

Popis průzkumu

Oblast zadávání dat: Zvolte vše: Kopírovat: Ctrl+A | Kopírovat: Ctrl+C | Vložit:

Oblast grafu:

Sorry – your browser does not support the graphic ability this feature requires –
consider installing Google Chrome or Firefox.

Možnosti:

Čáry

Šipky

Počátek

Střed

Jednotka délky:

Šířka čáry:

Obráceně

Výsledky:Vybrat vše: Kopírovat: Ctrl+A | Kopírovat: Ctrl+C | Vložit:

Plošný/obvodový počítač má tři vstupní režimy:

• Kartézské (x,y) souřadnicové páry:

  • Každá souřadnice je dvojrozměrná poloha s vodorovnou (x) a svislou (y) částí (kartézská souřadnice).
  • Souřadnice nejsou kumulativní – každá samostatně popisuje svou polohu.
  • Takže čtverec by byl:
    • 0,0 (počátek)
    • 0,100 (nahoru)
    • 100,100 (doprava)
    • 100,0 (dolů)
    • 0,0 (zpět k počátku)
  

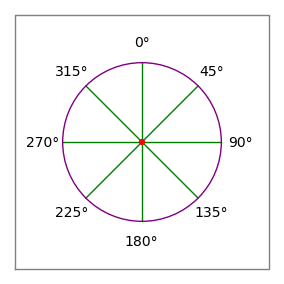  Obrázek 2: Kompasová růžice

  • Čárky ve výše uvedeném příkladu slouží pouze k seskupení dvojic dat pro čtenáře – pro analyzátor dat v počítači Area nemají žádný význam.
  • Parser je natolik robustní, že výše uvedený příklad lze vložit do datového vstupu počítače oblasti a bude fungovat (vyzkoušejte si to).
  • Jediným omezením je, že vysvětlující komentáře nemohou obsahovat čísla.

• Polární (m,θ) souřadnicové páry:

• Každá souřadnice se skládá ze vzdálenosti a úhlu ve stupních (polární vektor).
• Úhly se řídí konvencí kompasu – 0 stupňů je nahoru nebo „sever“, 90 stupňů je doprava nebo „východ“ (obrázek 2).
• Na rozdíl od předchozí kartézské formy jsou tyto souřadnice kumulativní – každý nový vektor se přičítá k současné poloze.
• Čtverec by tedy byl:
  • 100,0 (nahoru)
  • 100,90 (doprava)
  • 100,180 (dolů)
  • 100,270 (zpět k počátku)
• Jako dříve, tento příklad bude fungovat, pokud jej vložíte do oblasti pro zadávání dat v počítači a zvolíte polární režim.
• Upozorňujeme na polární souřadnice, že počátek je implicitní a přednastavený na x = 0, y = 0.

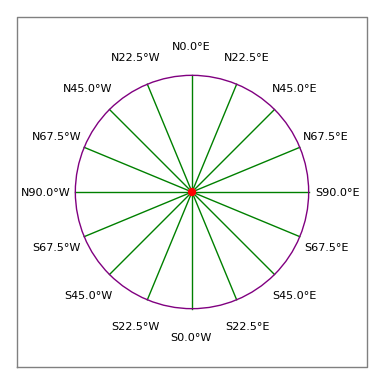Obrázek 3: Geodetická kompasová růžice

Právní popis:

• Nejprve vysvětlení vztahu mezi volbou „Jednotky délky“ a zobrazením výsledků:
  • Pro každý polygon se vypočítá seznam výsledků plochy s použitím pevné sady běžných jednotek plochy (stop2, metrů2 atd.). Aby měl tento seznam ploch smysl, musí být známy vstupní délkové jednotky.
  • V kartézském a polárním režimu nemají datové položky žádné jednotky, takže uživatel volí, jaké jednotky délkám přiřadí. Když tedy uživatel změní délkové jednotky, změní se hodnoty ploch, změní se popisky délek, ale hodnoty délek se nezmění.
  • V režimu Survey obsahuje právní popis délkové jednotky (stopy, metry atd.), což znamená, že délkové jednotky jsou předem definovány zdrojem. Když tedy uživatel změní délkové jednotky, změní se tím popisky a hodnoty délek, nikoli hodnoty ploch.
• Parser survey description je zdaleka nejméně spolehlivý ze všech tří metod parsování dat – je to spíše experiment než robustní metoda převodu dat.
• Tento parser jsem napsal tak, že jsem si stáhl několik právních popisů (které jsou uvedeny jako příklady ve výše uvedeném kalkulátoru) a ladil kód parseru, dokud se nepodařilo všechny úspěšně dekódovat.

Kritéria „úspěchu“ byla, aby výsledek měl stejnou plochu čtverce, jakou tvrdí popis, a aby se obrázek „blížil“.

• Termín „uzavřenost“, a zejména chyba uzavřenosti, se v geodetických pracích používá k popisu míry, do jaké se koncový bod geodetické trasy rovná počátečnímu bodu. Ve skutečnosti je to málokdy pravda – chyby uzávěrky obvykle vznikají v důsledku chyb při práci v terénu a starší průzkumy, publikované před nástupem levné výpočetní techniky, mají tendenci mít poměrně špatné uzávěrky a také divoce nepřesné odhady čtvercové plochy.
• Měřický právní popis je formální způsob popisu pozemku – jeho forma a syntaxe vznikala po desetiletí podle vzájemně přijímaných, poněkud svévolných konvencí, které sdílejí geodeti.
• Pro tento plošný/obvodový počítač musí zadávané údaje dodržovat určité přísné konvence, které některé, ale ne všechny právní popisy dodržují. Základními prvky jsou:
  • Existence výrazu „počáteční bod“, který odděluje určitý předběžný obsah od obsahu popisujícího rozměry popisované parcely. V některých dokumentech se uvádí „skutečný počáteční bod“, v některých „skutečný počáteční bod“ a v některých „počáteční bod“. Úspěšný parser musí odstranit obsah před touto frází a zachovat vše za ní.
  • Řada frází, které popisují zvláštní druh polárního vektoru používaného geodety:
    • Slovo „sever“ nebo „jih“ nebo jeho zkratka „N“ nebo „S“.
    • Pak úhel vyjádřený ve stupních, minutách a sekundách.
    • Pak slovo „východ“ nebo „západ“ nebo jeho zkratka „E“ nebo „W“.
    • Potom vzdálenost.
    • Potom jednotka vzdálenosti – stopy, metry atd.
• Zde jsou uvedeny různé příklady geodetických vektorů ze vzorových právních descrtiptions:
  • N 2°0’0″ W – 63,50 stop
  • N90°00’00 „W podél linie rovnoběžné se zmíněnou severní linií ve vzdálenosti 6,00 stop
  • severně 0°06’O0″ západně ve vzdálenosti 554.86 stop
  • S. 22°41′55″E. 174,10 stop
• Všimněte si u výše uvedených příkladů, že všechny mají odlišnou syntaxi. Existuje mnoho právních popisů, které tento parser úspěšně nedekóduje, a to jen proto, že jsem se nepokusil začlenit jejich syntaxi. Je však důležité dodat, že skutečně robustní parser pro množství existujících právních popisů by musel být stejně chytrý jako Watson.
• Uživatelé tohoto plošného/obvodového počítače se možná budou chtít vyhnout zadávání prostých textových právních popisů a doufat, že na to parser přijde. Pro přímé ruční zadávání (nebo pro vytvoření seznamu traverz jinde pro import) použijte tuto konvenci:
  • Pamatujte si, že přijatelný záznam traverzu se skládá ze slova „Sever“ nebo „Jih“ nebo písmene „N“ nebo „S“, za kterým následují až tři čísla udávající úhlové stupně, minuty a sekundy, za kterými následuje slovo „Východ“ nebo „Západ“ nebo písmeno „E“ nebo „W“, za kterým následuje vzdálenost a za ní jednotka vzdálenosti.
  • Přijatelný zápis by tedy byl „N 30 15 45 W 100 stop“, což znamená traverzu o délce 100 stop směřující 30 stupňů, 15 minut a 45 sekund západně od severu (tj. zhruba 330 kompasových stupňů, viz obrázek 3).
  • Zápisy minut a sekund lze vynechat, pokud jsou rovny nule nebo pokud je zápis v desetinných stupních nebo stupních a desetinných minutách.
• Převod tištěného právního popisu na tyto zápisy není obtížný a existuje řada způsobů, jak odhalit chyby. Pokud po zadání všech traverz nemá obrázek žádnou chybu v uzávěru a hlásí stejnou čtvercovou plochu jako originál, je pravděpodobné, že jsou zápisy správné (nebo mají stejné chyby jako původní popis).
• Pokud se po zadání právního popisu tímto způsobem objeví nepřijatelná chyba v uzávěru nebo je chybná čtvercová plocha, nezapomeňte, že původní údaje mohou být chybné. Existuje libovolné množství právních popisů, které nikdy nebyly kontrolovány počítačovou metodou, jako je tato, a které nikdy nebyly správné.

Při prohlížení kartézských příkladů (x,y) si všimněte poměru plochy a obvodu různých tvarů. „Podivný mnohoúhelník“ má střední poměr, kruh má nejmenší poměr a Hilbertův prostor má zdaleka největší poměr. Tento poměr se rozšiřuje i do vyšších rozměrů, kde je známo, že největší objem na plochu má koule.

K příkladu s kruhem – jedná se o „jednotkový kruh“, kružnici o poloměru jedna. Pro uvedený příklad se plocha blíží hodnotě $\pi$ a obvod se blíží hodnotě $2\pi$, což jsou správné hodnoty pro jednotkovou kružnici. Aby tyto hodnoty nebyly jen přibližné, aby se přesně rovnaly $\pi$ a $2\pi$, musel by být počet stran mnohoúhelníku nekonečný. Rozhodl jsem se, že to neudělám 🙂

Příklad Hilbertova prostoru byl vygenerován pomocí algoritmu Sage se skromnou volbou řádu (aby se negenerovalo příliš mnoho dat). V principu může mít Hilbertův prostor nekonečný poměr obvodu k ploše ve dvou rozměrech nebo plochy k objemu ve třech rozměrech. Chcete-li vidět, jak složitý může Hilbertův prostor být, klikněte sem a podívejte se na Hilbertův prostor řádu 7.

Všimněte si u Hilbertova příkladu, že vypočtená plocha se blíží 1/2 pro plochu 1×1. V ideálním případě, bez nutnosti převádět čárový údaj na plošný a se správným algoritmem, by plocha byla přesně 1/2 plochy čtverce stejných rozměrů.

Režim polárního zadávání se víceméně rovná Želví grafice, pokud se nahradí nula stupňů za „nahoru“, 90 stupňů za „doprava“ atd. a pokud se každá sekvence otáčení a přesouvání sbalí do jednoho příkazu. Použití režimu polárního zadávání je snadný způsob ruční konstrukce složitého tvaru, protože vzdálenosti a úhly se snáze sledují než kartézské souřadnice.

Výše popsanou metodu výpočtu plochy pozemku jsem poprvé použil před lety, když jsem žil na venkově v Oregonu, obklopen lidmi, kteří potřebovali znát plochu a obvod svých pozemků. Setkal jsem se s mnoha šokujícími příklady, kdy realitní makléři bezostyšně podváděli lidi, kteří neměli možnost zjistit, o co jde. Při mnoha příležitostech jsem vypočítával výměru z právního popisu, abych zjistil, že tvrzení záruční listiny o výměře je šíleně nepřesné – a vždy vyšší než skutečnost.

Při jedné příležitosti jsem byl požádán, abych rozdělil nemovitost na dvě stejné části a vytvořil právní popisy pro každou z nich. Protože jsem měl nově pořízený počítač Apple II (který měl výpočetní výkon moderního ořezávátka), bylo to velmi snadné – ale při práci jsem zjistil, že celková výměra se liší asi o tři akry, tedy asi o 25 % celkové výměry. Konfrontoval jsem to s vlastnickou společností, která bezelstně odpověděla: „Vidíte tady, kde je v listině napsáno ‚více nebo méně‘?“

Při jiné příležitosti jsem začal kupovat pozemek, ale varován výše uvedenou zkušeností jsem se po obdržení pojistné smlouvy rozhodl zadat její právní popis do svého programu, abych zjistil, zda je tvrzení o výměře přesné. Ke svému zděšení jsem však zjistil, že všechny pojistky vlastnického práva k pozemkům v této části měly stejný právní popis – prvního vyměřeného pozemku. Ukázalo se, že developerská společnost se rozhodla ušetřit peníze tím, že vyměří pouze jeden z desítek pozemků nabízených k prodeji a tento právní popis uvede do všech pojistných smluv. Byli si jisti, že jim to projde – koneckonců, kdo se vyzná v matematice?“

Po dohadování s vlastnickou společností a developerem, kdy jsem se je snažil přesvědčit, aby zaplatili za průzkumy, aby právní popisy nebyly zdvořilostní výmysly, jsem to vzdal a rozhodl se pozemek nekoupit. Bylo to jako zjišťovat, jak se dělá klobása – je možné vědět příliš mnoho.

• 04.15.2013 Verze 1.3. Přidáno podrobné vysvětlení výchozího formátu dat, tj. seznamů, které opakují první datový bod jako poslední.
• 03.24.2013 Verze 1.2. Dále optimalizován parser popisu průzkumu, přidána další pole výsledných dat.
• 03.23.2013 Verze 1.1. Vylepšen parser právního popisu pro práci s více druhy popisů, přidán selektor jednotek délky a výsledný seznam ploch v běžných jednotkách.
• 03.22.2013 Verze 1.0. První veřejná verze.

.