Faktoriály najdete všude v kombinatorice, protože tam vznikly. Faktoriál vznikl jako způsob, jak vyjádřit počet uspořádání skupiny prvků, který samozřejmě zjistíme pomocí, ve své nejzákladnější podobě, násobícího pravidla počítání.
Faktoriál je jakousi neoficiální operací násobícího pravidla počítání.
Proč se nulový faktoriál rovná 1
Tady to začíná být ošemetné, protože pokud o faktoriálech uvažujeme pouze v kontextu, ve kterém jsou obvykle definovány, tj.tj. jako „součin všech kladných celých čísel menších nebo rovných danému číslu“, pak přijít na to, že 0! je jako narazit na cihlovou zeď.
Většina lidí vám řekne, že 0! je definováno jako 1, a když se zeptáte proč, řeknou jen „protože je definováno jako jedna“.
Jo, je to dost frustrující. Je to matematický ekvivalent toho, když se zeptáte rodičů, proč se musíte řídit nějakým libovolným pravidlem, které si vymysleli, a oni vám řeknou: „Protože jsem to řekl.“
Ačkoli to může být uznávaná rodičovská technika, je to mizerný způsob, jak se naučit matematiku. Tak o co jde? Jak jsme se rozhodli, že faktoriál nula se rovná jedné?“
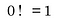
Intuitivní pochopení
Pamatujete, jak jsme si řekli, že faktoriál vznikl z matematické operace hledání počtu permutací nebo uspořádání množiny? (Poznámka: ne permutací menší množiny z větší množiny, ale právě uspořádání dané množiny.)
Nulový faktoriál si můžeme představit jako počet uspořádání nulových prvků v množině, neboli prázdné množině {}. (Pokud jste někdy studovali množiny, třeba v základech statistiky nebo diskrétní matematiky, pravděpodobně pojem prázdné množiny znáte. Je to doslova množina ničeho.“
Nyní, kdybych se vás zeptal, kolik je uspořádání jedné věci, odpověděli byste 1, protože existuje pouze jeden způsob uspořádání jedné věci. Stejná myšlenka vyplývá i zde. Naše „jedna věc“ je prázdná množina a počet uspořádání prázdné množiny je jedna. To je vše. Proto se 0! rovná 1.
Jak zjednodušovat faktorové výrazy
Teď, když máme základy za sebou, je čas na jádro našeho výukového kurzu o faktorech: zjednodušování.
Nejlepší způsob, jak vidět matematiku, je v akci. Proto jsem tu já, abych vás provedl šesti úlohami zobrazenými na obrázku v horní části tohoto příspěvku! Začneme pěkně od začátku, pak přejdeme ke kombinačnímu vzorci s čísly a pak s proměnnými a skončíme u složitějších faktoriálových výrazů.
❤ STAY CONNECTED ❤
Nenechte si ujít ani jeden matematický problém!
.