Areal af en uregelmæssig polygon

Denne artikel beskriver en simpel løsning på et geometrisk problem, som jeg finder beskrevet på alt for komplekse måder på nettet. Problemet går ud på at beregne arealet og omkredslængden af en to-dimensionel, lukket figur som f.eks. en rumplan eller et stykke jord eller en hvilken som helst anden to-dimensionel afgrænset figur (en “uregelmæssig polygon”), uanset hvor kompleks den er.

Jeg hævder bestemt ikke originalitet for denne metode. Der har eksisteret versioner siden Gauss’ tid eller før. Men de fleste online artikler beskriver metoden på unødigt komplekse måder. Referencerne omfatter artiklen om snørebåndsformlen på Wikipedia, en tilsvarende kompleks metode i artiklen om polygon og en række artikler, der tilsyneladende mere er beregnet til at demonstrere forfatterens lærdom end til at give den mindst komplekse udførelsesform af metoden. Denne artikel (PDF) viser et af de mindst komplekse (men på ingen måde simple) udtryk:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\\end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\ y_1 & y_2\\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\ y_2 & y_3\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\ y_{n-2} & y_{n-1}\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\ y_{n-1} & y_0\\\end{array} \right| \right\}$

Hvor $x_n,y_n$ er et polygonhjørne udtrykt i kartesiske koordinater, og $\left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\\\ \end{array} \right|$ refererer til en determinant, med værdien $x_0 \times y_1 – y_0 \times x_1$

Lad dig ikke afskrække af ovenstående redegørelse – det er lettere at bruge denne metode end at forstå dens matematiske grundlag. Under min research til denne artikel fandt jeg et vilkårligt antal svar på studerendes forespørgsler, der var så komplekse, at de umuligt kunne have oplyst den studerende. I denne artikel vil jeg gøre alt hvad jeg kan for at gøre denne metode så enkel og tilgængelig som muligt.

Metoden er lettest at udtrykke som en algoritme:

• En uregelmæssig polygons hjørner kan repræsenteres som kartesiske koordinater: $x,y$.
• Hvert par koordinater behandles i en algoritme til opsummering af arealet, der ser således ud:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Et simpelt matematisk udtryk for ovenstående ville være:
  

  (2) Uregelmæssigt polygonareal $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \ gange y_i – y_{i+1} \times x_i}$$

• BEMÆRK: I ligning (2) slutter den gennemløbne figur med det sidste dataelement, den gentager ikke det indledende element som vist i ligning (1) ovenfor. Af hensyn til mine formål, som forklares nedenfor, er denne form tilsigtet – i en landmåling skal feltdataene afslutte figuren, dvs. det sidste element skal være lig med det første. I en sådan anvendelse ville en automatisk lukning af figuren som i ligning (1) skjule fejl, som skal evalueres.

  Brugere kan foretrække den form, der er vist i ligning (1) ovenfor, til andre formål end reduktion af landmålingsdata. Til disse formål skal man under behandlingen blot reëvaluere det første datapunkt i slutningen af traversen eller levere datasæt, der gentager det første datapunkt som det sidste.

• Her er en komplet, fungerende Python-funktion:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Det ovenstående argument “array” er et sæt kartesiske $x,y$-koordinater, dvs.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Bemærk ved dette datasæt, at det første datapunkt gentages til sidst.

• Her er en lidt mere kompleks Python-funktion, der beregner både areal og omkredslængde:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Og igen, denne reminder: for begge ovenstående kodeeksempler gælder det, at i andre anvendelser end reduktion af landmålingens data bør det leverede datasæt indeholde en kopi af det første dataelement som det sidste, dvs.dvs. figuren bør være eksplicit lukket.

• Jeg valgte Python til disse eksempler, fordi et Python-listing maksimerer den algoritmiske betydning og samtidig minimerer cruft.

• De ovennævnte funktioner kan nemt konverteres til andre sprog, næsten direkte – bortset fra den ovenfor viste perimeter-summation, som udnytter det faktum, at Python understøtter komplekse tal. For sprog, der ikke understøtter komplekse tal, kan man skabe perimeter-resultatet på denne måde:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formelt set er perimeterlængden summen af vektorernes størrelser:
  

  (3) Perimeterlængde $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}}$

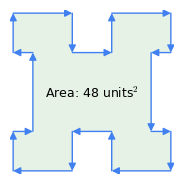
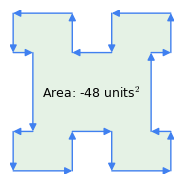Figur 1: Med uret vs. vektorer mod uret

Her er nogle vigtige egenskaber ved denne metode:

• Det valgte oprindelsespunkt inden for polygonen er irrelevant for enten areal- eller omkredsberegning, kun at figuren er lukket, dvs.dvs. at den sidste koordinat skal være lig med den første.
• “Regel med uret”: Vektorernes rækkefølge har betydning – hvis omkredsen gennemløbes med uret, er arealresultatet positivt, hvis den gennemløbes mod uret, er det negativt (figur 1). Det er denne egenskab ved metoden, der trækker arealet af bøjninger fra en kompleks figur som i figur 1 – “bøjningerne” repræsenterer en traversering mod uret inden for polygonen.
• Mange anvendelser af denne metode anvender oprindelige datakilder bestående af polære vektorer (et eksempel er landmålingens juridiske beskrivelser), men denne metode kræver kartesiske koordinater. Konverteringen fra polære til kartesiske koordinater er triviel, men det er vigtigt at huske på dette krav.
• For at opnå en nøjagtig arealberegning skal den beskrevne polygon igen være en lukket figur – den sidste koordinat skal være lig med den første. For applikationer, der anvender feltdata, der består af længdevektorer, som efterfølgende konverteres til kartesisk form, er det en god idé at sammenligne de kartesiske start- og slutkoordinater – de skal være ens. Ældre landmålinger (før æraen med billig computerkraft) fejler f.eks. jævnligt denne test.

Dette afsnit er en fuldt funktionsdygtig area/perimeter computer, der kan behandle indtastede kartesiske eller polære koordinatdatapairer, eller lovlige landmålerbeskrivelser. Vælg blot en datatype (kartesiske x,y-koordinater, polære m,θ-koordinater eller en juridisk beskrivelse) og indtast (eller indsæt) data i dataindtastningsområdet nedenfor. Du kan også vælge eksempler på datasæt for at blive fortrolig med dem og øve dig.

På grund af browsersikkerhedsproblemer, for at undgå overdreven indtastning og for at importere betydelige mængder data fra en anden kilde, skal læserne bruge deres systemklippebord. Du skal blot kopiere data til udklipsholderen i kildeprogrammet, derefter klikke på dataindtastningsområdet nedenfor og trykke på Ctrl+A for at vælge alle, Ctrl+V for at passee data fra et andet sted og Ctrl+C for at kopiere dine egne indtastede data. De fleste browsere indeholder også udklipsholderfunktioner som menupunkter.

Vælg datatype:

kartesisk (x,y)

polær (m,θ)

Survey description

Dataindtastningsområde: Vælg alle: Ctrl+A | Kopier: Ctrl+C | Indsæt: Ctrl+V

Diagramområde:

Sorry – din browser understøtter ikke den grafiske evne, som denne funktion kræver –
overvej at installere Google Chrome eller Firefox.

Optioner:

Linjer

Pile

Oprindelse

Center

Længdeenhed:

Linjebredde:

Omvendt

Resultater:Vælg alle: Ctrl+A | Kopier: Ctrl+C | Indsæt: Ctrl+V

Areal-/perimetercomputeren har tre inputtilstande:

• Cartesiske (x,y) koordinatpar:

  • Hvert koordinat er en todimensionel position med en vandret (x) og lodret (y) del (en kartesisk koordinat).
  • Koordinaterne er ikke kumulative – hver enkelt beskriver uafhængigt sin placering.
  • Så et kvadrat ville være:
  • Så et kvadrat ville være:
  • • 0,0 (oprindelse)
    • 0,100 (op)
    • 100,100 (højre)
    • 100,0 (ned)
    • 0,0 (tilbage til oprindelsen)
  

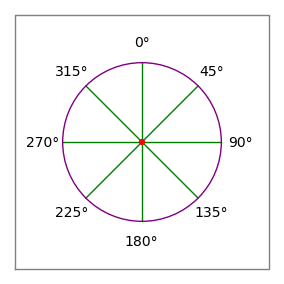  Figur 2: Kompasrose

  • Kommaerne i ovenstående eksempel er kun beregnet til at gruppere dataparrene for læseren – de har ingen betydning for områdecomputerens dataparser.
  • Parseren er robust nok til, at ovenstående eksempel kan indsættes i computerens dataindtastningsområde, og det vil fungere (prøv det).
  • Den eneste begrænsning er, at forklarende kommentarer ikke kan indeholde tal.

• Polære (m,θ)-koordinatpar:

  • Hvert koordinat består af en afstand og en vinkel i grader (en polarvektor).
  • Vinklerne følger kompaskonventionerne – 0 grader er opad eller “nord”, 90 grader er til højre eller “øst” (figur 2).
  • I modsætning til den tidligere kartesiske form er disse koordinater kumulative – hver ny vektor føjer sig til den nuværende position.
  • Så et kvadrat ville være:
  • Så et kvadrat ville være:
  • • 100,0 (op)
    • 100,90 (højre)
    • 100,180 (ned)
    • 100,270 (tilbage til oprindelsen)
  • Som tidligere vil dette eksempel fungere, hvis det indsættes i computerens dataindtastningsområde og den polære tilstand er valgt.
  • Bemærk ved polære koordinater, at oprindelsen er implicit og forudindstillet til x = 0, y = 0.
  

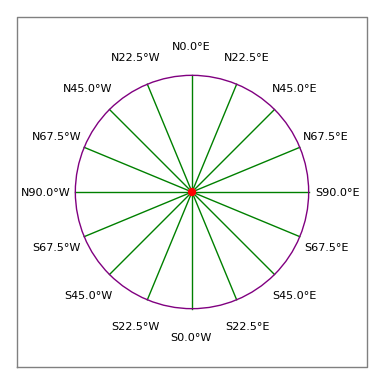  Figur 3: Landmålerens kompasrose

• Lovlig beskrivelse:

  • Først en forklaring på forholdet mellem valget af “længdeenheder” og resultatvisningen:
    • For hver polygon beregnes en liste over arealresultater ved hjælp af et fast sæt af fælles arealenheder (fod2, meter2 osv.). For at denne arealliste kan være meningsfuld, skal de indtastede længdeenheder være kendt.
    • I kartesisk og polær tilstand har dataindtastninger ingen enheder, så brugeren vælger selv, hvilke enheder der skal tildeles længderne. Så når brugeren ændrer længdeenheder, ændres arealværdierne, længdeetiketterne ændres, men det gør længdeværdierne ikke.
    • I Survey-tilstand indeholder den juridiske beskrivelse længdeenheder (fod, meter osv.), hvilket betyder, at længdeenhederne er foruddefineret af kilden. Så når brugeren ændrer længdeenheder, ændres længdeetiketterne og -værdierne, ikke arealværdierne.
  • Survey description parser er langt den mindst pålidelige af de tre data parsing-metoder – den er mere et eksperiment end en robust datakonverteringsmetode.
  • Jeg skrev denne parser ved at downloade en række juridiske beskrivelser (som er angivet som eksempler i ovenstående beregner) og indstille parserens kode, indtil alle kunne afkodes med succes.

  Kriterier for “succes” var, at resultatet skulle have det samme kvadratareal som beskrivelsen hævder, og at figuren “lukkede”.

  • Udtrykket “lukning”, og især fejl ved lukning, bruges i landmåling til at beskrive den grad, i hvilken endepunktet af landmålingens tracé er lig med begyndelsespunktet. Dette er sjældent sandt i virkeligheden – fejl i lukning skyldes normalt fejl i feltarbejdet, og ældre opmålinger, der blev offentliggjort før fremkomsten af billig computerkraft, har tendens til at have ret dårlige lukninger samt vildt upræcise skøn over kvadratarealet.
  • En survey legal description er en formel måde at beskrive et jordstykke på – dens form og syntaks er opstået gennem årtier ved hjælp af gensidigt accepterede, noget arbitrære, konventioner, som landmålerne deler.
  • For denne areal/perimeter-computer skal de indtastede data følge visse strenge konventioner, som nogle, men ikke alle, legal descriptions overholder. De vigtigste elementer er:
    • Eksistensen af udtrykket “begyndelsespunkt”, som adskiller noget indledende indhold fra det, der beskriver dimensionerne af den beskrevne parcel. I nogle dokumenter står der “sandt begyndelsespunkt”, i andre står der “reelt begyndelsespunkt” og i andre står der “begyndelsespunkt”. En vellykket parser skal fjerne indholdet før denne sætning og beholde alt efter den.
    • En række sætninger, der beskriver en særlig form for polarvektor, som anvendes af landmålingsteknikere:
      • Ordet “nord” eller “syd” eller dets forkortelse “N” eller “S”.
      • Dernæst en vinkel udtrykt i grader, minutter og sekunder.
      • Dernæst ordet “øst” eller “vest” eller dets forkortelse “E” eller “W”.
      • Dernæst en afstand.
      • Dernæst en afstandsenhed – fod, meter osv.
• Her er nogle forskellige eksempler på landmålervektorer fra eksemplet på juridiske descrtiptioner:
  • N 2°0’0″ W – 63,50 fod
  • N90°00’00 “W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
  • North 0°06’O0″ West a distance of 554.86 fod
  • S. 22 grader 41′ 55″ Ø. 174,10 fod
• Bemærk ved de ovenstående eksempler, at de alle har forskellig syntaks. Der findes mange juridiske beskrivelser, som denne parser ikke vil kunne afkode med succes, udelukkende fordi jeg ikke har forsøgt at indarbejde deres syntaks. Men det er vigtigt at tilføje, at en virkelig robust parser til de mange eksisterende juridiske beskrivelser skal være lige så smart som Watson.
• Brugere af denne område-/perimetercomputer bør måske undgå at indsende juridiske beskrivelser i ren tekst og håbe på, at parseren finder ud af det. For at foretage direkte indtastninger i hånden (eller for at oprette en liste over traverser andre steder med henblik på import) skal du bruge denne konvention:
  • Husk, at en acceptabel traverseindtastning består af ordet “North” eller “South” eller bogstavet “N” eller “S”, efterfulgt af op til tre tal, der angiver grader, minutter og sekunder for vinklen, efterfulgt af ordet “East” eller “West” eller bogstavet “E” eller “W”, efterfulgt af en distance, efterfulgt af en afstand, efterfulgt af en afstandsenhed.
  • Så en acceptabel indtastning ville være “N 30 15 15 45 W 100 fod”, hvilket betyder en travers på 100 fod, der peger 30 grader, 15 minutter og 45 sekunder vest for nord (dvs. ca. 330 kompasgrader, jf. figur 3).
  • Indtastningerne af minutter og sekunder kan springes over, hvis de er lig med nul, eller hvis indtastningen er angivet i decimalgrader eller grader og decimalminutter.
• Det er ikke svært at konvertere en trykt juridisk beskrivelse til sådanne indtastninger, og der er en række måder at opdage fejl på. Når alle traverser er blevet indtastet, og hvis figuren ikke har nogen lukkefejl og rapporterer det samme kvadratareal som originalen, er der gode chancer for, at indtastningerne er korrekte (eller de har de samme fejl som den originale beskrivelse).
• Når man har indtastet en juridisk beskrivelse på denne måde, og hvis der er en uacceptabel lukkefejl, eller kvadratarealet er forkert, skal man huske, at de originale data måske er forkerte. Der findes et vilkårligt antal juridiske beskrivelser, som aldrig er blevet kontrolleret ved hjælp af en computermetode som denne, og som aldrig har været korrekte.

Ved gennemsyn af de kartesiske (x,y) eksempler skal du lægge mærke til de forskellige figurers forhold mellem areal og omkreds. Den “mærkeligt formede polygon” har et mellemliggende forhold, cirklen har det mindste forhold, og Hilbert-rummet har langt det største forhold. Dette forhold strækker sig ind i højere dimensioner, hvor en kugle er kendt for at have det største volumen pr. overfladeareal.

Om cirkeleksemplet – det er en “enhedscirkel”, en cirkel med radius 1. For det givne eksempel er arealet tilnærmelsesvis $\pi$ og omkredsen tilnærmelsesvis $2\pi$, de rigtige værdier for en enhedscirkel. For at disse værdier skulle være mere end tilnærmelser, for at være nøjagtigt lig med $\pi$ og $2\pi$, skulle antallet af polygonsider være uendeligt. Jeg besluttede mig imod dette 🙂 🙂

Eksemplet med Hilbert-rummet blev genereret ved hjælp af en Sage-algoritme med et beskedent valg af orden (for at undgå at generere for mange data). I princippet kan et Hilbert-rum have et uendeligt forhold mellem omkreds og areal i to dimensioner eller mellem overfladeareal og volumen i tre dimensioner. For at se, hvor komplekst et Hilbert-rum kan blive, kan du klikke her for at se et Hilbert-rum af orden 7.

Bemærk ved Hilbert-eksemplet, at det beregnede areal er tæt på 1/2 for en 1×1 overflade. Ideelt set ville overfladearealet, uden at det var nødvendigt at konvertere en linjetegning til en arealtegning og med den rigtige algoritme, være præcis 1/2 af arealet for et kvadrat med samme dimensioner.

Den polære indtastningstilstand er mere eller mindre lig med Turtle graphics, hvis man erstatter nul grader med “op”, 90 grader med “højre” osv. og hvis hver dreje- og flytte-sekvens er sammenklappet til én kommando. Brug af den polære indtastningstilstand er en nem måde at konstruere en kompleks form i hånden, fordi afstande og vinkler er lettere at holde styr på end kartesiske koordinater.

Jeg brugte første gang den ovenfor beskrevne metode til beregning af landmålingens areal for mange år siden, da jeg boede på landet i Oregon, omgivet af folk, der havde brug for at kende arealet og omkredsen af deres ejendomme. Jeg stødte på mange chokerende eksempler på, at ejendomsmæglere skamløst snød folk, som ikke havde nogen mulighed for at finde ud af, hvad der foregik. Ved et vilkårligt antal lejligheder beregnede jeg et areal ud fra en juridisk beskrivelse, blot for at opdage, at garantibevisets påstand om areal var vildt unøjagtig – og altid højere end virkeligheden.

På et tidspunkt blev jeg bedt om at opdele en ejendom i to lige store dele og oprette juridiske beskrivelser for hver af dem. Da jeg havde en nyerhvervet Apple II (som havde samme processorkraft som en moderne blyantspidser), var dette meget let – men da jeg arbejdede, opdagede jeg, at det samlede areal var forkert med omkring tre acres, ca. 25 % af det samlede areal. Jeg konfronterede titelfirmaet, som skamløst svarede: “Se her, hvor der står ‘mere eller mindre’ i skødet.”

Ved en anden lejlighed påbegyndte jeg et jordkøb, men advaret af ovenstående erfaring besluttede jeg, da jeg modtog titelpolicen, at indtaste den juridiske beskrivelse i mit program for at se, om arealangivelsen var korrekt. Men til min rædsel opdagede jeg, at alle titelpolicer for parcellerne i den pågældende sektion havde den samme juridiske beskrivelse – af den første opmålte ejendom. Det viste sig, at byggeselskabet havde besluttet at spare penge ved kun at opmåle en af de snesevis af parceller, der blev udbudt til salg, og at medtage denne juridiske beskrivelse i alle ejerskiftepolicer. De var sikre på, at de ville slippe af sted med det – hvem ved trods alt noget om matematik?

Efter at have skændtes med ejendomsselskabet og bygherren og forsøgt at overtale dem til at betale for undersøgelser, så de juridiske beskrivelser ikke var høflige fiktioner, gav jeg op og besluttede mig for ikke at købe jorden. Det var som at finde ud af, hvordan pølser bliver lavet – man kan vide for meget.

• 15.04.2013 Version 1.3. Der er tilføjet en detaljeret forklaring af standarddataformatet, dvs. lister, der gentager det første datapunkt som det sidste.
• 03.24.2013 Version 1.2. Yderligere optimeret undersøgelsesbeskrivelsesparser, tilføjet flere resultatdatafelter.
• 03.23.2013 Version 1.1. Forbedret parser til juridisk beskrivelse, så den kan håndtere flere typer beskrivelser, tilføjet længdeenhedsvælger og en resultatliste over områder i fælles enheder.
• 03.22.2013 Version 1.0. Oprindelig offentlig udgivelse.