Between Borders

Har du nogensinde downloadet et dokument eller modtaget en fil fra en ven for at få den udskrevet dårligt? Der er mange mulige årsager til sådanne problemer: forskellige skrifttyper til rådighed for skaberen og printeren; forskellige styresystemer og forskellige versioner af de samme styresystemer, der afslører begrænsninger i formodede standarder på tværs af platforme; forskellige printermotorer, især når der krydses mellem blækstråler og laser; osv.

En ofte overset årsag til problemer er imidlertid forskellige papirstørrelser. Når folk i USA og Canada rækker ud efter et stykke papir til at skrive eller udskrive på, er der stor sandsynlighed for, at de rækker ud efter et stykke papir i Letter-størrelse (også kendt som US Letter), der måler 8,5 x 11 mm. Med få undtagelser rækker folk overalt andre steder ud efter et ark papir til at skrive eller udskrive på, når de rækker ud efter et stykke papir i A4-størrelse, der måler 210 mm x 297 mm.

En hurtig omregning mellem tommer og millimeter viser, at de to størrelser ikke er så forskellige:

	Millimeter		Tommer
	Bredde	Længde	Bredde	Længde
A4	210.0	297.0	8.26	11.69
Letter	215.9	279.4	8.50	11.69
Letter	215.9	279.4	8.50	11.00

Og en skildring i skala af hver sidestørrelse forstærker, at de to papirstørrelser ligger tæt på hinanden.

Det rejser spørgsmålet, hvorfor overhovedet forskellen? Hvis begge størrelser er vilkårlige, hvorfor så gide at opretholde en forskel. Svarene er lange og indviklede og ligger for det meste uden for rammerne af denne artikel. I bund og grund handler det dog om én ting: A4 er ikke en vilkårlig størrelse.

A4 beskrevet

A4 er en del af ISO 216-serien af beslægtede papirstørrelser, der er mere almindeligt kendt som A-serien. Denne serie starter med det store A0-ark, og et hurtigt kig på dette store ark papir viser, hvorfor disse forskellige ark har de størrelser, de har.

A0-ark papir er 841 mm x 1189 mm. Igen, tilsyneladende arbitrært. Multiplicer dog de to tal med hinanden, og det bliver lidt tydeligere: 841 * 1189 = 999,949 mm i kvadrat eller 0,999949 m i kvadrat (dvs. lige en lille smule under en kvadratmeter papir). I praksis indeholder et A0-ark en kvadratmeter papir.

Så hvorfor ikke gøre det til et ark på 1 m x 1 m? På grund af en anden ikke-arbitrisk betragtning: formatforholdet eller forholdet mellem højden og bredden af hvert ark.

1189/841 = 1,413793103448276. Ikke særlig mindeværdigt, medmindre man er matematisk kikset nok til at se ligheden mellem det og √2 (kvadratroden af 2, et irrationelt tal, der starter således: 1.414213562373095). Hvis man afrunder begge tal til fire betydende cifre, får man den samme værdi: 1,414.

Så er størrelsesforholdet for et A0-ark papir, igen af praktiske årsager, 1 i forhold til kvadratroden af to eller 1:√2. Og igen hører jeg råbene: “Og hvad så!”

Et forhold på 1:√2 er mere end en matematisk mærkværdighed. Det har ikke et smart navn, som det berømte gyldne snit eller den gyldne middelvej. Det har dog en smart egenskab. Hvis du deler et rektangel med siderne 1:√2 langs den længste side, har det mindre rektangel, du skaber, det samme størrelsesforhold. (Markus Kuhn foreslog i korrespondancen, at vi kalder forholdet for Lichtenberg-forholdet, efter professor Georg Christoph Lichtenberg, den tyske oplysningsmand, som først foreslog forholdet som grundlag for papirformater i 1786.)

Vi vender tilbage til forholdet (navngivet eller ej) og dets smarte egenskab: Hvis vi starter med et stort stykke A0-papir:

Vi kan nemt og hurtigt udlede alle de andre størrelser i A-serien ved at folde eller dele dem således:

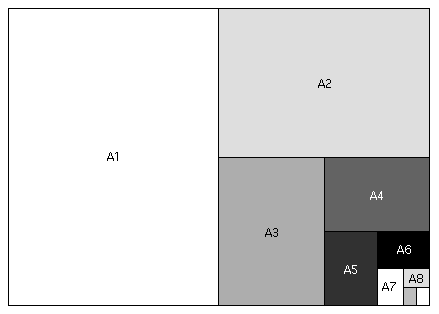
Mindre visuelt er ethvert ark papir i A-serien lige så langt som det næststørste ark er bredt og halvt så bredt som det næststørste ark er langt. Det vil sige:

Bladnavn	Bredde (mm)	Længde (mm)
A0	841	1189
A1	A1	594		841
A2	420	594
A3	297	420
A4	210	210		297
A5	148	210		210
A6	105	148
A7	74	74		105
A8	52	75

Der er andre fordele ved dette forhold mellem papirstørrelser, ikke mindst, når du ønsker at skalere et bestemt layout. Hvis du nogensinde har undret dig over, hvorfor fotokopieringsmaskiner tilbyder en 71 % reduktionsmulighed, behøver du ikke spekulere mere: 0,71 er omtrent lig med (√2)/2 eller √0,5. Dette gør den perfekt til at reducere et A3-layout til et A4-ark, eller et A4-layout til et A5-ark eller, mere almindeligt, til at reducere to A4-ark side om side – f.eks. i en journal – pænt og uden besvær til et A4-ark. Den lige så almindelige 141%-indstilling er naturligvis perfekt til at forstørre fra et ark i A-serien op til det næste (f.eks. fra A4 til A3). Det vigtigste er, at fordi hvert ark har det samme formatforhold, bevarer objekter deres relative form: firkanter bliver ikke til rektangler og cirkler bliver ikke til ellipser.

Om ikke andet gør dette konstante forhold det nemmere at arbejde med papir i A-serien end ældre papirstørrelser som Brief (13˝ x 16˝, og kilden til de “briefs”, som advokater stadig bruger) eller Foolscap (27˝ x 17˝) og dets afledte papir i næsten bogstavstørrelse, Foolscap Quarto (13˝ x 17˝) og Foolscap Quarto (13.5˝ x 8,5˝, der almindeligvis, om end fejlagtigt, kaldes “Foolscap”).

Lægges der en klar forbindelse til det metriske (eller mere korrekt SI-) målesystem til, er den stigende popularitet af papir i A-serien ret let at forstå: efterhånden som verden langsomt men sikkert er blevet metrisk, er papir i A-serien blevet mere populært. I Australien blev det metriske system f.eks. officielt indført i 1974, samme år som A-papir (og beslægtede serier som C-serien til konvolutter) begyndte at blive standard.

US Letter Described

Den klare forbindelse til det metriske system er også en delvis forklaring på den fortsatte brug af papir i Letter-størrelse i USA og Canada. USA er næsten det eneste land, der er tilbage, som ikke har skiftet fra ikke-metriske mål, hvilket gør de særlige fordele ved A4 mindre indlysende. Desuden er de amerikanske papirstørrelser, selv om de er så vilkårlige, som det nogle gange hævdes, ikke umulige at arbejde med.

Der findes ikke noget afledt udgangspunkt (svarende til 1 kvadratmeter for A0) for amerikanske papirstørrelser, men de to mest populære størrelser – Letter og Tabloid – er en del af en gammel standard fra American National Standard Institute for teknisk tegnepapir. Denne standard (ANSI/ASME Y14.1) havde fem papirstørrelser, der svingede frem og tilbage mellem to forskellige størrelsesforhold:

Bladnavn	Bredde (˝)	Længde (˝)	Læseforhold
A (Letter)	8.5		11.0		1.294
B (Tabloid)		11.0	17.0		1.545
C	17.0	22.0	1.294
D	22,0	34,0		1,545
E	34.0	44.0	1.294

Dette er ikke så elegant eller praktisk som papir i A-serien, men det er ikke særlig vanskeligt at forstørre og formindske bestemte layouts, samtidig med at man bevarer de interne relationer. Man skal blot springe en papirstørrelse over, når man bevæger sig i begge retninger.

Det er værd at bemærke, at ingen af de to størrelsesforhold har nogen særlige matematiske egenskaber. Og at der er to størrelsesforhold er ikke overraskende: fold ethvert rektangel på midten, som ikke har sider i forholdet 1:√2, og det mindre rektangels sider vil stå i et andet forhold til hinanden. Fold det mindre rektangel på midten igen, og dette tredje rektangel vil have siderne i samme forhold som det, du startede med.

Denne simple egenskab er grunden til, at rektangler med sider i forholdet 1:√2 er så smarte: de er de eneste, hvor de to forhold, du får ved at folde frem og tilbage, er ækvivalente og indbyrdes ombyttelige.

Og den blotte nytte af denne ombyttelighed er grunden til, at jeg tror, at ældre papirstørrelser som US Letter med tiden vil forsvinde, selv i USA. For eksempel anerkender den nuværende version af den ovennævnte ANSI-standard – ANSI/ASME Y14.1m-1995 – kun de ældre papirstørrelser til ældre formål, idet A-seriepapiret er den foretrukne amerikanske standard for tekniske tegninger.

Og jeg har desuden forstået, at A-papir – især A4-papir – langsomt er ved at blive normen på amerikanske colleges og universiteter, om ikke andet så for at gøre det lettere for studerende og ansatte at fotokopiere artikler fra (uundgåeligt A4-størrelse) tidsskrifter.

Endeligt kræver globaliseringen sin pris: Amerikanske virksomheder, der gør forretninger med myndigheder uden for USA (især EU), må konstatere, at de skal indsende forslag, tilbud, diagrammer osv. på A-formatpapir.

Søgning efter det rigtige filformat

Det er alt sammen godt og vel, men det løser ikke det umiddelbare problem: Hvordan kan man i dag sikre sig, at dokumenter, der skal bruges i Nordamerika og resten af verden, ikke fejler på grund af forskellene mellem papir i A4- og Letter-format?

Først, og med henvisning til alle de andre potentielle årsager til problemer, der er nævnt ovenfor, skal man ikke sende eller distribuere dokumenter, der er afhængige af eksterne faktorer for at blive vist og udskrevet korrekt. Så ingen Word-dokumenter, ingen Quark XPress-dokumenter, ingen PageMaker-filer, ingen AppleWorks-filer osv.

Selv om du er sikker på, at den person, der modtager dine filer, har den samme version af det samme program, alle de skrifttyper, du har brugt, og bruger den samme printer, er ingen af disse filformater sikre at sende på tværs af papirstørrelsesgrænserne. De fejler på dette sidste punkt, fordi de stadig er afhængige af eksterne faktorer for at blive vist og udskrevet.

For eksempel vil et Word-dokument, der er formateret med 25 mm margen på papir i Letter-størrelse, genstrøms den tekst, det indeholder, når det åbnes på en computer, der som standard viser dokumenter på A4. Selv ligefrem prosa, der kører i en enkelt kolonne, vil blive genudgivet under sådanne omstændigheder. Alt mere komplekst (f.eks. en blanding af tekst og billeder eller et manuskript) vil næsten helt sikkert blive vist forkert i den modtagende ende under sådanne forhold.

(Jeg vil endda gå så langt som til at foreslå, at det er udelukket at sende diskrete tekstfiler (dvs. en tekstfil, der sendes som en vedhæftet fil til en e-mail i stedet for at blive en del af selve meddelelsen), alene på grund af det stadig eksisterende problem med “hvilken linjeslutning har de brugt”, men det er et separat problem.)

Listen over dokumenttyper, der ikke må sendes, er temmelig lang. Listen over dokumenttyper, der kan sendes, er ret kort: rå PostScript-filer og Adobe Acrobat-filer (alias “pdf”-filer).

Både filformater koder og fastlægger de rumlige relationer mellem de enkelte elementer på en side. Det er relativt enkelt at generere rå PostScript-filer: indstil din computer til at udskrive til en PostScript-kompatibel printer (selv om du ikke har en til rådighed), og ‘udskrive’ derefter dit dokument til en fil. Den fil, der produceres på denne måde, er sikker at sende. Desværre kan filen ikke ses på en skærm, uden at man skal kaste sig ud i noget seriøst nørderi, og den kan kun udskrives pålideligt ved at sende den til en PostScript-kompatibel printer.

Acrobat-filer: det bedste af et dårligt parti

Hvilket som standard gør Acrobat-filer til den bedste løsning. Jeg siger “som standard”, fordi Acrobat-filer ikke ville være mit førstevalg. Filformatet er kun halvåbent, og Acrobat-filer er større, end jeg gerne vil have dem til at være i forhold til den mængde information, der er kodet i dem. Der er også det lille spørgsmål om omkostningerne.

Når man har købt et eksemplar af Word, koster det ikke mere at oprette et Word-dokument. Det samme gælder for andre værktøjer til oprettelse af dokumenter som Quark XPress, WordPerfect, PageMaker osv.

Men Acrobat markedsføres eller sælges derimod ikke som et værktøj til oprettelse af dokumenter. Adobe beskriver Acrobat som:

et universelt filformat, der bevarer alle skrifttyper, formateringer, grafik og farver i ethvert kildedokument, uanset hvilket program og hvilken platform der er anvendt til at oprette det

Grovt sagt er Acrobat en efterfølger til PostScript. Ligesom PostScript er Acrobat et programmeringssprog, der er designet til præcist at definere, hvor på en side objekter skal placeres. Acrobat indeholder også nogle til tider smarte værktøjer til at omdanne disse veldefinerede sider til formularer, der er i stand til at håndtere nye data i farten.

Fra en person, der ønsker at distribuere formaterede sider, er den vigtigste forskel mellem Acrobat og PostScript Adobe Acrobat Reader. Hvor Adobe tager penge for at inkludere en PostScript-fortolker i sine produkter (en del af grunden til, at PostScript-printere koster mere end ikke-PostScript-printere), er Acrobat-fortolkeren (dvs. Acrobat Reader) freeware, der kan downloades og indgår som en del af næsten alle køb af computere eller styresystemer.

Det lyder godt, indtil man skal oprette en Acrobat-fil og opdager, at Adobe blot har ændret, hvem de tager penge for. PostScript-filer er gratis at oprette (PostScript-printerdrivere er gratis), men det koster penge at se dem (PostScript-printere er dyre i forhold til ikke-PostScript-printere).

Acrobat-filer er gratis at se (Acrobat Reader er gratis), men det koster penge at oprette dem (ingen Adobe-værktøjer til oprettelse af Acrobat-filer er gratis).

Skabelse af Acrobat-filer

Adobe tilbyder flere værktøjer til at skabe Acrobat-filer, begyndende med en webbaseret tjeneste, som du kan prøve gratis og abonnere på for 10,00 USD/måned eller 100 USD/år. Denne tjeneste er kun tilgængelig for indbyggere i USA og Canada.

For resten af os (og for amerikanske og canadiske folk, der foretrækker en startpris frem for et løbende abonnementsgebyr) er der Adobe Acrobat, som Adobe tager 250,00 USD for, men som kan fås hos forhandlere for omkring 220,00 USD.

Adobe tilbyder også en række dyrere produkter i Acrobat-familien, der er designet til at opfylde behovene i virksomheders arbejdsgange.

Og for de eventyrlystne er der forskellige tredjeparter, der udnytter Acrobat’s semi-åbne karakter til at levere værktøjer til oprettelse af Acrobat uden Adobes formelle godkendelsesstempel. Et godt sted at begynde at grave efter oplysninger om sådanne værktøjer er The PDF Zone.

Forberedelse af filer til Acrobat

Så, med det endelige filformat besluttet og værktøjer til at skabe det pågældende format i hånden, er det tid til at beskæftige sig med dokumentlayoutet.

Ved første øjekast virker det relativt enkelt: begræns dine designs og layouts til et område, som begge størrelser kan rumme.

Hvis du lægger et A4- og Letter-papir oven på hinanden, så deres øverste venstre hjørne rører hinanden, er forskellen mellem de to ark tydelig: Letter er bredere end A4; A4 er længere end Letter. Så for at et design eller layout kan passe sikkert på begge arkstørrelser, må det ikke være bredere end A4 og ikke længere end Letter. Med andre ord: Grænserne for et design eller layout, der passer sikkert på begge sidestørrelser, er bredden på et A4-ark (210 mm eller 8,27″) og længden på et Letter-ark (11″ eller 279,4 mm). Desværre er det ikke helt så enkelt.

Tag et enkelt A4-ark, og anvend de standardmargener på 25 mm (ca. 1˝), som de fleste af os bruger, når vi udarbejder breve, rapporter, artikler og lignende. Arbejdsområdet – 160 mm x 247 mm – ligger godt inden for de grænser, der er nævnt ovenfor. Fyld dog siden med tekst, og der opstår et problem, hvis dokumentet sendes til en person, der bruger Letter. Det vil sige:

Teksten passer stadig på et enkelt US Letter-ark, men den løber ud over margenerne. Når en Letter-bruger udskriver filen, vil siden enten ikke blive udskrevet korrekt (fordi en del af teksten er placeret i en del af arket, der ikke kan udskrives), eller den vil blive udskrevet på en anden side. Det andet resultat er bedre, men ingen af delene er ønskværdige, og det andet er under alle omstændigheder afhængigt af for mange ukontrollable variabler.

For at undgå dette problem er den eneste mulighed for A4-brugere, der deler dokumenter med Letter-brugere, at øge deres nederste margener til 45 mm. Dette sikrer, at teksten på deres sider ikke kommer til at strække sig ind i no-go zonen, når den ses og udskrives af folk, der stadig bruger Letter. For igen at vise frem for at fortælle:

Ved skift til landskab er det Letter-brugere, der skal foretage justeringer af bundmarginen. Med en standardmargin på 25 mm på alle sider griber et landskabslayout, der ser fint ud på papir i Letter-størrelse, ind i fareområdet på A4:

Tilføj 6 mm ekstra (ca. 0.2˝) til den nederste margen, og problemet undgås:

De layouts, der er præsenteret i miniature ovenfor, er bevidst enkle, men de foreslåede marginændringer bør fungere selv med mere komplicerede gitterbaserede layouts. Der kan og vil dog opstå problemer med layouts, der er bygget op omkring en midterakse i stedet for et af de traditionelle gitre.

Et layout, der kun er bygget op omkring en midterakse, bør stadig kunne vises og udskrives på en acceptabel måde på tværs af papirstørrelser med passende marginjusteringer. En simpel plakat i victoriansk stil, f.eks. opstillet langs den lodrette akse i højformat:

Et nærmere eftersyn afslører et mindre visningsproblem. Designet er perfekt centreret på A4-arket, men er en smule excentrisk på den amerikanske brevside. En uundgåelig konsekvens af to ting: 1) A4 og US Letter er ikke lige brede, og 2) næsten alle værktøjer til at lægge og præsentere data digitalt bruger sidens øverste venstre hjørne som referencepunkt til at bestemme, hvor objekter skal vises på siden.

Sammenlignende problemer vil opstå med design, der er bygget op omkring den lodrette akse i landskabstilstand. Hvis selv disse mindre visuelle fejl er uacceptable, er der ikke meget andet at gøre end at udarbejde to versioner af et design (f.eks. en US Letter- og en A4-version eller en US Tabloid- og en A3-version). Design, der er bygget op omkring både den lodrette og vandrette midterakse, vil næsten helt sikkert under alle omstændigheder have brug for, at der udarbejdes både US- og ikke-US-versioner.

Og undgå problemet til at begynde med

Hvis alt dette virker som problemer, som du godt kunne undvære, så velkommen i klubben. Desværre er de eneste nuværende alternativer til at erkende og håndtere problemet:

1. Ignorere det og irritere og/eller miste kunderne hos folk, der bruger en anden sidestørrelse end dig.

2. overtale USA (og Canada) til at opgive deres forskellige imperiale målesystemer og gå helhjertet over til SI-systemet (eller det metriske system, for at bruge den mindre formelle betegnelse).

De fleste mennesker vil ende med at ignorere problemet. Det er kun en irriterende fejl i omgangsformen for folk, der deler dokumenter af ikke-kommercielle årsager, som for det meste tilgives eller i det mindste ikke kommenteres af den berørte part.

Og på trods af omfanget er det en almindeligt begået kommerciel fejl, fordi den tabte forretning skjules af den relative størrelse af de to store økonomier, der er berørt: USA og EU. En person, der opererer med succes i den ene sfære, kan ignorere den anden og ikke bemærke den tabte omsætning.

Med hensyn til det andet alternativ, og på trods af min dæmpede optimisme ovenfor, ser jeg ikke, at det sker i den nærmeste fremtid. Et skift ved lov (som det skete med succes i Australien i begyndelsen af 1974) er yderst usandsynligt, og den langsomme osmose af metriske betegnelser i det amerikanske liv har endnu ikke nået det stadium, hvor sådanne mål erstatter deres britiske ækvivalenter.

Dermed står vi tilbage, hvor vi startede: Vi har at gøre med to lidt forskellige papirstørrelser og alle de ulemper, der følger af forskellene.