I dagens indlæg vil du lære forskellen på primtal og sammensatte tal at kende. Derudover vil vi vise dig flere eksempler for at hjælpe dig med at forstå dem bedre.
Index
Hvad er primtal?
Primtal er de tal, der kun er delelige med sig selv og 1. Med andre ord, hvis vi forsøger at dividere dem med et andet tal, er resultatet ikke et helt tal. Så hvis man deler tallet med noget andet end 1 eller sig selv, får man en rest, der ikke er nul.
Primtal indtil 100
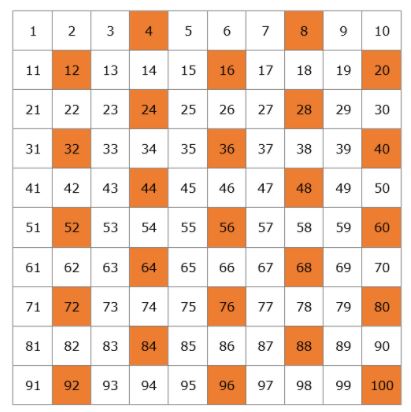
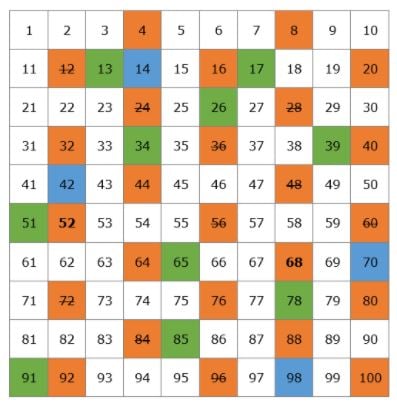
Vi skal lave en tabel med alle de primtal, der findes op til 100.
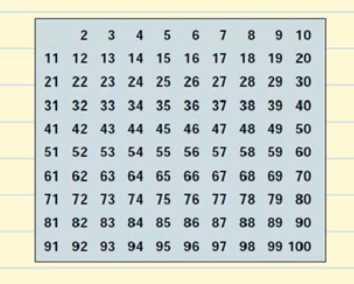
Lad os starte med 2. 2 er et primtal, men alle multipla af 2 vil være sammensatte tal, da de vil være delelige med 2. Vi streger alle multipla af 2 ud på tabellen.
Det næste primtal er 3, så vi kan strege alle multipla af 3 ud, da de vil være sammensatte tal.
Efter 3 er det næste primtal 5, så vi streger alle multipla af 5 over.
Derpå har vi primtal 7, og vi streger alle multipla af 7 over.
Det næste primtal er 11, så vi streger alle multipla af 11 over, som er 22, 33, 44, 55, 66, 77, 88 og 99. Alle disse tal var allerede blevet overstreget, så vi er færdige med at overstrege alle de sammensatte tal på vores tabel.

Dette er vores liste over primtal fra 1 til 100. Du behøver ikke at lære dem udenad, men det ville være bedst, hvis du husker de mindre tal, såsom 2, 3, 5, 7, 11, 13.
Hvor mange primtal er der?
Den græske matematiker Eratosthenes (3. århundrede f.Kr.) udviklede en hurtig måde at finde alle primtal op til et hvilket som helst givet tal på. Det er en proces, der kaldes Eratosthenes’ si.
Mærk dig, at der mellem 1 og 100 er 25 primtal. Hvor mange primtal er der i alt? Vi har siden oldtiden vidst, at der er uendeligt mange, så det er umuligt at opregne dem alle. Da Euklid, som var den første til at vise, at der var uendeligt mange i det 4. århundrede f.Kr., ikke kendte begrebet uendelighed, sagde han, at “primtal er flere end enhver fast mængde af dem”, hvilket betyder, at hvis du forestiller dig 100, er der flere, og hvis du forestiller dig en million, er der stadig flere.
Primtal 100 til 1.000
Lad os se på primtalene fra 100 til 1.000.

Vi beklager, at vi ikke kan vise dem alle, for som du ved, er der uendeligt mange. 😉
Primtal Eksempler på primtal
For at hjælpe dig med at forstå primtal bedre, vil vi forklare en øvelse.
Sara har 6 stykker slik, som hun gerne vil dele, men hun ved ikke, hvor mange personer hun kan dele dem med, så alle får den samme mængde, og der ikke er nogen tilbage. Hvor mange måder kan hun gøre det på?
Her er Sara og hendes 6 stykker slik:

Hvordan kan vi dele dem?
Den første og nemmeste måde er at give dem til én person, altså dividere med 1. På den måde får denne person 6 stykker slik.
Den næste mulighed er at dele dem mellem 2 personer. Da 6 divideret med 2 er 3, får hver person 3 stykker slik!

Vi fortsætter med det næste tal, 3. Hvis vi deler 6 stykker slik mellem 3 personer, er det også en nøjagtig deling, og hver person får 2 stykker slik:

Lad os fortsætte med tallene. Vi har ikke eksakte delinger med 4 og 5, men det har vi med 6.
Da 6 divideret med 6 er 1, kan vi give 6 børn 1 stykke slik hver.

Vi skal nu indsamle nogle oplysninger. Vi har 6 stykker slik, som vi kan dele (med en nøjagtig deling) mellem 1, 2, 3 og 6 personer. Med andre ord kan vi dividere tallet 6 og få 0 som rest, når vi deler det med 1, 2, 3 og 6. Disse tal er kendt som divisorer af 6.
Vi skal prøve med et andet tal, for eksempel 7.
Nu har Sara 7 stykker slik og vil gerne dele dem, men ved ikke, hvor mange personer hun kan dele dem med, så alle får den samme mængde, og der ikke bliver nogen tilbage. Hvor mange måder kan hun gøre det på?

Henry er så heldig! Han fik alle slikstykkerne!
Er der andre måder at gøre det på? Vi kan ikke dele 7 med 2, 3, 4, 5 eller 6, …men 7 er muligt!
Sara kan dele slikstykkerne mellem 7 personer og give dem et stykke hver:

Så 7 kan kun deles med 1 og 7, dets eneste divisorer er 1 og 7. Det er den type tal, vi kalder primtal.
Er der flere primtal? Selvfølgelig! Lad os kigge efter nogle flere:
- Er 4? Nej! Fordi dets divisorer er 1, 2 og 4.
- Er 5? Ja! Fordi dens divisorer er 1 og 5.
- Er 8? Nej! Fordi dets divisorer er 1, 2, 4 og 8.
Kort sagt, et tal er primtal, hvis det kun har 2 divisorer: 1 og sig selv.
Nu kan du søge efter masser af primtal!
Sådan finder du primtal
Vær meget opmærksom! Vi vil give dig et trick til at vide, om et tal er primtal eller ej, uden at du behøver at lede efter dets divisorer, men på en måde, der er sjovere og giver os divisorerne (hvis de har dem).
Lad os vælge et tilfældigt tal, 16 for eksempel.
For at tjekke, om det er et primtal eller ej, skal vi bruge en tabel, der minder meget om Montessori-kort til multiplikation. Og vi vil få lige så mange kugler som det tal, vi har valgt. I dette tilfælde 16 kugler.
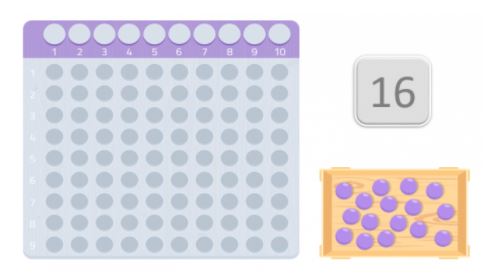
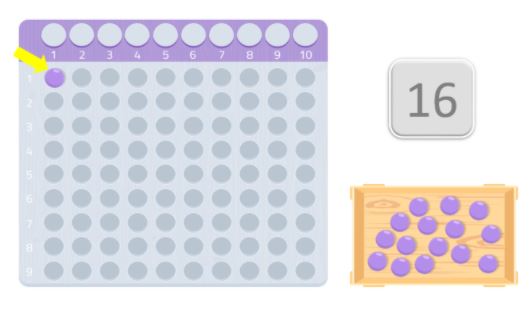
Når vi har bordet og kuglerne, skal vi placere dem på bordet og begynde med den første plads og forsøge at danne et rektangel. De tal, der udgør rektanglets kanter, er det pågældende tals divisorer.
Hvis det kun lykkes os at danne et rektangel med det samme tal, som vi bruger, og tallet 1, vil det være et primtal.
For eksempel placerer vi i dette tilfælde 8 kugler i den første række og yderligere 8 i den anden række. Som du kan se, har vi dannet et rektangel, og vi kan se, at 8, ligesom 2, er divisorer af tallet 16. Derfor er 16 ikke et primtal, for som du ved, er primtal de tal, der kun er delelige med sig selv og 1.
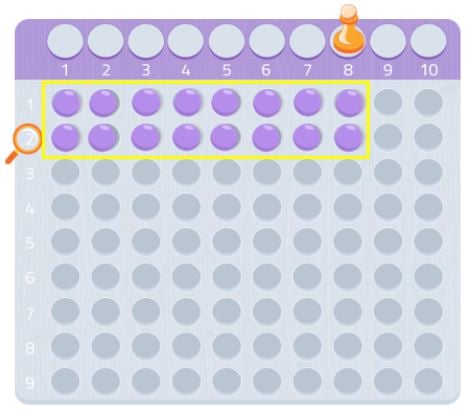
Vi kan prøve med et andet tal, f.eks. 7.
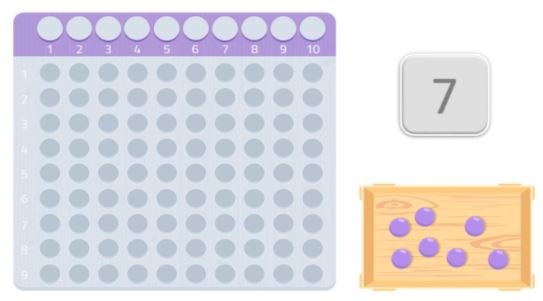
Som vi kan se, kan vi ikke lave et helt rektangel, vi ville mangle en kugle. Da vi ikke kan danne et rektangel, kan vi sige, at tallet 7 ikke har andre divisorer end sig selv og 1, som vi kan se på følgende billede:
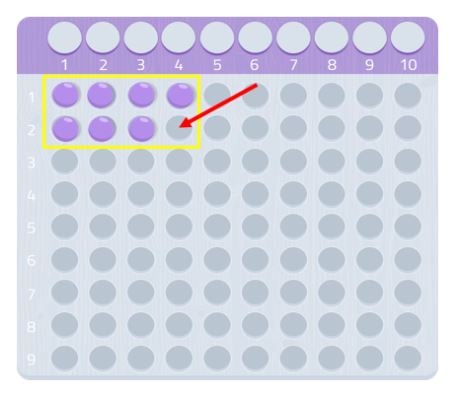
Derfor er 7 et primtal!
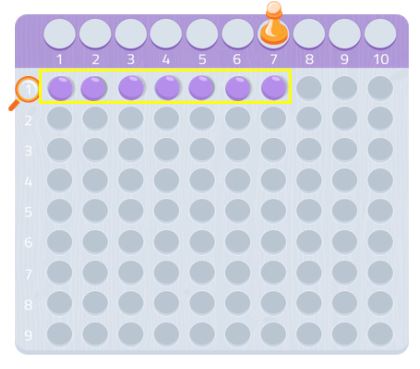
Prøv med et andet tal, så kan du se, hvordan det virker! Du kan bruge grapepapir og kigge efter rektangler, der bruger dette antal kvadrater.
Hvorfor er primtal vigtige?
Primtal er nøglen til aritmetik, nedenfor vil du se et eksempel, der viser deres betydning, ikke kun i matematik, men også i naturen.
Hvad mener vi, når vi siger, at primtal er nøglen til aritmetik?
Det skyldes, at ethvert tal består af et unikt produkt, der er sammensat af en serie af disse tal.
Det menes, at de har været studeret i omkring 20.000 år, da en af vores forfædre skrev en serie primtal (11, 13, 17 og 19) ned på Ishango-knoglen. Som om det var et tilfælde, er det blevet bekræftet, at de gamle egyptere arbejdede med dem for 4.000 år siden.
Dertil kommer, at naturen kender dem meget godt, og nogle arter har været i stand til at opdage dem i løbet af deres udvikling og drage fordel af dem for at overleve.
Jeg tænker på flere arter af cikader, f.eks. Magicicada septendecium, der lever i Nordamerika. Denne cikadeart har etableret sin ynglecyklus omkring 13 eller 17 år, ikke 12, 14, 15, 16 eller 18 – præcis 13 eller 17. Det gør det muligt for dem at undgå rovdyr, der også har periodiske reproduktionscyklusser; forestil dig et rovdyr med en 4-årig reproduktionscyklus.
Hvis en cikades livscyklus var 12 eller 14 år, ville den falde sammen med et rovdyr meget ofte, meget oftere end hvis den var 13 eller 17 år. Præcis 2 gange hvert 100. år, mens de ellers ville falde sammen i 11 cyklusser, hvilket ville bringe artens udvikling i fare.
Sikkerheden i elektronisk kommunikation er også baseret på primtal. Hver eneste krypteret meddelelse, der sendes over internettet (meddelelsesnetværk, køb eller elektroniske bankforretninger), har et stort tal tilknyttet, og det er meget vanskeligt at vide, hvor det er primtal eller ej. Modtageren har en af dets divisorer, og det er derfor, at de kan dekryptere det. Så det er afgørende for vores privatliv, når vi kommunikerer elektronisk, at vi har primtal.
Hvad er sammensatte tal?
Sammensatte tal er de tal, der er delelige med 1 og sig selv samt andre tal.
Vi skal se på et eksempel på et primtal og et sammensat tal.
11 kan skrives som multiplikationen 1 x 11, men det kan ikke skrives som nogen anden multiplikation af naturlige tal. Det har kun divisorerne 1 og 11, og derfor er det et primtal.
12 kan skrives som multiplikationen 1 x 12 og som multiplikationerne 3 x 4 og 2 x 6. Da 12 er deleligt med flere tal end 1 og sig selv, er 12 et sammensat tal.
Er 1 et primtal?
Der er folk, der tror det, fordi de siger, at 1 kun kan deles med 1 og sig selv, men i matematikken er tallet 1 blevet kasseret som et primtal, fordi det kun har én divisor. Faktisk bruges kriteriet “et positivt heltal er primtal, hvis det har præcis to positive divisorer” til at udelukke tallet 1 fra listen over primtal. Det er ikke fordi vi er kræsne med det, men hvis tallet et blev betragtet som primtal, ville mange matematiske egenskaber skulle siges anderledes.
Så, 1 er et sammensat tal?
Jamen, det er heller ikke sammensat, da det ikke kan sættes som et produkt af primtal. Tallet 1 er hverken primtal eller sammensat. Og før du spørger, så er nul heller ikke primtal eller sammensat, men det skyldes, at alle de overvejelser, vi forklarede for positive tal, altså større end nul.
Divisorer af et tal
Den divisor af et tal er den værdi, der deler tallet i eksakte dele, altså har en rest på 0.
Som eksempel skal vi beregne divisorerne for 24.
Vi begynder med at dividere med de mindste tal, der starter med 1.
Det næste tal er 6, men da vi allerede ved, at 6 er en divisor af 24, er vi færdige med at udregne divisorerne for 24.
Video: Faktorisering og primtal
Hvis du gerne vil vide mere om primtal og sammensatte tal, kan du tage et kig på følgende video. Du lærer også begrebet faktorisering ved hjælp af Montessoritabellen.
Denne video er en af vores interaktive tutorials, og selv om den ikke er interaktiv, kan du stadig se den så mange gange, som du har brug for, og dele den med dine venner. Hvis du gerne vil have adgang til vores interaktive tutorials, skal du registrere dig hos Smartick! Online-metoden, der hjælper børn i alderen 4 til 14 år med at lære og øve sig i matematik.
Hvis du gerne vil fortsætte med at lære om primtal og den bedste matematik tilpasset dit niveau, så registrer dig hos Smartick og prøv det gratis!
Lær mere:
- Primtal og sammensatte tal
- Primtal: Et trick til at hjælpe dig med at identificere dem
- Primtal: Lær hvordan du finder dem med Eratosthenes’ sigte
- Lær at faktorisere primtal
- Primtal Aktiviteter med Smartick



- Author
- Reneste indlæg
Et tværfagligt og multikulturelt team bestående af matematikere, lærere, professorer og andre fagfolk inden for uddannelse!
De stræber efter at skabe det bedst mulige matematiske indhold.
- Eksempler på matematiske ordproblemer i 3. klasse med løsninger – 25/03/2021
- Sammenhængende indvendige vinkler: Hvad de er, og hvordan man finder dem med eksempler – 03/11/2021
- Eksempler på ordproblemer for 2. klasse med løsninger – 02/04/2021