Man finder faktorialer overalt i kombinatorikken, fordi det er der, de stammer fra. Faktorialen blev skabt som en måde at udtrykke antallet af arrangementer af en gruppe af elementer, som vi naturligvis finder ved at bruge, i sin mest grundlæggende form, multiplikationsreglen for tælling.
Faktorialen er en slags uofficiel operation for multiplikationsreglen for tælling.
Hvorfor nulfaktorial er lig med 1
Det er her, det bliver svært, for hvis vi kun tænker på faktorialer i den sammenhæng, som de normalt er defineret, dvs.dvs. “produktet af alle positive hele tal mindre end eller lig med tallet”, så er det at finde ud af 0! som at støde ind i en mur.
De fleste vil fortælle dig, at 0! er defineret som 1, og hvis du spørger hvorfor, siger de bare “fordi det er defineret som 1”.
Ja, det er ret frustrerende. Det svarer matematisk set til at spørge dine forældre, hvorfor du skal følge en vilkårlig regel, som de har fundet på, og få at vide, “fordi jeg har sagt det.”
Men selv om det måske er en accepteret forældreteknik, er det en elendig måde at lære matematik på. Så hvad er problemet? Hvordan besluttede vi, at nulfaktorial er lig med et?
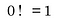
En intuitiv forståelse
Huskede du, at vi sagde, at faktorialet stammer fra den matematiske operation, der går ud på at finde antallet af permutationer eller arrangementer af en mængde? (Bemærk: ikke permutationerne af en mindre mængde fra en større mængde, men blot arrangementerne af en given mængde.)
Nul-faktorial kan opfattes som antallet af arrangementer af nul elementer i en mængde, også kaldet den tomme mængde {}. (Hvis du nogensinde har studeret mængder, måske i grundlæggende statistik eller diskret matematik, er du sikkert bekendt med begrebet tom mængde. Det er bogstaveligt talt mængden af ingenting.)
Hvis jeg nu spurgte dig, hvor mange arrangementer der er af én ting, ville du svare 1, fordi der kun er én måde at arrangere én ting på. Den samme idé følger her. Vores “én ting” er den tomme mængde, og antallet af arrangementer af den tomme mængde er ét. Det er det hele. Derfor er 0! lig med 1.
Sådan forenkler du faktorielle udtryk
Nu da vi har det grundlæggende bag os, er det tid til kernen i vores faktorielle tutorial: forenkling.
Den bedste måde at se matematik på er i praksis. Så her er jeg for at gå dig igennem de seks problemer, der er vist på billedet øverst i dette indlæg! Vi starter dejligt nemt, bevæger os derefter ind i kombinationsformlen med tal og derefter variabler og slutter af med nogle mere vanskelige faktorudtryk.
❤ BLIV FORBINDET ❤
Må ikke gå glip af et beat eller et matematisk problem!