ΔS kiszámítása termodinamikai ciklusokból
Az entrópia változását is kiszámíthatjuk egy termodinamikai ciklus segítségével. Amint azt korábban megtanultad, a moláris hőkapacitás (Cp) az a hőmennyiség, amely ahhoz szükséges, hogy egy anyag 1 moljának hőmérsékletét állandó nyomáson 1°C-kal megemeljük. Hasonlóképpen, a Cv az a hőmennyiség, amely ahhoz szükséges, hogy egy anyag 1 moljának hőmérséklete állandó térfogat mellett 1°C-kal emelkedjen. Az \(\PageIndex{2}\) ábrán az entrópia növekedése a hőmérséklet növekedésével megközelítőleg arányos az anyag hőkapacitásával.
Megjegyezzük, hogy az entrópiaváltozás (ΔS) és a hőáram (qrev) között a ΔS = qrev/T összefüggés áll fenn. Mivel qrev = nCpΔT állandó nyomáson vagy nCvΔT állandó térfogat mellett, ahol n a jelen lévő anyag mólszámát jelenti, az entrópia változása egy olyan anyag esetében, amelynek hőmérséklete T1-ről T2-re változik, a következőképpen alakul:
\
Amint azt az itt előírtnál haladóbb matematikaórákon meg fogod tapasztalni, megmutatható, hogy ez a következővel egyenlő:A természetes logaritmusok áttekintését lásd a 11. fejezet “Folyadékok” című 6. alapvető készségében.
\
Hasonlóképpen,
\
Így használhatjuk a hőkapacitás mérések (18.20. egyenlet vagy 18.21. egyenlet) és a fázisátalakulás esetén a fúziós vagy gőzölési entalpiák kísérletileg mért értékeinek kombinációját (18. egyenlet.18), hogy kiszámítsuk a minta hőmérsékletváltozásának megfelelő entrópiaváltozást.
Az entrópiaváltozás kiszámításához használhatunk termodinamikai ciklust, ha egy anyag, például a kén fázisváltozása nem mérhető közvetlenül. Amint azt a 6. példa feladatában megjegyeztük, az elemi kén két formában létezik (\(\PageIndex{3}\) ábra a) része): egy orthorombikus, erősen rendezett szerkezetű formában (Sα) és egy kevésbé rendezett monoklin formában (Sβ). Az orthorombikus (α) forma szobahőmérsékleten stabilabb, de 95,3 °C (368,5 K) feletti hőmérsékleten fázisátalakuláson megy át a monoklin (β) formába. Az Sα-ból Sβ-be történő átmenetet a \(\PageIndex{3}\) ábra b) részében látható termodinamikai ciklussal lehet leírni, amelyben a folyékony kén egy köztes állapot. A folyékony kén Sβ-vé történő átalakulását kísérő entrópiaváltozás (-ΔSfus(β) = ΔS3 a ciklusban) nem mérhető közvetlenül. Mivel azonban az entrópia egy állapotfüggvény, ΔS3 kiszámítható az Sα-Sβ átmenet teljes entrópiaváltozásából (ΔSt), amely egyenlő a termodinamikai ciklus lépéseihez tartozó ΔS értékek összegével, a 18. egyenlet segítségével.20 és a táblázatban szereplő termodinamikai paraméterek (az Sα és az Sβ hőkapacitása, ΔHfus(α) és az Sα olvadáspontja.)

A ΔS3 feloldása -3,24 J/(mol-K) értéket ad. Ahogy az egy kevésbé rendezett állapot (folyadék) rendezettebbé (kristály) való átalakulása esetén várható, ΔS3 negatív.
Hogyan mérik az entrópiát
Az anyag abszolút entrópiáját 0 K feletti bármely hőmérsékleten úgy kell meghatározni, hogy kiszámítjuk a q hőmennyiség növekedését, amely ahhoz szükséges, hogy az anyag 0 K-ról a kívánt hőmérsékletre kerüljön, majd a q/T arányokat összegezzük. Kétféle kísérleti mérésre van szükség:
- Az anyag által a kérdéses hőmérséklettartományon belül végbemenő fázisváltozásokhoz kapcsolódó entalpiák. Egy szilárd anyag olvadása és egy folyadék elpárolgása a hőenergia felvételére rendelkezésre álló mikroállapotok számának jelentős növekedésének felel meg, így ahogy ezek a folyamatok végbemennek, energia áramlik a rendszerbe, feltöltve ezeket az új mikroállapotokat az állandó hőmérséklet (a fagyási vagy forráspont) fenntartásához szükséges mértékben; ezek a beáramló hőenergiák megfelelnek a fúziós és a párolgási hőnek. Az olvadáshoz kapcsolódó entrópianövekedés például egyszerűen ΔHfúzió/Tm.
- Egy fázis C hőkapacitása azt a hőmennyiséget fejezi ki, amely a hőmérséklet ΔT kis mértékben, pontosabban egy végtelenül kis dT mennyiséggel történő megváltoztatásához szükséges. Így egy anyag felmelegedése által okozott entrópianövekedést egy fázisátalakulást nem tartalmazó hőmérséklet-tartományban a C dT/T mennyiségek összegével adjuk meg minden egyes dT hőmérséklet-emelkedés esetén. Ez természetesen csak az integrál
\
Mivel a hőkapacitás maga is kissé hőmérsékletfüggő, az abszolút entrópiák legpontosabb meghatározásához a fenti integrálban a C konstans C helyett a C T-től való függését kell használni.
\
Ha ez nem ismert, akkor egy sor hőkapacitásmérést végezhetünk ΔT szűk hőmérsékleti lépcsőkön, és megmérhetjük a görbe egyes szakaszai alatti területet.
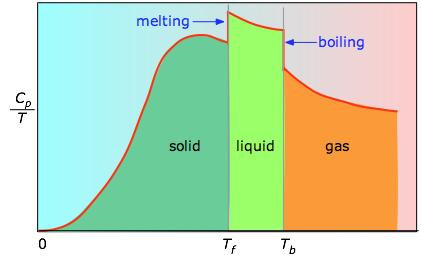
A grafikon egyes szakaszai alatti terület az anyag ΔT intervallumon keresztül történő melegítésével járó entrópiaváltozást jelzi. Ehhez hozzá kell adni az olvadás, a párolgás és az esetleges szilárd-szilárd fázisátalakulások entalpiáit. A Cp értékeit a nulla közeli hőmérsékletekre nem mérik közvetlenül, hanem kvantumelméletből becsülhetők.
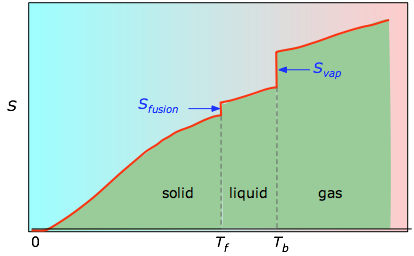
A 0 K-tól bármely adott hőmérsékletig terjedő kumulatív területeket (a bal oldali kísérleti diagramból) ábrázoljuk a T függvényében, majd a fázisváltozási entrópiákat, mint például Svap = Hvap / Tb, összeadjuk, hogy megkapjuk az abszolút entrópiát a T hőmérsékleten.