ロジスティック方程式

ロジスティック方程式（Verhulst model、logistic growth curveとも呼ばれる）はピエール・ベルホルスト（1845、1847）が最初に発表した人口増殖のモデルである。 このモデルは時間的に連続であるが、連続式をロジスティック写像と呼ばれる離散的な二次漸化式に修正したものも広く用いられている。

連続版のロジスティックモデルは微分方程式

(1)

ここではマルサスのパラメーター（最大人口増加率）、はいわゆる環境収容力（＝。 最大持続可能人口）である。 両辺をで割ってとすると、微分方程式

(2)

で知られているように、この微分方程式は をロジスティック方程式と呼び、解

(3)

関数はシグモイド関数と呼ばれることもある。

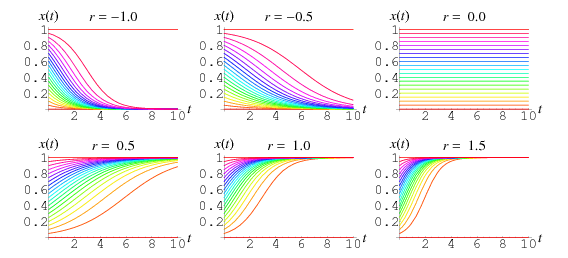
通常は正の値に拘束されますが、上記の解のプロットはの様々な正と負の値、初期条件は0.00から1.00まで0.05刻みで示したものです。

ロジスティック方程式(3)の離散版はロジスティック写像と呼ばれる。

(4)

から得られる曲線はロジスティック曲線と呼ばれることもある。 同様に、式(3)を正規化した形は、ロジスティック分布として知られる統計分布としてよく使われます。

。