不規則な多角形の面積

この記事は、私がオンラインで過度に複雑な方法で説明されているのを見つける幾何学的な問題への簡単な解決策を説明します。 問題は、部屋の間取り図や土地など、2次元の閉じた図形（「不規則多角形」）の面積と周囲長を計算することで、どんなに複雑でもかまいません。 ガウスの時代から、あるいはそれ以前からバージョンは存在していました。 しかし、ほとんどのオンライン記事では、不必要に複雑な方法でこの方法を説明しています。 Wikipedia の靴ひもの公式の記事、Polygon の記事で同様に複雑な方法、そして、この方法の最も複雑でない実施形態を提供するよりも、著者の博識を示すために計算されたように見える多くの記事などが参照されています。 この記事 (PDF) では、最も複雑ではない (しかし決して単純ではない) 式の 1 つを示しています:

(1) $A = \frac{1}{2} \x_0 & x_1 \ y_0 & y_1 \황right| + \left|begin{array}{cc} x_1 & x_2 \ y_1 & y_2 } 황end{array} 황right| + \left|begin{array} {cc} x_1 & x_2 \ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ \⑭+… + \left|jabegin{array}{cc} x_{n-2} & x_{n-1} \ y_{n-2} & y_{n-1} {end{array}} \right| + \left|begin{array}{cc} x_{n-1} & x_0 \ y_{n-1} & y_0

Where $x_n,y_n$ is polygon vertex expressed in Cartesian coordinates, $emptyleft|begin{array}{cc} x_0 & x_1 \ y_0 & y_1 \ end{array} \この方法は、数学的な背景を理解するよりも、使う方が簡単です。 この記事を書いている間、私は生徒からの質問に対する答えがあまりにも複雑で、生徒を啓発することができないようなものをいくつも発見しました。 この記事では、この方法をできるだけシンプルでわかりやすくするために、できる限りのことをするつもりです。

Computing Area and Perimeter

この方法は、アルゴリズムとして最も簡単に表現されます。

• 不規則多角形の頂点は直交座標で表すことができます。 x,y$。
• 各座標のペアは、次のような面積和アルゴリズムで処理されます。
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …となります。

• 上記を簡単に数式で表すと。
  

  (2) 不規則多角形の面積 $displaystyle A = \frac{1}{2}. \sum_{i=m}^{n-1}{x_{i+1} \ãÔßæÑ ãÔßæÑ ãÔßæÑ \Όταμμα για για για για για για για για για για για για για για για για για για για για για για για για για βια βια βια για για βνη 土地の調査では、フィールドデータが図を閉じる、つまり、最後の項目が最初の項目と同じになるようにする必要があります。 このようなアプリケーションでは、式(1)のように自動的に図を閉じてしまうと、評価する必要のあるエラーが隠れてしまう。 そのような目的のために、処理中にトラバースの最後に最初のデータ項目を再評価するか、最後のデータとして最初のデータ項目を繰り返すデータセットを提供するだけでよい。

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• 上の “array” は直交座標 $x,y$ 、つまり座標の集合を意味するものであり、この引数には次のようなものが含まれます。e. ((10,10),(10,20),(20,20),(20,10),(10,10)). このデータセットについて、最初のデータ項目が最後に繰り返されていることに注意してください。

• ここで、面積と周囲長の両方を計算する少し複雑なPython関数を紹介します。
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• 再び、この注意事項です。 上記のコード例のいずれにおいても、土地測量データ削減以外の用途では、提供されたデータセットには、最初のデータ項目のコピーを最後のデータとして含めるべきである、すなわち。

• これらの例に Python を選んだのは、Python のリストがつまらないものを最小限に抑えながら、アルゴリズムの意味を最大化するためです。 複素数をサポートしていない言語では、次の方法で外周の結果を作成することができます。 p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

形式的には、周囲長はベクトルの大きさの合計である。

(3) 周囲長 $displaystyle P = \sum_{i=m}^{n-1}{sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-) }}

周囲長はベクトルの大きさの和である。y_i)^2}$

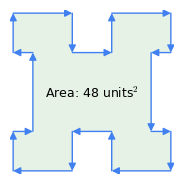
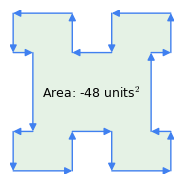図1.図2.1: 時計回り vs.

• 多角形の中で選んだ原点は面積や周囲長の計算には関係なく、図形が閉じていることだけが重要である。
• 「時計回りの法則」： ベクトルの順序は重要で、外周を時計回りに横切ると面積の結果は正になり、反時計回りだと負になる (図 1)。 図 1 のような複雑な図形から屈折の面積を差し引くのは、このメソッドの特性です。「屈折」は、ポリゴン内で反時計回りにトラバースすることを表します。
• このメソッドの多くのアプリケーションでは、極ベクトルからなる元のデータ ソース (土地調査の法的記述などが例) を使用しますが、この方法ではデカルトが必要です。 極座標からデカルト座標への変換は簡単ですが、この要件を覚えておくことが重要です。
• 繰り返しになりますが、正確な面積計算のためには、記述された多角形は閉じた図形でなければならず、最後の座標は最初の座標と等しくなければなりません。 長さベクトルからなるフィールド データを使用して、その後デカルト形式に変換するアプリケーションでは、開始と終了のデカルト座標を比較することをお勧めします (これらは等しくなければなりません)。 たとえば、古い土地調査 (安価なコンピュータ能力の時代以前) では、通常このテストに失敗します。

Area/Perimeter Computer

このセクションでは、完全に機能する面積/周囲長コンピュータで、入力したデカルトまたは極座標データペア、あるいは測量法的記述を処理することが可能です。 データの種類（デカルトx,y座標、極m,θ座標、測量法記述）を選択し、下のデータ入力エリアにデータを入力（またはペースト）するだけです。

ブラウザーのセキュリティーの問題から、過剰な入力を避け、他のソースから大量のデータをインポートするために、読者はシステムのクリップボードを使用する必要があります。 ソース アプリケーションでデータをクリップボードにコピーし、下のデータ入力領域をクリックして、Crtl+A ですべて選択、Ctrl+V で他の場所からデータをペース、Ctrl+C で自分の入力したデータをコピーするだけでよいのです。

Cartesian (x,y)

polar (m,θ)

Survey description

Data Entry Areaを選択します。 すべて選択します。 Ctrl+A｜コピーします。 Ctrl+C｜貼り付け。 Ctrl+V

Chart Area:

Sorry – your browser does not support the graphic ability this feature requires –
consider install Google Chrome or Firefox.

オプション：

ライン

矢印

起点

中心

長さの単位。

線幅：

反転

結果：すべて選択。 Ctrl+A｜コピーします。 Ctrl+C｜貼り付け。 Ctrl+V

入力データの種類

面積/周長コンピュータは3つの入力モードがあります：

• 直交座標（x、y）の組です。

  • 各座標は水平(x)と垂直(y)の部分を持つ2次元位置(デカルト座標)です。
  • 座標は累積しない – それぞれ独立してその位置を記述する。
  • つまり正方形はこうなる。
    • 0,0 (原点)
    • 0,100 (上)
    • 100,100 (右)
    • 100,0 (下)
    • 0,0 (原点復帰)

    
    ＜5228＞図2.正方形は次のようになる。 コンパスローズ

上の例のカンマは、読者のためにデータペアをグループ化するためだけのもので、エリアコンピュータのデータパーサーには何の意味もない。

パーサーは十分に堅牢で、上記の例をコンピュータのデータ入力エリアに貼り付けても動作します（試してみてください）。

唯一の制限は、説明用のコメントに数字を含めることができないことです。

• 各座標は距離と角度 (極ベクトル) からなります。
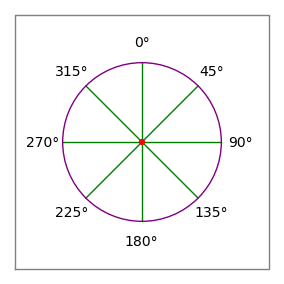
• 角度はコンパスの慣習に従っており、0度は上または「北」、90度は右または「東」 (図 2) です。
• 以前のデカルト形式とは異なり、これらの座標は累積です – 各新しいベクトルが現在位置に追加されます。
  • 100,0 (up)
  • 100,90 (right)
  • 100,180 (down)
  • 100,270 (back to the origin)
• この例は、以前と同様に、コンピューターのデータ入力領域に貼り付けて極モードを選択すれば動作します。
• 極座標の注意点として、原点は暗黙的にx = 0, y = 0にプリセットされています。

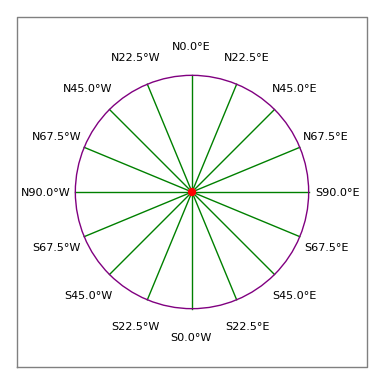図3：測量士のコンパスローズ

法律上の記述です。

• まず、「長さの単位」選択と結果表示の関係について説明します。
  • 各ポリゴンについて、共通の面積単位（フィート2、メートル2など）の固定セットを使用して、面積結果のリストが計算されます。
  • 直交および極座標モードでは、データエントリーに単位がないため、ユーザーが長さに割り当てる単位を選択します。
  • 測量モードでは、法的記述に長さの単位（フィート、メートルなど）が含まれており、長さの単位はソースによって事前に定義されていることを意味します。 したがって、ユーザーが長さの単位を変更すると、面積値ではなく長さのラベルと値が変更されます。
• 測量記述パーサーは、3 つのデータ解析方法の中で圧倒的に信頼性が低く、堅牢なデータ変換方法というよりは実験的なものです。
• 私は、多数の法的な説明文 (上記の計算機で例として提供されている) をダウンロードし、すべてが正常にデコードできるまでパーサーのコードをチューニングして、このパーサーを作成しました。

「成功」の基準は、結果が説明文の主張と同じ平方面積を持っており、図形が「閉じる」ことです。

• 測量作業では、測量の終点と始点がどの程度一致しているかを表すために「クロージャー」、特に「クロージャーの誤差」という用語が使われることがあります。 これは現実にはほとんど当てはまりません。クロージャーの誤差は通常、現地作業の誤差から生じますし、安価なコンピュータが登場する前に発行された古い測量では、クロージャーがかなり悪く、また正方形の面積の推定が非常に不正確な傾向にあります。
• 測量の法的記述は、土地のプロットを記述する正式な方法です。その形式と構文は、測量士によって共有される、多少任意で受け入れられた慣習によって、何十年もかけて生み出されました。 その必須要素とは
  • 説明されている区画の寸法を説明する内容からいくつかの予備的な内容を分離する、「開始点」というフレーズの存在です。 ある文書は “True point of beginning “と言い、ある文書は “Real point of beginning “と言い、ある文書は “Point of beginning “と言う。 成功したパーサーは、このフレーズの前のコンテンツを削除し、それ以降のすべてを保持する必要があります。
  • 測量士が使用する特殊な極ベクトルを記述する一連のフレーズです。
    • 単語 “North” か “South” またはその省略形 “N” か “S”。
    • 次に度、分、秒単位で表される角度を表す。
    • 次に距離。
    • 次に距離単位-フィート、メートルなど。
  • 以下は、サンプル法的記載事項からの測量者ベクトルのいくつかの異なる例です。
    • N 2°0’0″ W – 63.50 feet
    • N90°00’00 “W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.0 FEET.86 feet
    • S. 22 degrees 41′ 55″ E. 174.10 feet
  • Notice about the above examples that they all have different syntax.上記の例は、すべて異なる構文を持っています。 このパーサーがうまくデコードできない法的な記述はたくさん存在しますが、それは私がそれらの構文を取り込もうとしなかったからに過ぎません。 しかし、存在する多数の法的記述のための真に堅牢なパーサーは、Watson のように賢くなければならないことを付け加えておきます。
  • この領域/境界線コンピュータのユーザーは、プレーン テキストの法的記述を送信してパーサーがそれを理解することを希望しないほうがよいかもしれません。 直接手で入力する (またはインポートするためにトラバースのリストを他の場所で作成する) には、この規約を使用します。
    • 許容されるトラバース入力は、単語 “North” か “South” か文字 “N” か “S”、角度の度、分、秒を示す最大3つの数字、単語 “East” か “West” か文字 “E” か “W” 、距離、距離単位で構成されていることに留意してください。
    • したがって、許容できる入力は “N 30 15 45 W 100 feet” となり、北の西30度15分45秒を指す100フィートのトラバース（すなわち、およそ330コンパス度、図3を参照）を意味することになる。
    • 分と秒のエントリは、それらがゼロに等しい場合、またはエントリが十進の度、または度と十進の分である場合、スキップされるかもしれません。
  • 印刷された法的記述をこのようなエントリに変換することは難しくなく、誤りを検出する方法はいくつもあります。 すべてのトラバースを入力した後、図に閉鎖エラーがなく、オリジナルと同じ平方面積を報告している場合、エントリが正しい（またはオリジナルの記述と同じエラーを持っている）可能性があります。
  • この方法で法的記述を入力後、許容できない閉鎖エラーがあるか、平方面積が間違っている場合は、元のデータが間違っている可能性があることを思い出してください。

Note

Cartesian (x,y) examples を見ながら、異なる形状の面積と周長の比に注意してください。 異形の多角形」は中間の比率、「円」は最も小さい比率、そして「ヒルベルト空間」は圧倒的に大きい比率を持つ。 この関係は高次元にも及び、球は表面積あたりの体積が最も大きいことが知られている。

円の例について-それは「単位円」、半径が1の円である。 提供された例では、面積は $JPI$ に、周囲は $2JPI$ に近似しており、単位円としては正しい値です。 この値が近似値ではなく、正確に$83pi$と$83pi$になるためには、多角形の辺の数が無限でなければならない。 私はこれを断念しました。 🙂

ヒルベルト空間の例は、（あまり多くのデータを生成しないように）適度な次数の選択でSageアルゴリズムを使って生成しました。 原理的には、ヒルベルト空間は、2 次元では面積に対する周囲長、3 次元では体積に対する表面積の比が無限になりえます。 ヒルベルト空間がどれほど複雑になるかを見るには、ここをクリックして次数7のヒルベルト空間をご覧ください。

Hilbert の例について、計算された面積が 1×1 の表面に対して 1/2 に近いことに注意してください。 理想的には、線図形を面積図形に変換する必要がなく、正しいアルゴリズムがあれば、表面積は同じ寸法の正方形のちょうど 1/2 になる。

極入力モードは、0度を「上」、90度を「右」などに置き換え、それぞれの旋回と移動シーケンスを一つのコマンドに折り畳めば、Turtle グラフィックとほぼ同等になる。 極入力モードを使用すると、距離と角度が直交座標よりも簡単に追跡できるので、複雑な形状を手作業で構築する簡単な方法です。

私が最初に上記の土地測量面積計算方法を使ったのは、オレゴン州の田舎に住んでいたときで、自分の所有地の面積と周囲を知る必要がある人たちに囲まれていました。 不動産屋が、事実を知るすべもない人々を堂々とだますという、ショッキングな事例にたくさん遭遇しました。 何度も法的な記述から面積を計算したのですが、保証証書のエーカー数に関する主張がひどく不正確で、常に現実よりも高いことが判明したのです。 私は新しく手に入れた Apple II (現代の鉛筆削りのような処理能力) を持っていたので、これは非常に簡単でした。しかし、作業しているうちに、総エーカー数が約 3 エーカー、全体の約 25% もずれていることに気づきました。 私は権利会社に問いただしましたが、権利会社は図々しく「ここを見てください、証書には “more or less” と書いてありますよ」と答えました。

別の機会に私は土地の購入を始めましたが、上記の経験から警戒して、権利証券を受け取ったときに私はその法的記述をプログラムに入力して、地積請求が正確かどうかを確認しようと決めました。 ところが恐ろしいことに、その区画のすべてのタイトルポリシーが、最初に測量された土地の法的記載と同じであることがわかったのです。 その土地開発会社は、売り出された何十もの区画のうちのひとつだけを測量してお金を節約し、その法的記述をすべての権利書に記載することにしたのだ。 結局のところ、誰が数学について何も知らないのです。

権利会社と開発業者と議論し、法的記述が丁寧な虚構でないように調査費用を支払うよう説得しようとした後、私は諦めてその土地を購入しないことにしました。

Version History

• 2013.04.15 Version 1.3.XXXXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX.XXX. デフォルトのデータ形式、つまり最初のデータポイントを最後として繰り返すリストについての詳細な説明を追加。 測量記述パーサをさらに最適化し、より多くの結果データフィールドを追加しました。
• 2013.03.23 Version 1.1. より多くの種類の記述を扱うために法的記述パーサを改善し、長さ単位のセレクタと共通単位での面積の結果リストを追加しました。
• 2013.03.22 Version 1.0. 初期公開リリース。