熱力学サイクルからのΔSの計算
熱力学サイクルによるエントロピー変化の計算も可能です。 前回学習したように、モル熱容量(Cp)とは、ある物質1molの温度を定圧で1℃上げるのに必要な熱量のことである。 同様に、Cvは体積が一定のときに1molの物質の温度を1℃上昇させるのに必要な熱量である。 図中の温度上昇に伴うエントロピーの増加は、物質の熱容量にほぼ比例します。
エントロピー変化(ΔS)は、熱流(qrev)に対してΔS=qrev/Tで関係付けられることを思い出してください。 qrev = nCpΔT at constant pressure or nCvΔT at constant volume, where n is the number of moles of substance present, the change in entropy for a substance whose temperature changes from T1 to T2 is follows:
ここで求められているよりも上級数学コースで発見するように、これが以下に等しいことが示される。自然対数の復習は、11章「液体」必須スキル6を参照せよ。
同様に、
したがって、熱容量測定(式18.20または式18.21)および相変化が含まれる場合は融合または蒸発のエンタルピーの実験測定値の組み合わせ(式18.18)を用いて、試料の温度変化に対応するエントロピー変化を計算することができる。
硫黄などの物質の相変化を直接測定できない場合、熱力学的サイクルを用いてエントロピー変化を計算することができる。 例題6の演習で述べたように、元素状硫黄は規則性の高い斜方晶系(Sα)と規則性の低い単斜晶系(Sβ)の2つの形態(図中(a)部分)で存在する。 斜方晶系は室温ではより安定であるが、95.3℃(368.5K)以上で単斜晶系に相転移する。 SαからSβへの相転移は、液体硫黄を中間体とした図(b)の熱力学的サイクルで記述することができる。 液体硫黄のSβへの変換に伴うエントロピーの変化(サイクルでは-ΔSfus(β)=ΔS3)を直接測定することはできませんが、液体硫黄のSβへの変換に伴うエントロピーの変化(サイクルでは-ΔSfus(β)=ΔS3)を測定することができます。 しかし、エントロピーは状態関数であるため、ΔS3は、熱力学的サイクルのステップのΔS値の合計に等しいSα-Sβ遷移の全体のエントロピー変化(ΔSt)から、式18を用いて計算することができる。20と熱力学パラメータ(SαとSβの熱容量ΔHfus(α)、Sαの融点)

ΔS3を解くと-3.24J/(mol-K)の値が得られる。
エントロピーの測定方法
0K以上の任意の温度における物質の絶対エントロピーは、その物質を0Kから目的の温度まで持っていくのに必要な熱の増分qを計算し、その比率q/Tを合計することによって決定しなければならない。
- 目的の温度範囲内で物質が受ける可能性のあるあらゆる相変化に関連するエンタルピーを測定する必要がある。 固体の融解と液体の気化は、熱エネルギーを受け入れることができる微小状態の数の大幅な増加に相当するため、これらのプロセスが発生すると、エネルギーが系に流れ込み、一定の温度(凝固点または沸点)を維持するために必要な程度にこれらの新しい微小状態を満たします。 たとえば、融解に伴うエントロピーの増加は、ちょうどΔHfusion/Tmです。
- ある相の熱容量Cは、温度をわずかΔT、より正確には無限小の量dTだけ変化させるために必要な熱量を表します。 したがって、相転移を伴わない温度範囲で物質を温めたときのエントロピーの増大は、温度dTの増加ごとにC dT/Tの総和で与えられる。 これはもちろん積分
熱容量はそれ自体わずかに温度に依存するので、絶対エントロピーを最も正確に決定するには、上記の積分で定数Cの代わりにCの温度に対する関数依存性を使用する必要があります。
これがわからないときは、狭い温度増分ΔTにわたって一連の熱容量測定を行い、曲線の各セクションの下の面積を測定すればよい。
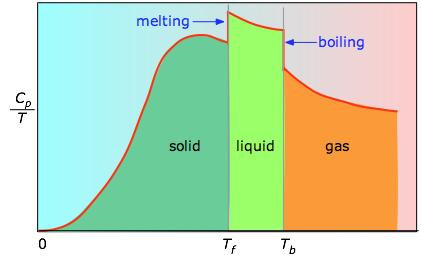
プロットの各セクション下の領域は、間隔ΔTで物質を加熱したときのエントロピーの変化分を表します。 これに融解、気化、固液相転移のエンタルピーを加えなければならない。 Cpはゼロ付近の温度では直接測定できないが、量子論から推定できる。
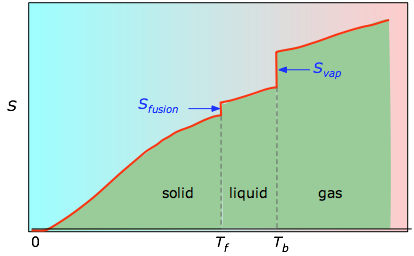
0Kから任意の温度までの累積面積(左の実験プロットから取得)をTの関数としてプロットし、Svap = Hvap / Tbなどの相変化エントロピーを加算して温度Tでの絶対エントロピーを求めたものです。