Obliczanie ΔS z cykli termodynamicznych
Możemy również obliczyć zmianę entropii używając cyklu termodynamicznego. Jak dowiedziałeś się wcześniej, molowa pojemność cieplna (Cp) to ilość ciepła potrzebna do podniesienia temperatury 1 mola substancji o 1°C przy stałym ciśnieniu. Analogicznie, Cv to ilość ciepła potrzebna do podniesienia temperatury 1 mola substancji o 1°C przy stałej objętości. Wzrost entropii wraz ze wzrostem temperatury na rysunku jest w przybliżeniu proporcjonalny do pojemności cieplnej substancji.
Przypomnijmy, że zmiana entropii (ΔS) jest związana z przepływem ciepła (qrev) przez ΔS = qrev/T. Ponieważ qrev = nCpΔT przy stałym ciśnieniu lub nCvΔT przy stałej objętości, gdzie n to liczba moli obecnej substancji, zmiana entropii dla substancji, której temperatura zmienia się z T1 do T2 jest następująca:
Jak odkryjesz na bardziej zaawansowanych kursach matematyki niż te, które są tutaj wymagane, można wykazać, że jest to równe następującej zależności:Aby zapoznać się z logarytmami naturalnymi, zobacz Podstawowe umiejętności 6 w rozdziale 11 „Ciecze”.
Podobnie,
Więc możemy użyć kombinacji pomiarów pojemności cieplnej (Równanie 18.20 lub Równanie 18.21) i doświadczalnie zmierzonych wartości entalpii syntezy lub parowania, jeśli mamy do czynienia z przemianą fazową (Równanie 18.18) do obliczenia zmiany entropii odpowiadającej zmianie temperatury próbki.
Możemy użyć cyklu termodynamicznego do obliczenia zmiany entropii, gdy zmiana fazy dla substancji takiej jak siarka nie może być zmierzona bezpośrednio. Jak zauważono w ćwiczeniu w Przykładzie 6, siarka elementarna występuje w dwóch formach (część (a) na Rysunku): forma ortorhombiczna o wysoce uporządkowanej strukturze (Sα) i mniej uporządkowana forma monokliniczna (Sβ). Forma ortorhombiczna (α) jest bardziej stabilna w temperaturze pokojowej, ale ulega przemianie fazowej do formy monoklinicznej (β) w temperaturach wyższych niż 95,3°C (368,5 K). Przejście z Sα do Sβ może być opisane cyklem termodynamicznym pokazanym w części (b) na rysunku, w którym ciekła siarka jest fazą pośrednią. Zmiana entropii towarzysząca przemianie ciekłej siarki w Sβ (-ΔSfus(β) = ΔS3 w cyklu) nie może być mierzona bezpośrednio. Ponieważ jednak entropia jest funkcją stanu, ΔS3 można obliczyć z całkowitej zmiany entropii (ΔSt) dla przemiany Sα-Sβ, która jest równa sumie wartości ΔS dla poszczególnych etapów cyklu termodynamicznego, korzystając z równania 18.20 i tabelarycznych parametrów termodynamicznych (pojemności cieplne Sα i Sβ, ΔHfus(α), oraz temperatura topnienia Sα.)

Rozwiązanie dla ΔS3 daje wartość -3,24 J/(mol-K). Zgodnie z oczekiwaniami dla przemiany stanu mniej uporządkowanego (ciecz) w bardziej uporządkowany (kryształ), ΔS3 jest ujemna.
Jak mierzone są entropie
Antropia bezwzględna substancji w dowolnej temperaturze powyżej 0 K musi być określona przez obliczenie przyrostów ciepła q potrzebnych do doprowadzenia substancji z 0 K do temperatury zainteresowania, a następnie zsumowanie stosunków q/T. Potrzebne są dwa rodzaje pomiarów doświadczalnych:
- Entalpie związane z wszelkimi przemianami fazowymi, jakim może ulegać substancja w interesującym nas zakresie temperatur. Topnienie ciała stałego i parowanie cieczy odpowiadają znacznemu wzrostowi liczby mikrostanów dostępnych do przyjęcia energii cieplnej, więc w miarę zachodzenia tych procesów energia będzie napływać do układu, wypełniając te nowe mikrostany w stopniu wymaganym do utrzymania stałej temperatury (punktu zamarzania lub wrzenia); te napływy energii cieplnej odpowiadają ciepłom fuzji i parowania. Wzrost entropii związany na przykład z topnieniem wynosi ΔHfusion/Tm.
- Pojemność cieplna C danej fazy wyraża ilość ciepła potrzebną do zmiany temperatury o niewielką wartość ΔT , lub dokładniej, o nieskończenie małą wartość dT . Zatem przyrost entropii spowodowany ogrzewaniem substancji w zakresie temperatur, który nie obejmuje przejścia fazowego, jest dany przez sumę wielkości C dT/T dla każdego przyrostu temperatury dT . Jest to oczywiście tylko całka
Ponieważ pojemność cieplna zależy w niewielkim stopniu od temperatury, najdokładniejsze wyznaczanie entropii absolutnych wymaga, aby w powyższej całce zamiast stałej C zastosować zależność funkcyjną C od T.
Gdy nie jest to znane, można wykonać serię pomiarów pojemności cieplnej w wąskich przyrostach temperatury ΔT i zmierzyć pole powierzchni pod każdym odcinkiem krzywej.
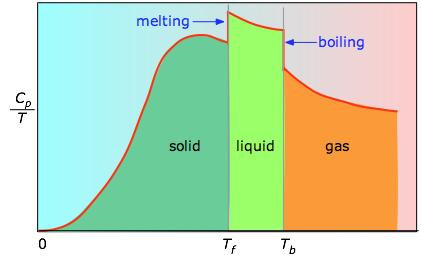
Powierzchnia pod każdym odcinkiem wykresu reprezentuje zmianę entropii związaną z ogrzewaniem substancji w przedziale ΔT. Do tego należy dodać entalpie topnienia, parowania i wszelkich przemian fazowych ciało stałe-ciało stałe. Wartości Cp dla temperatur bliskich zeru nie są mierzone bezpośrednio, ale mogą być oszacowane na podstawie teorii kwantowej.
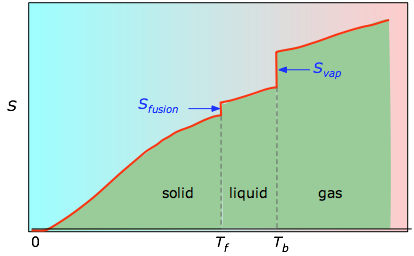
Kumulatywne obszary od 0 K do dowolnej temperatury (wzięte z eksperymentalnego wykresu po lewej stronie) są następnie wykreślane jako funkcja T, a wszelkie entropie przemiany fazowej, takie jak Svap = Hvap / Tb są dodawane, aby uzyskać entropię bezwzględną w temperaturze T.
.