Area of an Irregular Polygon

Ten artykuł opisuje proste rozwiązanie problemu geometrycznego, który znajduję w sieci opisany w zbyt skomplikowany sposób. Problem polega na obliczeniu pola powierzchni i długości obwodu dwuwymiarowej, zamkniętej figury, takiej jak plan piętra pokoju, działka lub jakakolwiek inna dwuwymiarowa figura ograniczona („nieregularny wielokąt”), niezależnie od stopnia złożoności.

Na pewno nie roszczę sobie prawa do oryginalności tej metody. Wersje istniały od czasów Gaussa lub wcześniej. Ale większość artykułów online opisuje tę metodę w niepotrzebnie skomplikowany sposób. Odniesienia obejmują artykuł Wikipedii Shoelace Formula, podobnie złożoną metodę w artykule Polygon, oraz wiele artykułów, które wydają się być obliczone bardziej na zademonstrowanie erudycji autora niż na dostarczenie najmniej złożonego wcielenia metody. Ten artykuł (PDF) pokazuje jedno z najmniej złożonych (ale bynajmniej nie prostych) wyrażeń:

(1) $A = \frac{1}{2} \left| \begin{array}{cc} x_0 & x_1 \ y_0 & y_1 \ end{array} \right| + \left|begin{array}{cc} x_1 & x_2 \ y_1 & y_2 \ \end{array} \right| + \left|begin{array}{cc} x_2 & x_3 \ y_2 & y_3 \ \end{array} \right| + … + \left|begin{array}{cc} x_{n-2} & x_{n-1} \\\ y_{n-2} & y_{n-1} \ end{array} \right| + \left|begin{array}{cc} x_{n-1} & x_0 \ y_{n-1} & y_{n-1} & y_0 \ \ end{array} \gdzie $x_n,y_n$ jest wierzchołkiem wielokąta wyrażonym we współrzędnych kartezjańskich, a $left|begin{array}{cc} x_0 & x_1 \} y_0 & y_1 \} \end{array} \right|$ odnosi się do wyznacznika, o wartości $x_0 \times y_1 – y_0 \times x_1$

Nie zniechęcaj się powyższym opisem – użycie tej metody jest łatwiejsze niż zrozumienie jej matematycznych podstaw. Podczas pracy nad tym artykułem znalazłem wiele odpowiedzi na pytania studentów, które były tak skomplikowane, że nie mogły ich oświecić. W tym artykule zrobię wszystko, co w mojej mocy, aby uczynić tę metodę tak prostą i dostępną, jak to tylko możliwe.

Metoda jest najłatwiejsza do wyrażenia jako algorytm:

• Wierzchołki wielokąta nieregularnego można przedstawić w postaci współrzędnych kartezjańskich: $x,y$.
• Każda para współrzędnych jest przetwarzana w algorytmie sumowania powierzchni, który wygląda następująco:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Prostym wyrażeniem matematycznym dla powyższego byłoby:
  

  (2) Pole wielokąta nieregularnego $
  A = ^frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \czasy y_i – y_{i+1} \times x_i}$

• UWAGA: W równaniu (2), przemierzana liczba kończy się na ostatnim dostarczonym elemencie danych, nie powtarza początkowego elementu, jak pokazano w równaniu (1) powyżej. Dla moich celów, wyjaśnionych poniżej, ta forma jest zamierzona – w badaniu gruntu dane terenowe powinny zamykać figurę, tj. ostatnia pozycja powinna być równa pierwszej. W takim zastosowaniu, automatyczne zamknięcie figury jak w równaniu (1) ukryłoby błędy, które należy ocenić.

  Użytkownicy mogą preferować formę pokazaną w równaniu (1) powyżej, do celów innych niż redukcja danych geodezyjnych. Dla tych celów, podczas przetwarzania po prostu ponownie oceń pierwszą pozycję danych na końcu traversal, lub dostarcz zestawy danych, które powtarzają pierwszą pozycję danych jako ostatnią.

• Tutaj jest kompletna, działająca funkcja Pythona:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Powyższy argument „array” jest zbiorem kartezjańskich współrzędnych $x,y$, tj.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Zauważ w tym zestawie danych, że pierwszy element danych jest powtórzony na końcu.

• Oto nieco bardziej złożona funkcja Pythona, która oblicza zarówno pole powierzchni, jak i długość obwodu:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Znowu to przypomnienie: dla obu powyższych przykładów kodu, w zastosowaniach innych niż redukcja danych geodezyjnych, dostarczony zbiór danych powinien zawierać kopię pierwszego elementu danych jako ostatni, tzn.tj. figura powinna być jawnie zamknięta.

• Wybrałem Pythona dla tych przykładów, ponieważ listing Pythona maksymalizuje znaczenie algorytmów, minimalizując przy tym zbędne elementy.

• Powyższe funkcje można łatwo przekonwertować na inne języki, niemal bezpośrednio – z wyjątkiem pokazanego powyżej sumowania obwodu, które wykorzystuje fakt, że Python obsługuje liczby zespolone. W przypadku języków, które nie obsługują liczb zespolonych, można utworzyć wynik obwodowy w ten sposób:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formalnie, długość obwodu jest sumą magnitud wektorów:
  

  (3) Długość obwodu $displaystyle P = ∑sum_{i=m}^{n-1}{ ∑sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-.y_i)^2}}$

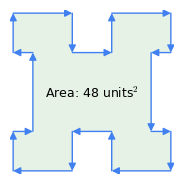
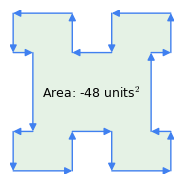Rysunek 1: Wektory zgodne z ruchem wskazówek zegara vs. Wektory przeciwnie do ruchu wskazówek zegara

Oto kilka ważnych własności tej metody:

• Wierzchołek początkowy wybrany w obrębie wielokąta nie ma znaczenia ani dla obliczenia pola powierzchni, ani dla obliczenia obwodu, ważne jest jedynie, aby figura była zamknięta, tzn.tzn. ostatnia współrzędna powinna być równa pierwszej.
• „Reguła ruchu wskazówek zegara”: kolejność wektorów jest istotna – jeśli obwód jest przemierzany zgodnie z ruchem wskazówek zegara, wynik pola powierzchni jest dodatni, jeśli przeciwnie do ruchu wskazówek zegara, jest ujemny (Rysunek 1). To właśnie ta właściwość metody odejmuje pole powierzchni załamań od figury złożonej, jak na rysunku 1 – „załamania” reprezentują trawersowanie w obrębie wielokąta w kierunku przeciwnym do ruchu wskazówek zegara.
• Wiele zastosowań tej metody wykorzystuje oryginalne źródła danych składające się z wektorów biegunowych (przykładem są opisy prawne pomiarów geodezyjnych), ale ta metoda wymaga współrzędnych kartezjańskich. Konwersja ze współrzędnych biegunowych na kartezjańskie jest trywialna, ale należy pamiętać o tym wymaganiu.
• Ponownie, dla dokładnego obliczenia powierzchni, opisany wielokąt powinien być figurą zamkniętą – ostatnia współrzędna powinna być równa pierwszej. W przypadku aplikacji wykorzystujących dane terenowe składające się z wektorów długości, które są następnie przekształcane do postaci kartezjańskiej, warto porównać początkową i końcową współrzędną kartezjańską – powinny być one równe. Na przykład, starsze pomiary geodezyjne (sprzed ery tanich komputerów) regularnie nie zdają tego testu.

Ta sekcja jest w pełni funkcjonalnym komputerem powierzchniowo-perymetrowym, który może przetwarzać wprowadzone pary danych współrzędnych kartezjańskich lub biegunowych, albo geodezyjne opisy prawne. Wystarczy wybrać typ danych (współrzędne kartezjańskie x,y, współrzędne biegunowe m,θ lub geodezyjny opis prawny) i wprowadzić (lub wkleić) dane do poniższego pola wprowadzania danych. Możesz również wybrać przykładowe zestawy danych w celu zapoznania się i przećwiczenia.

Z powodu problemów z bezpieczeństwem przeglądarki, aby uniknąć nadmiernego pisania i importowania znacznych ilości danych z innego źródła, czytelnicy będą musieli użyć schowka systemowego. Wystarczy skopiować dane do schowka w aplikacji źródłowej, a następnie kliknąć obszar wprowadzania danych poniżej i nacisnąć Crtl+A, aby zaznaczyć wszystko, Ctrl+V, aby przesłać dane z innego miejsca, oraz Ctrl+C, aby skopiować własne wprowadzone dane. Większość przeglądarek zawiera funkcje schowka również jako pozycje menu.

Wybierz typ danych:

kartezjański (x,y)

biegunowy (m,θ)

opis badania

Obszar wprowadzania danych: Wybierz wszystko: Ctrl+A | Kopiuj: Ctrl+C | Wklej: Ctrl+V

Obszar wykresów:

Przepraszamy – Twoja przeglądarka nie obsługuje możliwości graficznych, których wymaga ta funkcja –
rozważ zainstalowanie przeglądarki Google Chrome lub Firefox.

Opcje:

Linie

Strzałki

Początek

Środek

Jednostka długości:

Szerokość linii:

Odwrotność

Wyniki:Zaznacz wszystko: Ctrl+A | Kopiuj: Ctrl+C | Wklej: Ctrl+V

Komputer area/perimeter ma trzy tryby wprowadzania danych:

• Pary współrzędnych kartezjańskich (x,y):

  • Każda współrzędna jest dwuwymiarową pozycją z częścią poziomą (x) i pionową (y) (współrzędna kartezjańska).
  • Współrzędne nie kumulują się – każda niezależnie opisuje swoje położenie.
  • Więc kwadrat byłby:
    • 0,0 (początek)
    • 0,100 (góra)
    • 100,100 (prawo)
    • 100,0 (dół)
    • 0,0 (powrót do początku)
  

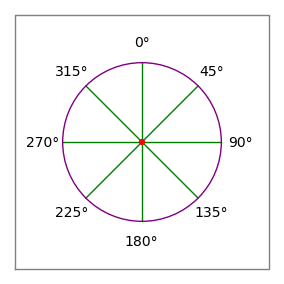  Rysunek 2: Róża kompasowa

  • Przecinki w powyższym przykładzie mają na celu jedynie pogrupowanie par danych dla czytelnika – nie mają one żadnego znaczenia dla parsera danych komputera obszarowego.
  • Parser jest na tyle solidny, że powyższy przykład można wkleić do obszaru wprowadzania danych komputera i będzie on działał (spróbuj).
  • Jedynym ograniczeniem jest to, że komentarze wyjaśniające nie mogą zawierać liczb.

• Pary współrzędnych biegunowych (m,θ):

  • Każda współrzędna składa się z odległości i kąta w stopniach (wektora biegunowego).
  • Kąty są zgodne z konwencją kompasu – 0 stopni to góra lub „północ”, 90 stopni to prawo lub „wschód” (rysunek 2).
  • W przeciwieństwie do wcześniejszej formy kartezjańskiej, współrzędne te są kumulatywne – każdy nowy wektor dodaje się do obecnej pozycji.
  • Więc kwadratem byłby:
    • 100,0 (w górę)
    • 100,90 (w prawo)
    • 100,180 (w dół)
    • 100,270 (z powrotem do początku)
  • Jak poprzednio, ten przykład będzie działał, jeśli zostanie wklejony do obszaru wprowadzania danych w komputerze i wybrany zostanie tryb biegunowy.
  • Uwaga na współrzędne biegunowe, że początek jest domyślny i wstępnie ustawiony na x = 0, y = 0.
  

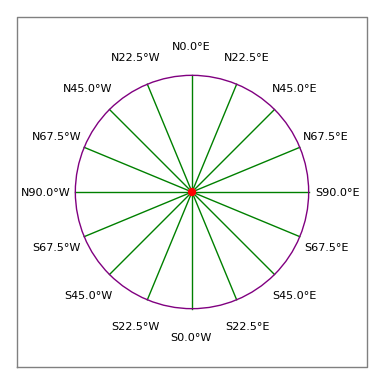  Rysunek 3: Róża kompasowa geodety

• Opis prawny:

  • Po pierwsze, wyjaśnienie związku między wyborem „Jednostki długości” a wyświetlaniem wyników:
    • Dla każdego wielokąta obliczana jest lista wyników powierzchni przy użyciu ustalonego zestawu wspólnych jednostek powierzchni (stopy2, metry2, itd.). Aby ta lista powierzchni była sensowna, muszą być znane wejściowe jednostki długości.
    • W trybie kartezjańskim i biegunowym wpisy danych nie mają jednostek, więc użytkownik wybiera, jakie jednostki przypisać do długości. Kiedy więc użytkownik zmienia jednostki długości, zmieniają się wartości powierzchni, zmieniają się etykiety długości, ale nie zmieniają się wartości długości.
    • W trybie geodezyjnym opis prawny zawiera jednostki długości (stopy, metry itp.), co oznacza, że jednostki długości są predefiniowane przez źródło. Zatem gdy użytkownik zmienia jednostki długości, zmienia to etykiety i wartości długości, a nie wartości powierzchni.
  • Parser opisu geodezyjnego jest zdecydowanie najmniej wiarygodną z trzech metod parsowania danych – jest to bardziej eksperyment niż solidna metoda konwersji danych.
  • Napisałem ten parser pobierając pewną liczbę opisów prawnych (które są podane jako przykłady w powyższym kalkulatorze) i dostrajając kod parsera do momentu, gdy wszystkie mogły być pomyślnie zdekodowane.

  Kryteriami „sukcesu” było to, że wynik będzie miał taką samą powierzchnię kwadratową, jak twierdzi opis, i że figura „zamyka się”.

  • Termin „zamknięcie”, a w szczególności błąd zamknięcia, jest używany w pracach pomiarowych do opisania stopnia, w jakim punkt końcowy trawersu pomiarowego jest równy punktowi początkowemu. W rzeczywistości rzadko jest to prawdą – błędy zamknięcia zwykle wynikają z błędów w pracy w terenie, a starsze pomiary, opublikowane przed pojawieniem się tanich komputerów, zwykle mają raczej słabe zamknięcia, jak również szalenie niedokładne szacunki powierzchni kwadratowej.
  • Geodezyjny opis prawny jest formalnym sposobem opisu działki – jego forma i składnia powstawała przez dziesięciolecia poprzez wzajemnie akceptowane, nieco arbitralne, konwencje podzielane przez geodetów.
  • W przypadku tego komputera obszar/perymetr wprowadzane dane muszą być zgodne z pewnymi ścisłymi konwencjami, których przestrzegają niektóre, ale nie wszystkie, opisy prawne. Zasadniczymi elementami są:
    • Istnienie zwrotu „punkt początku”, który oddziela pewną wstępną treść od tej opisującej wymiary opisywanej działki. Niektóre dokumenty mówią „Prawdziwy punkt początkowy”, niektóre mówią „Prawdziwy punkt początkowy”, a niektóre mówią „Punkt początkowy”. Udany parser musi usunąć treść przed tym zwrotem i zachować wszystko po nim.
    • Seria zwrotów, które opisują specjalny rodzaj wektora biegunowego używanego przez geodetów:
      • Słowo „północ” lub „południe”, lub jego skrót „N” lub „S”.
      • Następnie kąt wyrażony w stopniach, minutach i sekundach.
      • Następnie słowo „wschód” lub „zachód”, lub jego skrót „E” lub „W”.
      • Potem odległość.
      • Potem jednostka odległości – stopy, metry, itp.
  • Tutaj kilka różnych przykładów wektorów geodezyjnych z przykładowych descrtiptions prawnych:
    • N 2°0’0″ W – 63.50 stóp
    • N90°00’00 „W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.86 feet
    • S. 22 degrees 41′ 55″ E. 174.10 feet
  • Notice about the above examples that they all have different syntax. Istnieje wiele istniejących opisów prawnych, których ten parser nie zdekoduje z powodzeniem, tylko dlatego, że nie próbowałem uwzględnić ich składni. Ale ważne jest, aby dodać, że naprawdę solidny parser dla wielu opisów prawnych w istnieniu musiałby być tak inteligentny jak Watson.
  • Użytkownicy tego obszaru/perymetr komputer może chcesz uniknąć składania zwykły tekst opisów prawnych i nadzieję parser będzie zorientować się. Aby dokonać bezpośrednich wpisów ręcznych (lub stworzyć listę trawersów w innym miejscu w celu importu), należy użyć tej konwencji:
    • Pamiętaj, że akceptowalny wpis trawersu składa się ze słowa „Północ” lub „Południe”, lub litery „N” lub „S”, po którym następuje do trzech liczb podających stopnie, minuty i sekundy kąta, po którym następuje słowo „Wschód” lub „Zachód” lub litera „E” lub „W”, po którym następuje odległość, po której następuje jednostka odległości.
    • Więc akceptowalnym zapisem byłoby „N 30 15 45 W 100 stóp”, co oznacza trawers 100 stóp skierowany 30 stopni, 15 minut i 45 sekund na zachód od północy (tj. w przybliżeniu 330 stopni kompasowych, patrz Rysunek 3).
    • Minuty i sekundy wpisy mogą być pominięte, jeśli są równe zero, lub jeśli wpis jest w stopniach dziesiętnych, lub stopniach i minutach dziesiętnych.
  • Nie jest trudno przekonwertować wydrukowany opis prawny do takich wpisów, i istnieje wiele sposobów, aby wykryć błędy. Po wszystkie trawersy zostały wprowadzone, jeśli rysunek nie ma błędu zamknięcia i zgłasza ten sam obszar kwadratowy, jak oryginał, szanse są wpisy są poprawne (lub mają te same błędy, jak oryginalny opis).
  • Po wprowadzeniu opis prawny w ten sposób, jeśli jest niedopuszczalny błąd zamknięcia lub obszar kwadratowy jest błędne, należy pamiętać, że oryginalne dane mogą być błędne. Istnieje dowolna liczba istniejących opisów prawnych, które nigdy nie zostały sprawdzone metodą komputerową, jak ta, i które nigdy nie były poprawne.

Przeglądając przykłady kartezjańskie (x,y), zauważ różne kształty stosunku powierzchni do obwodu. Wielokąt o dziwnym kształcie” ma stosunek pośredni, koło ma najmniejszy stosunek, a przestrzeń Hilberta ma zdecydowanie największy stosunek. Zależność ta rozciąga się na wyższe wymiary, gdzie wiadomo, że kula ma największą objętość na powierzchnię.

W odniesieniu do przykładu z okręgiem – jest to „okrąg jednostkowy”, okrąg o promieniu równym jeden. Dla podanego przykładu, powierzchnia jest zbliżona do $pi$, a obwód do $2pi$, czyli wartości odpowiednie dla koła jednostkowego. Aby te wartości były czymś więcej niż przybliżeniami, aby były dokładnie równe $pi$ i $2pi$, liczba boków wielokąta musiałaby być nieskończona. Zdecydowałem się tego nie robić 🙂

Przykład przestrzeni Hilberta został wygenerowany przy użyciu algorytmu Sage z umiarkowanym wyborem kolejności (aby uniknąć generowania zbyt dużej ilości danych). W zasadzie przestrzeń Hilberta może mieć nieskończony stosunek obwodu do powierzchni w dwóch wymiarach, lub powierzchni do objętości w trzech wymiarach. Aby zobaczyć, jak złożona może być przestrzeń Hilberta, kliknij tutaj, aby zobaczyć przestrzeń Hilberta rzędu 7.

Zauważ w przykładzie Hilberta, że obliczone pole powierzchni jest bliskie 1/2 dla powierzchni 1×1. Idealnie, bez konieczności przekształcania figury liniowej w obszarową i z właściwym algorytmem, pole powierzchni byłoby dokładnie równe 1/2 pola kwadratu o tych samych wymiarach.

Biegunowy tryb wprowadzania danych jest mniej więcej równy grafice żółwiowej, jeśli zastąpić zero stopni przez „w górę”, 90 stopni przez „w prawo”, itd. i jeśli każda sekwencja obrotu i ruchu jest zawarta w jednej komendzie. Użycie trybu wprowadzania biegunowego jest łatwym sposobem na ręczne skonstruowanie złożonego kształtu, ponieważ odległości i kąty są łatwiejsze do śledzenia niż współrzędne kartezjańskie.

Po raz pierwszy użyłem opisanej powyżej metody obliczania powierzchni geodezyjnej wiele lat temu, gdy mieszkałem w wiejskim Oregonie, otoczony ludźmi, którzy potrzebowali znać obszar i obwód swoich nieruchomości. Spotkałem wiele szokujących przykładów, gdzie agenci nieruchomości bezczelnie oszukiwał ludzi, którzy nie mieli sposobu, aby dowiedzieć się, co się dzieje. Na dowolnej liczbie okazji bym obliczyć obszar z opisu prawnego, tylko po to, aby odkryć, że roszczenie aktu gwarancyjnego o powierzchni było dziko niedokładne – i zawsze wyższe niż reality.

Na jednej okazji poproszono mnie, aby podzielić nieruchomość na dwie równe sekcje i stworzyć opisy prawne dla każdego. Ponieważ miałem nowo nabytego Apple II (który miał moc obliczeniową nowoczesnej temperówki), to było bardzo łatwe – ale jak pracowałem zdałem sobie sprawę, że całkowity areał był wyłączony o około trzy akry, około 25% całości. Skonfrontowałem się z firmą tytułową, która bezczelnie odpowiedziała: „Zobacz tutaj, gdzie w akcie notarialnym jest napisane 'mniej więcej’?”

Przy innej okazji rozpocząłem zakup ziemi, ale ostrzeżony przez powyższe doświadczenie, kiedy otrzymałem polisę tytułową postanowiłem wprowadzić jej opis prawny do mojego programu, aby sprawdzić, czy roszczenie o areał było dokładne. Ale ku mojemu przerażeniu odkryłem, że wszystkie polisy tytułowe dla działek w tej sekcji miały ten sam opis prawny – pierwszej badanej nieruchomości. Okazuje się, że firma deweloperska postanowiła zaoszczędzić pieniądze, badając tylko jedną z kilkudziesięciu działek oferowanych na sprzedaż, i włączyć ten opis prawny we wszystkich polisach tytułowych. Byli pewni, że ujdzie im to na sucho – w końcu kto zna się na matematyce?

Po kłótni z firmą tytułową i deweloperem, próbując przekonać ich do zapłacenia za pomiary, aby opisy prawne nie były grzecznymi fikcjami, poddałem się i postanowiłem nie kupować tej ziemi. To było jak dowiadywanie się, jak robi się kiełbasę – można wiedzieć za dużo.

• 04.15.2013 Wersja 1.3. Dodano szczegółowe wyjaśnienie domyślnego formatu danych, tj. list, które powtarzają pierwszy punkt danych jako ostatni.
• 03.24.2013 Wersja 1.2. Dalsza optymalizacja parsera opisu ankiet, dodanie większej ilości pól danych wynikowych.
• 03.23.2013 Wersja 1.1. Poprawiono parser opisu prawnego, aby radził sobie z większą ilością rodzajów opisów, dodano selektor jednostek długości oraz listę wynikową powierzchni w jednostkach wspólnych.
• 03.22.2013 Wersja 1.0. Initial Public Release.