Cálculo ΔS de Ciclos Termodinâmicos
Tambem podemos calcular uma mudança na entropia usando um ciclo termodinâmico. Como você aprendeu anteriormente, a capacidade de calor molar (Cp) é a quantidade de calor necessária para elevar a temperatura de 1 mol de uma substância em 1°C a uma pressão constante. Da mesma forma, Cv é a quantidade de calor necessária para elevar a temperatura de 1 mol de uma substância em 1°C a um volume constante. O aumento da entropia com o aumento da temperatura na Figura \(\PageIndex{2}) é aproximadamente proporcional à capacidade térmica da substância.
Recordar que a variação da entropia (ΔS) está relacionada ao fluxo de calor (qrev) por ΔS = qrev/T. Porque qrev = nCpΔT a pressão constante ou nCvΔT a volume constante, onde n é o número de toupeiras de substância presentes, a mudança de entropia de uma substância cuja temperatura muda de T1 para T2 é a seguinte:
\\
Como você descobrirá em cursos de matemática mais avançados do que é exigido aqui, pode ser mostrado que isto é igual ao seguinte:Para uma revisão dos logaritmos naturais, veja Habilidades Essenciais 6 no Capítulo 11 “Líquidos”.
Similiarmente,
Assim podemos usar uma combinação de medidas de capacidade térmica (Equação 18.20 ou Equação 18.21) e valores medidos experimentalmente de entalpias de fusão ou vaporização se uma mudança de fase estiver envolvida (Equação 18.18) para calcular a mudança de entropia correspondente a uma mudança na temperatura de uma amostra.
Podemos usar um ciclo termodinâmico para calcular a mudança de entropia quando a mudança de fase de uma substância como o enxofre não pode ser medida diretamente. Como observado no exercício no Exemplo 6, enxofre elementar existe em duas formas (parte (a) na Figura \PageIndex (3)): uma forma ortopédica com uma estrutura altamente ordenada (Sα) e uma forma monoclínica menos ordenada (Sβ). A forma ortopédica (α) é mais estável à temperatura ambiente, mas sofre uma transição de fase para a forma monoclínica (β) a temperaturas superiores a 95,3°C (368,5 K). A transição de Sα para Sβ pode ser descrita pelo ciclo termodinâmico mostrado na parte (b) da Figura \PageIndex{3}, na qual o enxofre líquido é um intermediário. A mudança na entropia que acompanha a conversão do enxofre líquido para Sβ (-ΔSfus(β) = ΔS3 no ciclo) não pode ser medida diretamente. Como a entropia é uma função de estado, entretanto, ΔS3 pode ser calculado a partir da mudança de entropia global (ΔSt) para a transição Sα-Sβ, que é igual à soma dos valores ΔS para as etapas do ciclo termodinâmico, usando a Equação 18.20 e parâmetros termodinâmicos tabulados (as capacidades caloríficas de Sα e Sβ, ΔHfus(α), e o ponto de fusão de Sα.)

Solving for ΔS3 dá um valor de -3,24 J/(mol-K). Como esperado para a conversão de um estado menos ordenado (um líquido) para um mais ordenado (um cristal), ΔS3 é negativo.
Como são medidas as entropias
A entropia absoluta de uma substância a qualquer temperatura acima de 0 K deve ser determinada através do cálculo dos incrementos de calor q necessários para trazer a substância de 0 K para a temperatura de interesse, e depois somando as razões q/T. Dois tipos de medições experimentais são necessárias:
- As entalpias associadas a qualquer mudança de fase que a substância possa sofrer dentro da faixa de temperatura de interesse. A fusão de um sólido e a vaporização de um líquido correspondem a aumentos consideráveis no número de microstatos disponíveis para aceitar a energia térmica, de modo que à medida que estes processos ocorrem, a energia fluirá para um sistema, preenchendo estes novos microstatos na medida necessária para manter uma temperatura constante (o ponto de congelamento ou de ebulição); estes fluxos de energia térmica correspondem aos aquecedores de fusão e vaporização. O aumento da entropia associada à fusão, por exemplo, é apenas ΔHfusion/Tm.
- A capacidade térmica C de uma fase expressa a quantidade de calor necessária para alterar a temperatura por uma pequena quantidade ΔT , ou mais precisamente, por uma quantidade infinitesimal dT . Assim, o aumento de entropia provocado pelo aquecimento de uma substância em uma faixa de temperaturas que não abrange uma transição de fase é dado pela soma das quantidades C dT/T para cada incremento de temperatura dT . Esta é, naturalmente, apenas a integral
\
Porque a capacidade térmica é em si ligeiramente dependente da temperatura, as determinações mais precisas das entropias absolutas requerem que a dependência funcional de C sobre T seja usada na integral acima no lugar de um C constante.
Quando isso não é conhecido, pode-se fazer uma série de medições de capacidade térmica sobre incrementos estreitos de temperatura ΔT e medir a área sob cada seção da curva.
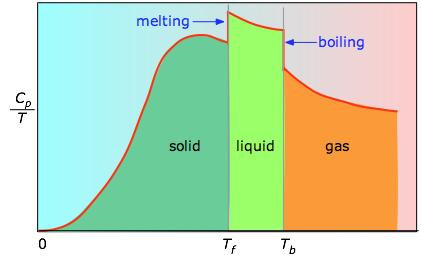
A área sob cada secção da curva representa a alteração de entropia associada ao aquecimento da substância através de um intervalo ΔT. A isto devem ser adicionadas as entalpias de fusão, vaporização e de quaisquer mudanças de fase sólida e sólida. Valores de Cp para temperaturas próximas de zero não são medidos diretamente, mas podem ser estimados a partir da teoria quântica.
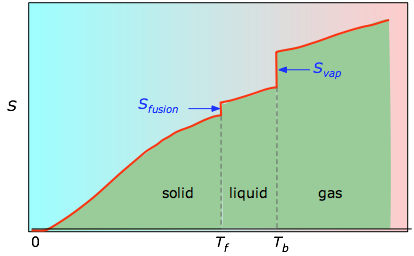
As áreas cumulativas de 0 K a qualquer temperatura (retiradas do gráfico experimental à esquerda) são então plotadas em função de T, e quaisquer entropia de mudança de fase como Svap = Hvap / Tb são adicionadas para obter a entropia absoluta à temperatura T.