No post de hoje, você vai aprender a diferença entre números primos e números compostos. Adicionalmente, mostraremos vários exemplos para ajudá-lo a entendê-los melhor.
Index
O que são números primos?
Números Prime são os números que só são divisíveis por si mesmos e 1, ou seja, se tentarmos dividi-los por outro número, o resultado não é um número inteiro. Então, se você dividir o número por qualquer coisa que não seja um ou por si mesmo, você terá um resto que não é zero.
Números Prime Até 100
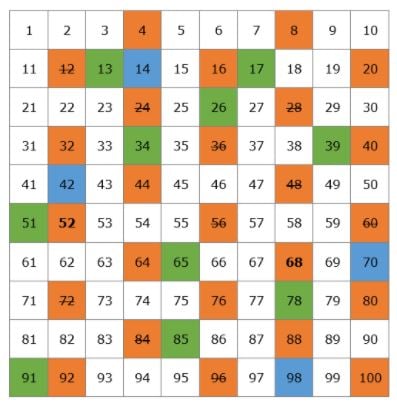
Vamos criar uma tabela com todos os números Prime que existem até 100.
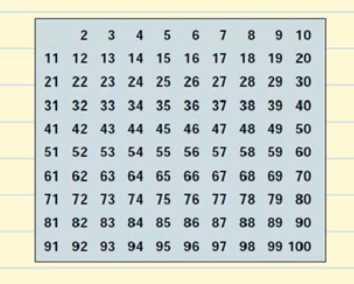
Comecemos com 2. 2 é um número primo mas todos os múltiplos de 2 serão números compostos já que serão divisíveis por 2. Vamos riscar todos os múltiplos de 2 na tabela.
O próximo número primo é 3, assim podemos riscar todos os múltiplos de 3 já que serão números compostos.
Após 3, é o próximo número primo 5, assim podemos riscar todos os múltiplos de 5.
Então temos o número primo 7 e riscamos todos os múltiplos de 7.
O próximo número primo é 11, assim podemos riscar todos os múltiplos de 11 que são 22, 33, 44, 55, 66, 77, 88, e 99. Todos esses números já tinham sido riscados, então terminamos de riscar todos os números compostos da nossa tabela.

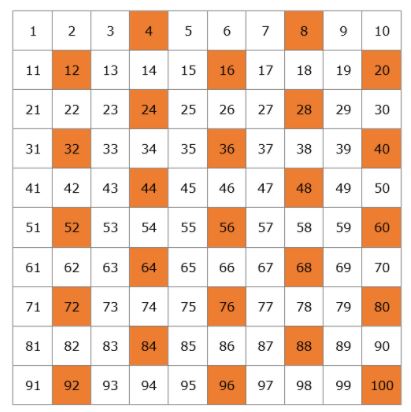
Esta é a nossa lista de números primos de 1 a 100. Você não precisa memorizá-los, mas seria melhor se você se lembrasse dos números menores, como 2, 3, 5, 7, 11, 13.
Quantos Números Prime Existem?
O matemático grego Eratóstenes (século III a.C.) desenhou uma maneira rápida de encontrar todos os números primos até um determinado número. É um processo chamado Sieve of Eratosthenes.
Notem que entre 1 e 100 existem 25 números primos. Quantos números primos existem no total? Nós sabemos desde os tempos antigos que há uma quantidade infinita, então é impossível listar todos eles. Desde Euclides, que foi o primeiro a mostrar que havia uma quantidade infinita no século IV a.C., não conhecia o conceito de infinito, ele disse que “números primos são mais do que qualquer multidão fixa deles” significando que se você imaginar 100, há mais, e se você imaginar um milhão ainda há mais.
Números primos 100 a 1.000
Vamos dar uma olhada nos números primos de 100 a 1.000.

Lamentamos não podermos mostrar todos eles, pois você sabe que há uma quantidade infinita. 😉
Exemplos de números primos
Para ajudar você a entender melhor os números primos, vamos explicar um exercício.
Sara tem 6 peças de doces que ela quer compartilhar, mas ela não sabe com quantas pessoas ela pode compartilhá-los para que todos recebam a mesma quantidade e nenhuma sobra. Quantas maneiras ela pode fazer isso?
Aqui está Sara e seus 6 pedaços de doce:

Como podemos dividi-los?
A primeira e mais fácil maneira é dá-los a uma pessoa, em outras palavras, dividi-los por 1. Desta forma essa pessoa terá 6 pedaços de doce.
A próxima possibilidade é dividi-los entre 2 pessoas. Como 6 dividido por 2 é 3, cada pessoa receberá 3 pedaços de doce!

Vamos continuar com o próximo número, 3. Se dividirmos 6 pedaços de doce entre 3 pessoas é também uma divisão exata e cada pessoa receberá 2 pedaços de doce:

Vamos continuar com os números. Não temos divisões exatas com 4 e 5, mas fazemos com 6.
Desde que 6 dividido por 6 é 1, podemos dar a 6 crianças 1 pedaço de doce cada uma.

Vamos recolher algumas informações. Temos 6 pedaços de doce que podemos compartilhar (com uma divisão exata) entre 1, 2, 3, e 6 pessoas. Em outras palavras, podemos dividir o número 6 e obter 0 como o restante quando o dividimos por 1, 2, 3, e 6. Estes números são conhecidos como os divisores de 6.
Vamos tentar com outro número, 7 por exemplo.
Agora a Sara tem 7 pedaços de doce e quer partilhá-los, mas não sabe com quantas pessoas pode partilhá-los para que todos recebam a mesma quantidade e nenhuma fique sobrando. Quantas maneiras ela pode fazer isso?

Henry é tão sortudo! Ele tem todos os pedaços de doces!
Existem outras formas de o fazer? Não podemos dividir 7 por 2, 3, 4, 5, ou 6, …mas 7 é possível!
Sara pode dividir os pedaços de doce entre 7 pessoas, dando-lhes um pedaço cada:

Então 7 só pode ser dividido por 1 e 7, os seus únicos divisores são 1 e 7. Estes são os tipos de números que chamamos de números primos.
Existem mais números primos? Claro que sim! Vamos procurar mais:
- É 4? Não! Porque os seus divisores são 1, 2, e 4.
- É 5? Sim! Porque os seus divisores são 1 e 5.
- É 8? Não! Porque os seus divisores são 1, 2, 4, e 8.
Em suma, um número é primo se tiver apenas 2 divisores: 1 e ele próprio.
Agora você pode procurar muitos números primos!
Como encontrar números primos
Ponha muita atenção! Vamos dar-lhe um truque para saber se um número é prime ou não, sem ter de procurar os seus divisores, mas de uma forma mais divertida e dá-nos os divisores (se os tiverem).
Vamos escolher um número ao acaso, 16 por exemplo.
Para verificar se é ou não um número prime, vamos usar uma tabela muito semelhante às cartas Montessori para multiplicar. E vamos obter tantas bolas quanto o número que escolhemos. Neste caso, 16 bolas.
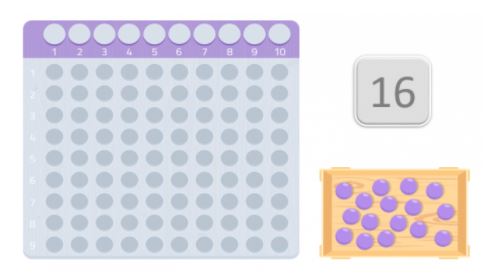
Após termos a mesa e as bolas, devemos colocá-las na mesa começando com o primeiro espaço, tentando formar um retângulo. Os números que compõem as bordas do retângulo são os divisores desse número.
No caso de só conseguirmos formar um retângulo com o mesmo número que estamos usando e o número 1, será um número primo.
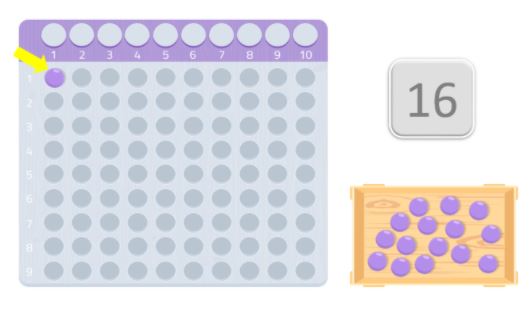
Por exemplo, neste caso, colocamos 8 bolas na primeira linha e mais 8 na segunda. Como você pode ver, nós formamos um retângulo e podemos ver que 8, como 2, são divisores do número 16. Portanto, 16 não é um número primo porque, como você sabe, números primos são aqueles que são apenas divisíveis por si mesmos e 1,
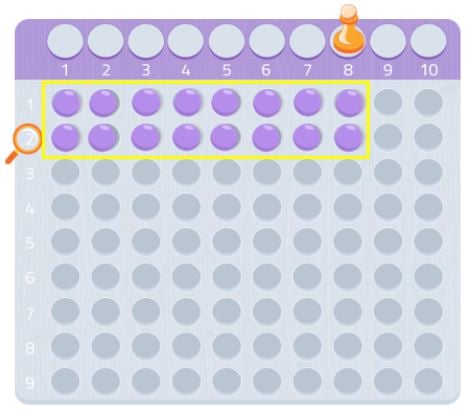
Podemos tentar com outro número, 7 por exemplo.
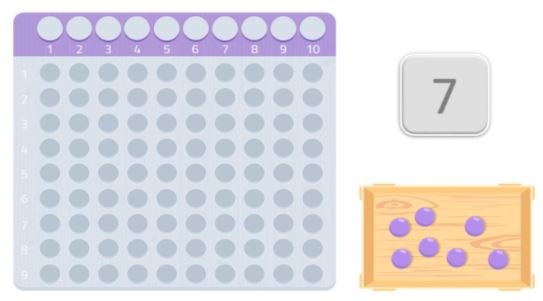
Como podemos ver, não podíamos fazer um rectângulo completo, faltar-nos-ia uma bola. Como não conseguimos formar um rectângulo, poderíamos dizer que o número 7 não tem outros divisores a não ser ele próprio e 1, como podemos ver na imagem seguinte.
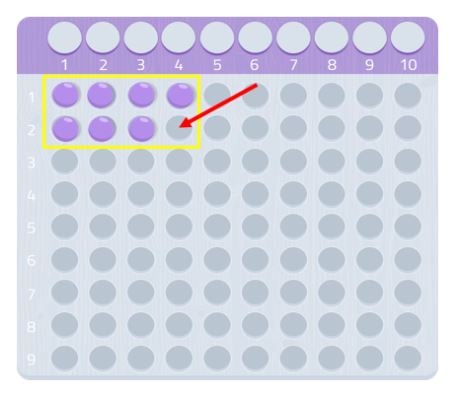
Por isso, 7 é um número primo!
Tente qualquer outro número, verá como funciona! Você pode usar papel gráfico e procurar por retângulos usando esse número de quadrados.
Por que os números primos são importantes?
Números primos são a chave para a aritmética, abaixo você verá um exemplo que demonstra sua importância, não só em matemática mas também na natureza.
O que queremos dizer quando dizemos que números primos são a chave para a aritmética?
Isto porque qualquer número consiste num produto único composto por uma série destes números.
Acredita-se que tenham sido estudados durante cerca de 20.000 anos quando um antepassado nosso escreveu uma série de números primos (11, 13, 17, e 19) no osso Ishango. Como se isso fosse uma coincidência, foi confirmado que os antigos egípcios estavam trabalhando com eles há 4.000 anos.
Além disso, a natureza os conhece muito bem e algumas espécies foram capazes de descobri-los ao longo de sua evolução e aproveitá-los para sobreviver.
Refiro-me a várias espécies de cigarras, como a Magicicada septendecium que vive na América do Norte. Esta espécie da cigarra estabeleceu seu ciclo de reprodução em torno de 13 ou 17 anos, não 12, 14, 15, 16, ou 18 – exatamente 13 ou 17. Isto permite-lhes evitar predadores que também têm ciclos reprodutivos periódicos; imagine um predador com um ciclo reprodutivo de 4 anos.
Se o ciclo de vida de uma cigarra fosse de 12 ou 14 anos, coincidiria com um predador muito frequentemente, muito mais do que se fosse de 13 ou 17 anos. Exatamente 2 vezes a cada 100 anos, enquanto que, caso contrário, elas coincidiriam em 11 ciclos que comprometeriam o desenvolvimento da espécie.
>
>
A segurança da comunicação eletrônica é baseada em números primos também. Toda mensagem criptografada enviada pela internet (redes de mensagens, compras ou banco eletrônico) tem um grande número associado a ela, e é muito difícil saber onde ela está prime ou não. O receptor tem um de seus divisores, e é por isso que eles podem descriptografá-lo. Portanto, ter números primos é fundamental para a nossa privacidade quando comunicamos electronicamente.
What Are Composite Numbers?
Números compostos são aqueles números que são divisíveis por 1 e eles mesmos, bem como outros números.
Vamos olhar para um exemplo de um número prime e um número composto.
11 pode ser escrito como a multiplicação 1 x 11, mas não pode ser escrito como qualquer outra multiplicação de números naturais. Ele só tem os divisores 1 e 11, e portanto é um número primo.
12 pode ser escrito como a multiplicação 1 x 12 e como a multiplicação 3 x 4, e 2 x 6. Como 12 é divisível por mais números que 1 e por si só, 12 é um número composto.
Is 1 a Prime Number?
Existem pessoas que acreditam nisso porque dizem que 1 só pode ser dividido por 1 e por si mesmo, mas em matemática, o número 1 foi descartado como um número primo porque só tem um divisor. Na verdade, o critério de “um inteiro positivo é prime se ele tiver exatamente dois divisores positivos” é usado para excluir o número um da lista de números primos. Não é porque estamos sendo picuinhas sobre isso, mas se o número um fosse considerado prime então muitas propriedades matemáticas teriam que ser ditas de forma diferente.
Então, 1 é um Número Composto?
Bem, ele também não é composto já que não pode ser colocado como produto de números primos. O número 1 não é um número primo ou composto. E antes de perguntar, zero também não é prime ou composto, mas isto porque todas as considerações que estávamos a explicar para números positivos, ou seja, maiores que zero.
Divisores de um Número
O divisor de um número é o valor que divide o número em partes exactas, por outras palavras, tem um resto de 0.
Como exemplo, vamos calcular os divisores para 24,
Começamos a dividir com os menores números começando por 1,
- 24 / 1 = 24. Ambos 1 e 24 são divisores.
- 24 / 2 = 12. Então 2 e 12 são divisores.
- 24 / 3 = 8. Então 3 e 8 são divisores.
- 24 / 4 = 6. Então 4 e 6 são divisores.
- 24 / 5 = 4. Não é uma divisão exata e tem um resto de 4, então 5 não é um divisor.
O próximo número é 6, mas como já sabemos que 6 é um divisor de 24 acabamos de calcular os divisores para 24.
Vídeo: Factorização e números primos
Se quiser saber mais sobre números primos e números compostos, veja o vídeo a seguir. Você também aprenderá o conceito de factoring usando a tabela Montessori.
Este vídeo é um dos nossos tutoriais interativos e, embora não seja interativo, você ainda pode assisti-lo quantas vezes precisar e compartilhá-lo com os amigos. Se você gostaria de acessar nossos tutoriais interativos, registre-se com Smartick! O método online para ajudar crianças de 4 a 14 anos a aprender e praticar matemática.
Se você gostaria de continuar aprendendo sobre números primos e a melhor matemática adaptada ao seu nível, registre-se com Smartick e experimente grátis!
Aprenda Mais:
- Números Primários e Números Compostos
- Números Primários: Um truque para ajudá-lo a identificá-los
- Números Primeiros: Como encontrá-los com a peneira de Eratóstenes
- Aprenda a considerá-los em Prime Numbers
- Prime Numbers Activities with Smartick



- Autor
- Posições recentes
Uma equipa multidisciplinar e multicultural composta por matemáticos, professores, professores e outros profissionais da educação!
Propõe a criação do melhor conteúdo matemático possível.
- Exemplos de Problemas de Palavras Matemáticas do 3º Grau com Soluções – 25/03/2021
- Ângulos Interiores Consecutivos: O que são e como encontrá-los com exemplos – 11/03/2021
- Exemplos de problemas de palavras de segunda classe com soluções – 04/02/2021