Você encontra fatores em todos os combinatórios porque foi de lá que eles se originaram. O factorial foi criado como uma forma de expressar o número de arranjos de um grupo de itens, o qual, claro, encontramos usando, na sua forma mais básica, a regra de multiplicação da contagem.
O factorial é uma espécie de operação não oficial da regra de multiplicação da contagem.
Porquê o Factorial Zero é igual a 1
É aqui que se torna complicado, porque se pensarmos apenas nos factores no contexto dos quais eles são normalmente definidos, i.e. o “produto de todos os inteiros positivos menor ou igual ao número” então descobrir 0! é como bater numa parede de tijolos.
A maioria das pessoas dirá que 0! é definido como 1, e se você perguntar porque eles apenas dizem “porque é definido como um”.
Sim, é bastante frustrante. É o equivalente matemático a perguntar aos teus pais porque é que tens de seguir alguma regra arbitrária que eles inventaram e ser informado, “porque eu disse”.
Embora isso possa ser uma técnica parental aceite, é uma péssima maneira de aprender matemática. Então, qual é o acordo? Como decidimos que zero factorial é igual a um?
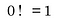
Um entendimento intuitivo
Lembrar como dissemos que o factorial teve origem na operação matemática de encontrar o número de permutações ou arranjos de um conjunto? (Nota: não as permutações de um conjunto menor de um conjunto maior, mas apenas os arranjos de um determinado conjunto.)
Zero factorial pode ser pensado como o número de arranjos de elementos zero num conjunto, também conhecido como conjunto vazio {}. (Se você já estudou conjuntos, talvez em estatística básica ou matemática discreta, você provavelmente está familiarizado com o conceito de conjunto vazio. É literalmente o conjunto de nada.)
Agora se eu lhe perguntasse quantos arranjos há de uma coisa você responderia 1 porque só há uma maneira de arranjar uma coisa. A mesma ideia segue aqui. Nossa “uma coisa” é o conjunto vazio, e o número de arranjos do conjunto vazio é um. É isso mesmo. É por isso que 0! é igual a 1.
Como simplificar as expressões fatoriais
Agora que temos o básico, está na hora do coração do nosso tutorial fatorial: simplificar.
A melhor maneira de ver a matemática está em ação. Então, aqui estou eu para te acompanhar através dos seis problemas mostrados na imagem no topo deste post! Vamos começar bem e fácil, depois passar para a fórmula de combinações com números e depois variáveis, e terminar com algumas expressões factoriais mais complicadas.
❤ STAY CONNECTED ❤
Não perca uma batida, ou um problema matemático!