Um fluido de trabalho contém energia potencial (cabeça de pressão) e energia cinética (cabeça de velocidade). O fluido pode ser compressivo ou incompressível. Vários princípios físicos são empregados pelas turbinas para coletar essa energia:
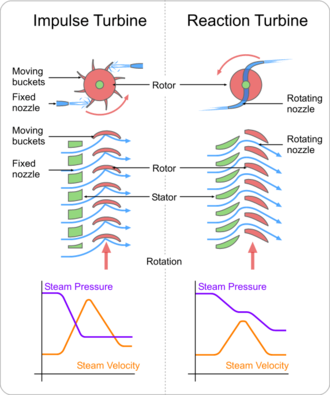
Turbinas de impulso mudam a direção do fluxo de um fluido de alta velocidade ou jato de gás. O impulso resultante gira a turbina e deixa o fluxo do fluido com energia cinética diminuída. Não há mudança de pressão do fluido ou gás nas pás da turbina (as pás móveis), como no caso de uma turbina a vapor ou a gás, toda a queda de pressão ocorre nas pás estacionárias (os bicos). Antes de chegar à turbina, a cabeça de pressão do fluido é alterada para cabeça de velocidade acelerando o fluido com um bico. As rodas Pelton e as turbinas de Laval utilizam este processo exclusivamente. As turbinas de impulso não requerem uma caixa de pressão ao redor do rotor, uma vez que o jacto do fluido é criado pelo bico antes de atingir as pás no rotor. A segunda lei de Newton descreve a transferência de energia para as turbinas de impulso. As turbinas de impulso são mais eficientes para uso em casos em que o fluxo é baixo e a pressão de entrada é alta.
Turbinas de reação desenvolvem torque reagindo à pressão ou massa do gás ou do fluido. A pressão do gás ou do fluido muda conforme ele passa pelas pás do rotor da turbina. Uma caixa de pressão é necessária para conter o fluido de trabalho, uma vez que ele age no(s) estágio(s) da turbina ou a turbina deve estar totalmente imersa no fluxo do fluido (como nas turbinas eólicas). A carcaça contém e direciona o fluido de trabalho e, para turbinas de água, mantém a sucção transmitida pelo tubo de sucção. As turbinas Francis e a maioria das turbinas de vapor utilizam este conceito. Para fluidos de trabalho compressíveis, os vários estágios da turbina são normalmente usados para aproveitar o gás em expansão de forma eficiente. A terceira lei de Newton descreve a transferência de energia para as turbinas de reação. As turbinas de reação são mais adequadas para velocidades de fluxo mais altas ou aplicações onde a cabeça do fluido (pressão a montante) é baixa.
No caso de turbinas a vapor, como as que seriam usadas para aplicações marítimas ou para a geração de eletricidade em terra, uma turbina de reação do tipo Parson exigiria aproximadamente o dobro do número de linhas de pás como uma turbina de impulso do tipo de Laval, para o mesmo grau de conversão de energia térmica. Embora isto torne a turbina Parsons muito mais longa e pesada, a eficiência global de uma turbina de reacção é ligeiramente superior à da turbina de impulso equivalente para a mesma conversão de energia térmica.
Na prática, os projectos modernos de turbinas utilizam tanto conceitos de reacção como de impulso em diferentes graus sempre que possível. As turbinas eólicas usam um aerofólio para gerar um elevador de reação a partir do fluido em movimento e transmiti-lo ao rotor. As turbinas eólicas também ganham alguma energia do impulso do vento, ao desviá-lo em um ângulo. Turbinas com múltiplos estágios podem usar a reação ou o pisco de impulso a alta pressão. As turbinas a vapor eram tradicionalmente mais impulsivas, mas continuam a se mover em direção a projetos de reação similares aos utilizados em turbinas a gás. A baixa pressão o fluido de operação se expande em volume para pequenas reduções na pressão. Sob estas condições, o blading torna-se estritamente um projeto do tipo reação com a base da pá unicamente de impulso. O motivo é devido ao efeito da velocidade de rotação para cada pá. À medida que o volume aumenta, a altura da pá aumenta, e a base da pá gira a uma velocidade mais lenta em relação à ponta. Esta mudança na velocidade força um projetista a mudar de impulso na base, para uma ponta de alto estilo de reação.
Métodos clássicos de projeto de turbinas foram desenvolvidos em meados do século XIX. A análise vectorial relacionou o fluxo de fluido com a forma e rotação da turbina. Métodos gráficos de cálculo foram usados no início. As fórmulas para as dimensões básicas das peças da turbina estão bem documentadas e uma máquina altamente eficiente pode ser projetada de forma confiável para qualquer condição de fluxo de fluido. Alguns dos cálculos são fórmulas empíricas ou “regra de ouro”, e outros são baseados na mecânica clássica. Como na maioria dos cálculos de engenharia, foram feitas suposições simplificadas.

Triângulos de velocidade podem ser usados para calcular o desempenho básico de um estágio de turbina. O gás sai das palhetas guia de bicos estacionários da turbina à velocidade absoluta Va1. O rotor gira à velocidade U. Em relação ao rotor, a velocidade do gás à medida que este colide com a entrada do rotor é Vr1. O gás é girado pelo rotor e sai, em relação ao rotor, à velocidade Vr2. No entanto, em termos absolutos, a velocidade de saída do rotor é Va2. Os triângulos de velocidade são construídos utilizando estes vários vectores de velocidade. Os triângulos de velocidade podem ser construídos em qualquer secção através do rotor (por exemplo: cubo, ponta, secção média e assim por diante) mas normalmente são mostrados no raio médio do estágio. O desempenho médio do estágio pode ser calculado a partir dos triângulos de velocidade, neste raio, usando a equação de Euler:
Δ h = u ⋅ Δ v w {\displaystyle \Delta h=u\cdot \Delta v_{w}}}

Hence:
Δ h T = u ⋅ v w T {\i1}displaystyle {\i}{\i}={\i1}frac {\i}{\i}delta h}={\i}delta v_{\i}{\i}{\i}

where:
Δ h {\i1}displaystyle {\i}delta h

é a queda específica de entalpia através do palco T {\i1}displaystyle T

é a variação da velocidade de turbilhão
A relação de pressão da turbina é uma função de Δ h T {\i1}displaystyle {\i}{\i1}delta h}{\i}

e a eficiência da turbina.
O desenho moderno da turbina leva os cálculos mais longe. A dinâmica dos fluidos computacional dispensa muitas das suposições simplificadoras usadas para derivar fórmulas clássicas e software de computador facilita a otimização. Estas ferramentas levaram a melhorias constantes no projeto da turbina nos últimos quarenta anos.
A classificação numérica primária de uma turbina é a sua velocidade específica. Este número descreve a velocidade da turbina em sua máxima eficiência em relação à potência e vazão. A velocidade específica é derivada para ser independente do tamanho da turbina. Dadas as condições de fluxo do fluido e a velocidade de saída do eixo desejado, a velocidade específica pode ser calculada e um projeto apropriado da turbina pode ser selecionado.
A velocidade específica, juntamente com algumas fórmulas fundamentais podem ser usadas para dimensionar de forma confiável um projeto existente de desempenho conhecido para um novo tamanho com desempenho correspondente.
O desempenho do projeto da turbina é normalmente exibido como um mapa da turbina ou característica.
O número de pás no rotor e o número de palhetas no estator são frequentemente dois números primos diferentes, a fim de reduzir os harmônicos e maximizar a freqüência de passagem das pás.