Calcularea ΔS din cicluri termodinamice
Potem calcula, de asemenea, o variație a entropiei folosind un ciclu termodinamic. După cum ați învățat anterior, capacitatea termică molară (Cp) este cantitatea de căldură necesară pentru a crește temperatura unui mol dintr-o substanță cu 1°C la presiune constantă. În mod similar, Cv este cantitatea de căldură necesară pentru a crește temperatura unui mol dintr-o substanță cu 1°C la volum constant. Creșterea entropiei odată cu creșterea temperaturii din figura \(\PageIndex{2}\) este aproximativ proporțională cu capacitatea termică a substanței.
Reamintim că modificarea entropiei (ΔS) este legată de fluxul de căldură (qrev) prin ΔS = qrev/T. Deoarece qrev = nCpΔT la presiune constantă sau nCvΔT la volum constant, unde n este numărul de moli de substanță prezentă, variația entropiei pentru o substanță a cărei temperatură se schimbă de la T1 la T2 este următoarea:
\
După cum veți descoperi la cursuri de matematică mai avansate decât cele cerute aici, se poate demonstra că acest lucru este egal cu următoarele:Pentru o trecere în revistă a logaritmilor naturali, consultați Competențele esențiale 6 din Capitolul 11 „Lichide”.
\
În mod similar,
\
Acum putem folosi o combinație de măsurători ale capacității termice (Ecuația 18.20 sau Ecuația 18.21) și valori măsurate experimental ale entalpiei de fuziune sau de vaporizare dacă este implicată o schimbare de fază (Ecuația 18.21).18) pentru a calcula modificarea entropiei corespunzătoare unei modificări a temperaturii unei probe.
Potem folosi un ciclu termodinamic pentru a calcula modificarea entropiei atunci când modificarea de fază pentru o substanță precum sulful nu poate fi măsurată direct. După cum s-a observat în exercițiul din exemplul 6, sulful elementar există în două forme (partea (a) din figura \(\PageIndex{3}\)): o formă ortorombică cu o structură foarte ordonată (Sα) și o formă monoclinică mai puțin ordonată (Sβ). Forma ortorombică (α) este mai stabilă la temperatura camerei, dar suferă o tranziție de fază la forma monoclinică (β) la temperaturi mai mari de 95,3°C (368,5 K). Tranziția de la Sα la Sβ poate fi descrisă prin ciclul termodinamic prezentat în partea (b) din figura \(\PageIndex{3}\), în care sulful lichid este un intermediar. Modificarea entropiei care însoțește conversia sulfului lichid în Sβ (-ΔSfus(β) = ΔS3 în ciclu) nu poate fi măsurată direct. Cu toate acestea, deoarece entropia este o funcție de stare, ΔS3 poate fi calculată din variația entropiei globale (ΔSt) pentru tranziția Sα-Sβ, care este egală cu suma valorilor ΔS pentru etapele din ciclul termodinamic, folosind ecuația 18.20 și parametrii termodinamici tabelari (capacitățile termice ale lui Sα și Sβ, ΔHfus(α), și punctul de topire al lui Sα.)

Soluția pentru ΔS3 dă o valoare de -3,24 J/(mol-K). Așa cum era de așteptat pentru transformarea unei stări mai puțin ordonate (un lichid) într-una mai ordonată (un cristal), ΔS3 este negativă.
Cum se măsoară entropia
Entropia absolută a unei substanțe la orice temperatură peste 0 K trebuie determinată prin calcularea creșterilor de căldură q necesare pentru a aduce substanța de la 0 K la temperatura de interes și apoi prin însumarea rapoartelor q/T. Sunt necesare două tipuri de măsurători experimentale:
- Entalpiile asociate cu orice schimbări de fază pe care le poate suferi substanța în intervalul de temperatură de interes. Topirea unui solid și vaporizarea unui lichid corespund unor creșteri considerabile ale numărului de microstații disponibile pentru a accepta energie termică, astfel încât, pe măsură ce aceste procese au loc, energia va intra într-un sistem, umplând aceste noi microstații în măsura necesară pentru a menține o temperatură constantă (punctul de congelare sau de fierbere); aceste intrări de energie termică corespund căldurilor de fuziune și de vaporizare. Creșterea entropiei asociată cu topirea, de exemplu, este doar ΔHfuziune/Tm.
- Capacitatea termică C a unei faze exprimă cantitatea de căldură necesară pentru a modifica temperatura cu o cantitate mică ΔT , sau, mai precis, cu o cantitate infinitezimală dT . Astfel, creșterea entropiei provocată de încălzirea unei substanțe într-un interval de temperaturi care nu cuprinde o tranziție de fază este dată de suma cantităților C dT/T pentru fiecare creștere a temperaturii dT . Aceasta este, bineînțeles, doar integrala
\
Pentru că capacitatea termică este ea însăși ușor dependentă de temperatură, cele mai precise determinări ale entropiilor absolute necesită ca în integrala de mai sus să se utilizeze dependența funcțională a lui C de T în locul unei constante C.
\
Când acest lucru nu este cunoscut, se poate face o serie de măsurători ale capacității termice pe intervale înguste de temperatură ΔT și se poate măsura aria de sub fiecare secțiune a curbei.
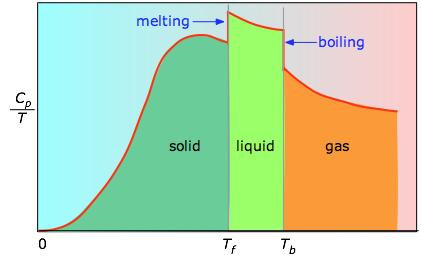
Aria de sub fiecare secțiune a graficului reprezintă modificarea entropiei asociată cu încălzirea substanței printr-un interval ΔT. La aceasta se adaugă entalpiile de topire, vaporizare și a oricăror schimbări de fază solid-solid. Valorile lui Cp pentru temperaturi apropiate de zero nu sunt măsurate direct, dar pot fi estimate din teoria cuantică.
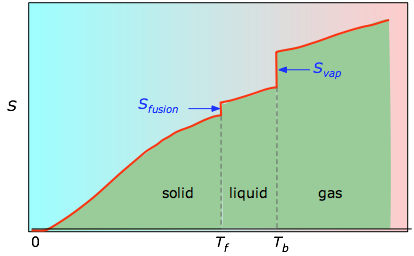
Suprafețele cumulate de la 0 K până la orice temperatură dată (luate din graficul experimental din stânga) sunt apoi reprezentate grafic în funcție de T, iar orice entropii de schimbare de fază, cum ar fi Svap = Hvap / Tb, sunt adăugate pentru a obține entropia absolută la temperatura T.
.