Ecuația logistică (numită uneori modelul Verhulst sau curba de creștere logistică) este un model de creștere a populației publicat pentru prima dată de Pierre Verhulst (1845, 1847). Modelul este continuu în timp, dar o modificare a ecuației continue într-o ecuație discretă de recurență pătratică cunoscută sub numele de harta logistică este, de asemenea, utilizată pe scară largă.
Versiunea continuă a modelului logistic este descrisă de ecuația diferențială
 |
(1)
|
unde 
este parametrul malthusian (rata de creștere maximă a populației) și 
este așa-numita capacitate de încărcare (i.e., populația maximă sustenabilă). Împărțind ambele părți cu 
și definind 
se obține atunci ecuația diferențială
 |
(2)
|
care este cunoscută sub numele de ecuația logistică și are soluția
 |
(3)
|
Funcția 
este cunoscută uneori sub numele de funcția sigmoidă.
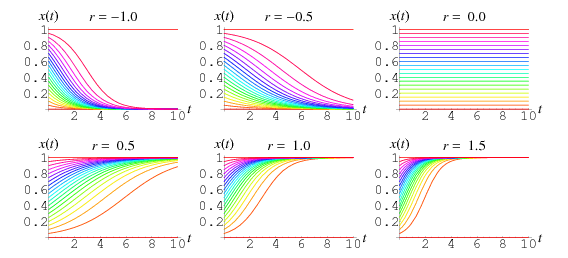
În timp ce 
este de obicei constrânsă să fie pozitivă, sunt prezentate diagrame ale soluției de mai sus pentru diferite valori pozitive și negative ale lui 
și condiții inițiale 
cuprinse între 0,00 și 1,00 în pași de 0,05.
Versiunea discretă a ecuației logistice (3) este cunoscută sub numele de harta logistică.
Curba
 |
(4)
|
obținută din (3) este uneori cunoscută sub numele de curba logistică. În mod similar, o formă normalizată a ecuației (3) este utilizată în mod obișnuit ca o distribuție statistică cunoscută sub numele de distribuție logistică.
.