Găsești factoriale peste tot în combinatorică, pentru că acolo își au originea. Factorialul a fost creat ca o modalitate de a exprima numărul de aranjamente ale unui grup de elemente, pe care, bineînțeles, îl găsim folosind, în forma sa cea mai elementară, regula înmulțirii de numărare.
Factorialul este un fel de operație neoficială a regulii înmulțirii de numărare.
De ce zero factorial este egal cu 1
Aici devine complicat pentru că dacă ne gândim la factoriali doar în contextul în care sunt definiți de obicei, adică.adică „produsul tuturor numerelor întregi pozitive mai mici sau egale cu numărul”, atunci să ne dăm seama de 0! este ca și cum ne-am lovi de un zid de cărămidă.
Majoritatea oamenilor vă vor spune că 0! este definit ca 1, iar dacă îi întrebați de ce vă vor spune doar „pentru că este definit ca 1”.
Da, este destul de frustrant. Este echivalentul matematic al întrebării părinților tăi de ce trebuie să urmezi o regulă arbitrară pe care au inventat-o ei și să ți se spună: „pentru că așa am spus eu.”
Deși asta ar putea fi o tehnică parentală acceptată, este o modalitate proastă de a învăța matematica. Așadar, care este treaba? Cum am decis că zero factorial este egal cu unu?
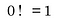
O înțelegere intuitivă
Îți amintești cum am spus că factorialul își are originea în operația matematică de găsire a numărului de permutări sau aranjamente ale unui set? (Notă: nu permutările unui set mai mic dintr-un set mai mare, ci doar aranjamentele unui set dat.)
Factoriala zero poate fi gândită ca fiind numărul de aranjamente ale elementelor zero dintr-un set, aka setul gol {}. (Dacă ați studiat vreodată seturi, poate în cadrul statisticilor de bază sau al matematicii discrete, probabil că sunteți familiarizați cu conceptul de set gol. Este literalmente setul de nimic.)
Acum, dacă v-aș întreba câte aranjamente există pentru un lucru, ați răspunde 1, deoarece există un singur mod de a aranja un lucru. Aceeași idee rezultă și aici. „Un singur lucru” al nostru este setul gol, iar numărul de aranjamente ale setului gol este unu. Asta este tot. Iată de ce 0! este egal cu 1.
Cum să simplificăm expresiile factoriale
Acum că avem elementele de bază în spate, este timpul pentru inima tutorialului nostru factorial: simplificarea.
Cel mai bun mod de a vedea matematica este în acțiune. Așa că iată-mă aici pentru a vă conduce prin cele șase probleme prezentate în imaginea din partea de sus a acestei postări! Vom începe frumos și ușor, apoi vom trece la formula de combinații cu numere și apoi cu variabile și vom încheia cu câteva expresii factoriale mai dificile.
❤ STAY CONNECTED ❤
Nu pierdeți nici un ritm, nici o problemă de matematică!