Área de un polígono irregular

Este artículo describe una solución sencilla a un problema geométrico, uno que encuentro descrito de forma excesivamente compleja en internet. El problema consiste en calcular el área y la longitud del perímetro de una figura bidimensional cerrada, como el plano de una habitación, o un terreno, o cualquier otra figura bidimensional delimitada (un «polígono irregular»), independientemente de su complejidad.

Desde luego, no pretendo que este método sea original. Han existido versiones desde la época de Gauss o antes. Pero la mayoría de los artículos en línea describen el método de forma innecesariamente compleja. Las referencias incluyen el artículo de Wikipedia Shoelace Formula, un método similarmente complejo en el artículo Polygon, y un número de artículos que parecen calculados más para demostrar la erudición del autor que para proporcionar la encarnación menos compleja del método. Este artículo (PDF) muestra una de las expresiones menos complejas (pero de ninguna manera simple):

(1) $A = \frac{1}{2} \left\{\left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\\\\nd{array} \derecha + izquierda x_1 & x_2 y_1 & y_2 \ ~ – fin de la matriz + izquierda: x_2 & x_3 y_2 & y_3. \…derecha… + …izquierda… + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \ y_{n-2} & y_{n-1}{end{array}{c} + izquierda – empezar – matriz – x_{n-1} & x_0 – y_{n-1} & y_0 – terminar – matriz \Donde $x_n,y_n$ es un vértice del polígono expresado en coordenadas cartesianas, y $\left|\begin{array}{cc} x_0 & x_1 \\ y_0 & y_1\\\\\nd{array} \right|$ se refiere a un determinante, con el valor $x_0 \times y_1 – y_0 \times x_1$

No se desanime por la exposición anterior – el uso de este método es más fácil que la comprensión de sus fundamentos matemáticos. Mientras investigaba este artículo, encontré un gran número de respuestas a preguntas de estudiantes que eran tan complejas que no podían iluminar al estudiante. En este artículo voy a hacer todo lo posible para que este método sea lo más sencillo y accesible posible.

El método se expresa más fácilmente como un algoritmo:

• Los vértices de un polígono irregular pueden representarse como coordenadas cartesianas: $x,y$.
• Cada par de coordenadas se procesa en un algoritmo de suma de áreas que tiene el siguiente aspecto:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Una expresión matemática sencilla para lo anterior sería:
  

  (2) Área del polígono irregular $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \N – y_{i+1} \times x_i}$

• NOTA: En la ecuación (2), la figura recorrida termina con el último dato proporcionado, no repite el dato inicial como se muestra en la ecuación (1) anterior. Para mis propósitos, explicados más adelante, esta forma es intencional – en un estudio de terreno los datos de campo deben cerrar la figura, es decir, el ítem final debe ser igual al primero. En una aplicación de este tipo, cerrar automáticamente la figura como en la ecuación (1) ocultaría errores que deben ser evaluados.

  Los usuarios pueden preferir la forma mostrada en la ecuación (1) anterior, para fines distintos de la reducción de datos de la encuesta de la tierra. Para esos propósitos, durante el procesamiento simplemente reëvaluar el primer elemento de datos al final de la travesía, o proporcionar conjuntos de datos que repiten el primer elemento de datos como el último.

• Aquí es una función completa, trabajando Python:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• El argumento «array» anterior es un conjunto de coordenadas cartesianas $x,y$, es decir.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Observe acerca de este conjunto de datos que el primer elemento de datos se repite al final.

• Aquí hay una función de Python un poco más compleja que calcula tanto el área como la longitud del perímetro:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• De nuevo, este recordatorio: para los dos ejemplos de código anteriores, en aplicaciones distintas a la reducción de datos de estudios terrestres, el conjunto de datos proporcionado debe incluir una copia del primer dato como el último, es decir.

• Escogí Python para estos ejemplos porque un listado en Python maximiza el significado algorítmico al tiempo que minimiza el desorden.

• Las funciones anteriores pueden convertirse fácilmente a otros lenguajes, casi directamente – excepto la suma del perímetro mostrada arriba, que explota el hecho de que Python soporta números complejos. Para los lenguajes que no soportan números complejos, se puede crear el resultado del perímetro de esta manera:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formalmente, la longitud del perímetro es la suma de las magnitudes de los vectores:
  

  (3) Longitud del perímetro $\displaystyle P = \sum_{i=m}^{{n-1}{sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}$

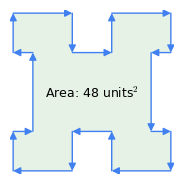
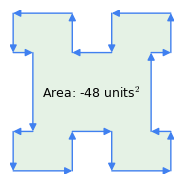Figura 1: Vectores en el sentido de las agujas del reloj vs. vectores en sentido contrario a las agujas del reloj

Aquí hay algunas propiedades importantes de este método:

• El vértice de origen elegido dentro del polígono es irrelevante para el cálculo del área o del perímetro, sólo que la figura sea cerrada, es decir.Es decir, que la última coordenada sea igual a la primera.
• «Regla de las agujas del reloj»: el orden de los vectores es significativo – si el perímetro se recorre en el sentido de las agujas del reloj, el resultado del área es positivo, si se recorre en sentido contrario, es negativo (Figura 1). Es esta propiedad del método la que resta el área de las inflexiones de una figura compleja como la de la Figura 1 – las «inflexiones» representan un recorrido en sentido contrario a las agujas del reloj dentro del polígono.
• Muchas aplicaciones de este método utilizan fuentes de datos originales consistentes en vectores polares (un ejemplo son las descripciones legales de los levantamientos topográficos), pero este método requiere coordenadas cartesianas. La conversión de coordenadas polares a cartesianas es trivial, pero es importante tener en cuenta este requisito.
• Además, para un cálculo preciso del área, el polígono descrito debe ser una figura cerrada – la última coordenada debe ser igual a la primera. Para las aplicaciones que utilizan datos de campo que consisten en vectores de longitud que se convierten posteriormente en forma cartesiana, es una buena idea comparar las coordenadas cartesianas iniciales y finales – deben ser iguales. Por ejemplo, los levantamientos de tierra más antiguos (antes de la era de la potencia de la computadora barata) regularmente fallan esta prueba.

Esta sección es una computadora de área/perímetro completamente funcional que puede procesar pares de datos de coordenadas cartesianas o polares introducidos, o descripciones legales de levantamiento. Sólo tiene que elegir un tipo de datos (coordenadas cartesianas x,y, coordenadas polares m,θ o una descripción legal del levantamiento) e introducir (o pegar) los datos en el área de entrada de datos de abajo. También puede seleccionar conjuntos de datos de muestra para familiarizarse y practicar.

Debido a los problemas de seguridad del navegador, para evitar teclear en exceso e importar cantidades significativas de datos desde otra fuente, los lectores tendrán que utilizar el portapapeles de su sistema. Sólo hay que copiar los datos en el portapapeles de la aplicación de origen, luego hacer clic en el área de entrada de datos de abajo y pulsar Crtl+A para seleccionar todo, Ctrl+V para pasar los datos de otro lugar y Ctrl+C para copiar los propios datos introducidos. La mayoría de los navegadores incluyen funciones de portapapeles como elementos de menú también.

Elija el tipo de datos:

Cartesianos (x,y)

polares (m,θ)

Descripción de la encuesta

Área de entrada de datos: Seleccionar todo: Ctrl+A | Copiar: Ctrl+C | Pegar: Ctrl+V

Área de gráficos:

Lo sentimos – su navegador no soporta la capacidad gráfica que requiere esta función –
considere instalar Google Chrome o Firefox.

Opciones:

Líneas

Flechas

Origen

Centro

Unidad de longitud:

Ancho de línea:

Invertir

Resultados:Seleccionar todo: Ctrl+A | Copiar: Ctrl+C | Pegar: Ctrl+V

El ordenador de área/perímetro tiene tres modos de entrada:

• Pares de coordenadas cartesianas (x,y):

  • Cada coordenada es una posición bidimensional con una parte horizontal (x) y otra vertical (y) (una coordenada cartesiana).
  • Las coordenadas no son acumulativas – cada una describe independientemente su ubicación.
  • Así que un cuadrado sería:
    • 0,0 (origen)
    • 0,100 (arriba)
    • 100,100 (derecha)
    • 100,0 (abajo)
    • 0,0 (vuelta al origen)
  

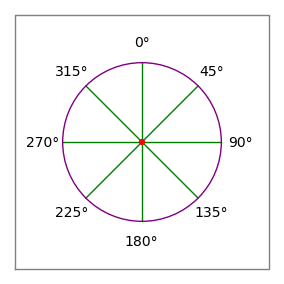  Figura 2: Rosa de los vientos

  • Las comas en el ejemplo anterior sólo sirven para agrupar los pares de datos para el lector – no tienen ningún significado para el analizador de datos del ordenador de la zona.
  • El analizador es lo suficientemente robusto como para que el ejemplo anterior pueda ser pegado en el área de entrada de datos del ordenador y funcione (pruébalo).
  • La única limitación es que los comentarios explicativos no pueden contener números.

• Pares de coordenadas polares (m,θ):

  • Cada coordenada consiste en una distancia y un ángulo en grados (un vector polar).
  • Los ángulos siguen la convención de la brújula – 0 grados es hacia arriba o «norte», 90 grados es hacia la derecha o «este» (Figura 2).
  • A diferencia de la forma cartesiana anterior, estas coordenadas son acumulativas – cada nuevo vector se suma a la posición actual.
  • Así que un cuadrado sería:
    • 100,0 (arriba)
    • 100,90 (derecha)
    • 100,180 (abajo)
    • 100,270 (vuelta al origen)
  • Como antes, este ejemplo funcionará si se pega en el área de entrada de datos del ordenador y se selecciona el modo polar.
  • Nótese sobre las coordenadas polares que el origen está implícito y prefijado en x = 0, y = 0.
  

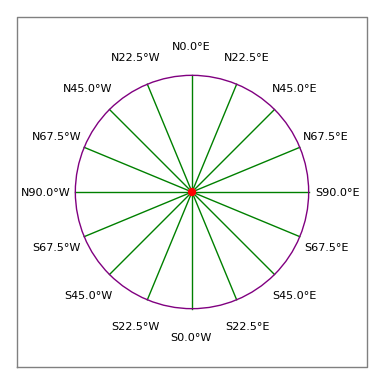  Figura 3: Rosa de los vientos de topógrafo

• Descripción legal:

  • Primero, una explicación de la relación entre la selección de «Unidades de longitud» y la visualización de resultados:
    • Para cada polígono, se calcula una lista de resultados de área utilizando un conjunto fijo de unidades de área comunes (pies2, metros2, etc.). Para que esta lista de áreas tenga sentido, las unidades de longitud de entrada deben ser conocidas.
    • En el modo cartesiano y polar, las entradas de datos no tienen unidades, por lo que el usuario elige qué unidades asignar a las longitudes. Así que cuando el usuario cambia las unidades de longitud, los valores de área cambian, las etiquetas de longitud cambian, pero los valores de longitud no lo hacen.
    • En el modo topográfico, la descripción legal contiene unidades de longitud (pies, metros, etc.) lo que significa que las unidades de longitud están predefinidas por la fuente. Así que cuando el usuario cambia las unidades de longitud, esto cambia las etiquetas y valores de longitud, no los valores de área.
  • El analizador de la descripción de la encuesta es, con mucho, el menos fiable de los tres métodos de análisis de datos – es más un experimento que un método de conversión de datos robusto.
  • Escribí este analizador descargando una serie de descripciones legales (que se proporcionan como ejemplos en la calculadora de arriba) y afinando el código del analizador hasta que todas pudieran ser decodificadas con éxito.

  Los criterios para el «éxito» eran que el resultado tuviera la misma área cuadrada que la descripción reclama, y que la figura «cerrara».

  • El término «cierre», y en particular el error de cierre, se utiliza en el trabajo topográfico para describir el grado en que el punto final de la travesía topográfica es igual al punto inicial. Esto rara vez es cierto en la realidad: los errores de cierre suelen ser consecuencia de errores en el trabajo de campo, y los levantamientos más antiguos, publicados antes de la llegada de la informática barata, suelen tener cierres bastante pobres, así como estimaciones muy inexactas de la superficie cuadrada.
  • Una descripción legal topográfica es una manera formal de describir una parcela de tierra – su forma y sintaxis ha surgido durante décadas por convenciones mutuamente aceptadas, algo arbitrarias, compartidas por los topógrafos.
  • Para este ordenador de área/perímetro los datos introducidos deben seguir ciertas convenciones estrictas a las que se adhieren algunas, pero no todas, las descripciones legales. Los elementos esenciales son:
    • La existencia de la frase «punto de inicio», que separa algún contenido preliminar del que describe las dimensiones de la parcela que se describe. Algunos documentos dicen «Punto de inicio real», otros dicen «Punto de inicio real» y otros dicen «Punto de inicio». Un analizador sintáctico exitoso necesita eliminar el contenido antes de esta frase y retener todo lo que hay después de ella.
    • Una serie de frases que describen un tipo especial de vector polar utilizado por los topógrafos:
      • La palabra «Norte» o «Sur», o su abreviatura «N» o «S».
      • Luego un ángulo expresado en grados, minutos y segundos.
      • Luego la palabra «Este» u «Oeste», o su abreviatura «E» u «W».
      • Luego una distancia.
      • Luego una unidad de distancia – pies, metros, etc.
  • Aquí hay algunos ejemplos diferentes de vectores topográficos de las descripciones legales de muestra:
    • N 2°0’0″ W – 63.50 pies
    • N90°00’00 «W A LO LARGO DE UNA LÍNEA PARALELA CON DICHA LÍNEA NORTE UNA DISTANCIA DE 6.00 PIES
    • Norte 0°06’O0″ Oeste una distancia de 554.86 pies
    • S. 22 grados 41′ 55″ E. 174.10 pies
  • Nótese sobre los ejemplos anteriores que todos tienen diferente sintaxis. Hay muchas descripciones legales en existencia que este analizador no decodificará con éxito, sólo porque no he tratado de incorporar su sintaxis. Pero es importante añadir que un analizador verdaderamente robusto para la multitud de descripciones legales existentes tendría que ser tan inteligente como Watson.
  • Los usuarios de este ordenador de áreas/perímetros pueden querer evitar enviar descripciones legales en texto plano y esperar que el analizador lo resuelva. Para hacer entradas directas a mano (o para crear una lista de travesías en otro lugar para la importación), utilice esta convención:
    • Recuerde que una entrada de travesía aceptable consiste en la palabra «Norte» o «Sur», o la letra «N» o «S», seguida de hasta tres números que proporcionan grados, minutos y segundos de ángulo, seguida de la palabra «Este» u «Oeste» o la letra «E» o «W», seguida de una distancia, seguida de una unidad de distancia.
    • Así que una entrada aceptable sería «N 30 15 45 W 100 pies», lo que significa una travesía de 100 pies que apunta a 30 grados, 15 minutos y 45 segundos al Oeste del Norte (es decir, aproximadamente 330 grados de la brújula, véase la figura 3).
    • Las entradas de minutos y segundos pueden omitirse si son iguales a cero, o si la entrada está en grados decimales, o grados y minutos decimales.
  • No es difícil convertir una descripción legal impresa en este tipo de entradas, y hay varias formas de detectar errores. Después de haber introducido todas las travesías, si la figura no tiene ningún error de cierre y reporta la misma área cuadrada que el original, lo más probable es que las entradas sean correctas (o que tengan los mismos errores que la descripción original).
  • Después de introducir una descripción legal de esta manera, si hay un error de cierre inaceptable o el área cuadrada es incorrecta, recuerde que los datos originales podrían estar equivocados. Hay cualquier número de descripciones legales en existencia que nunca se han comprobado con un método informático como este, y que nunca fueron correctas.

Mientras navega por los ejemplos cartesianos (x,y), fíjese en la relación de área y perímetro de las diferentes formas. El «polígono de forma extraña» tiene una relación intermedia, el círculo tiene la relación más pequeña y el espacio de Hilbert tiene, con mucho, la relación más grande. Esta relación se extiende a dimensiones superiores, donde se sabe que una esfera tiene el mayor volumen por superficie.

Sobre el ejemplo del círculo – es un «círculo unitario», un círculo con un radio de uno. Para el ejemplo proporcionado, el área se aproxima a $\pi$ y el perímetro se aproxima a $2\pi$, los valores correctos para un círculo unitario. Para que esos valores sean más que aproximaciones, para que sean exactamente iguales $\pi$ y $2\pi$, el número de lados del polígono tendría que ser infinito. Decidí no hacerlo 🙂

El ejemplo del espacio de Hilbert se generó utilizando un algoritmo de Sage con una elección de orden modesta (para evitar generar demasiados datos). En principio un espacio de Hilbert puede tener una relación infinita entre perímetro y área en dos dimensiones, o entre superficie y volumen en tres dimensiones. Para ver lo complejo que puede llegar a ser un espacio de Hilbert, haga clic aquí para ver un espacio de Hilbert de orden 7.

Nótese en el ejemplo de Hilbert que el área calculada es cercana a 1/2 para una superficie de 1×1. Idealmente, sin la necesidad de convertir una figura de línea en una figura de área y con el algoritmo correcto, el área de la superficie sería exactamente 1/2 la de un cuadrado de las mismas dimensiones.

El modo de entrada polar es más o menos igual a los gráficos de Tortuga, si uno sustituye cero grados por «arriba», 90 grados por «derecha», etc., y si cada secuencia de giro y movimiento se colapsa en un comando. El uso del modo de entrada polar es una manera fácil de construir a mano una forma compleja, porque las distancias y los ángulos son más fáciles de seguir que las coordenadas cartesianas.

La primera vez que utilicé el método de cálculo del área de levantamiento topográfico descrito anteriormente fue hace años, cuando vivía en la zona rural de Oregón, rodeado de personas que necesitaban conocer el área y el perímetro de sus propiedades. Me encontré con muchos ejemplos chocantes en los que los agentes inmobiliarios engañaban descaradamente a las personas que no tenían forma de averiguar lo que estaba pasando. En numerosas ocasiones, calculé una superficie a partir de una descripción legal, sólo para descubrir que la afirmación de la escritura de garantía sobre la superficie en acres era tremendamente inexacta, y siempre superior a la realidad.

En una ocasión me pidieron que dividiera una propiedad en dos secciones iguales y creara descripciones legales para cada una. Como tenía un Apple II recién adquirido (que tenía la capacidad de procesamiento de un sacapuntas moderno), esto fue muy fácil, pero mientras trabajaba me di cuenta de que el total de acres estaba fuera de lugar por unos tres acres, aproximadamente el 25% del total. Me enfrenté a la compañía de títulos, que descaradamente me respondió: «¿Ves aquí, donde la escritura dice ‘más o menos’?»

En otra ocasión comencé la compra de un terreno, pero prevenido por la experiencia anterior, cuando recibí la póliza del título decidí introducir su descripción legal en mi programa para ver si la reclamación de acres era exacta. Pero, para mi horror, descubrí que todas las pólizas de título de las parcelas de esa sección tenían la misma descripción legal: la de la primera propiedad topografiada. Resulta que la empresa promotora decidió ahorrarse dinero topografiando sólo una de las docenas de parcelas que se ofrecían a la venta, e incluir esa descripción legal en todas las pólizas del título. Después de discutir con la compañía de títulos y con el promotor, tratando de persuadirles de que pagaran por los estudios para que las descripciones legales no fueran ficticias, me rendí y decidí no comprar el terreno. Fue como descubrir cómo se hace la salchicha: es posible saber demasiado.

• 04.15.2013 Versión 1.3. Añadida una explicación detallada del formato de datos por defecto, es decir, listas que repiten el primer punto de datos como el último.
• 03.24.2013 Versión 1.2. Optimizado aún más el analizador sintáctico de descripciones de encuestas, añadido más campos de datos de resultados.
• 03.23.2013 Versión 1.1. Mejorado el analizador de descripciones legales para tratar más tipos de descripciones, añadido selector de unidades de longitud y una lista de resultados de áreas en unidades comunes.
• 03.22.2013 Versión 1.0. Versión pública inicial.