Rovnice SHM
Považujte kvádr připevněný k pružině na stole bez tření (obrázek \(\PageIndex{3}\)). Rovnovážná poloha (poloha, kdy pružina není ani natažená, ani stlačená) je označena jako x = 0 . V rovnovážné poloze je čistá síla nulová.
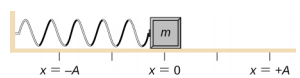
Pracuje se s kvádrem tak, aby byl vytažen do polohy x = + A, a poté je uvolněn z klidu. Maximální poloha x (A) se nazývá amplituda pohybu. Kvádr začne kmitat v SHM mezi x = + A a x = -A, kde A je amplituda pohybu a T je perioda kmitání. Perioda je doba jednoho kmitání. Obrázek \(\PageIndex{4}\) ukazuje pohyb kvádru, který po uvolnění dokončí jeden a půl oscilace.
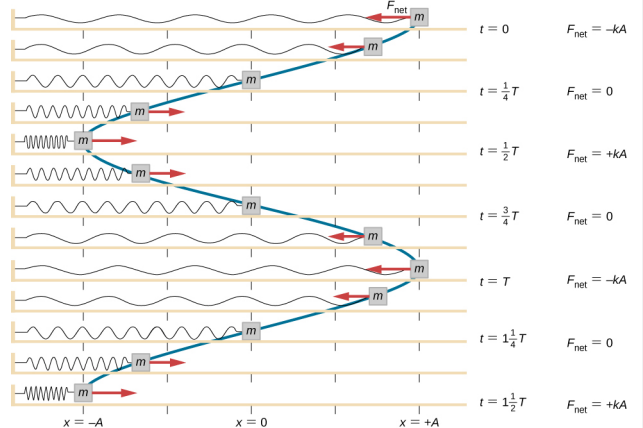
\
Rovnice pro polohu jako funkci času \(x(t) = A\cos( \omega t)\) je vhodná pro modelování dat, kde poloha kvádru v počátečním čase t = 0,00 s má amplitudu A a počáteční rychlost je nulová. Při experimentálních datech se často stává, že poloha tělesa v počátečním čase t = 0,00 s není rovna amplitudě a počáteční rychlost není nulová. Uvažujme 10sekundová data nasbíraná studentem v laboratoři, která jsou zobrazena na obrázku \(\PageIndex{6}\).
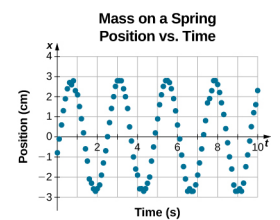
Údaje na obrázku \(\PageIndex{6}\) lze stále modelovat pomocí periodické funkce, jako je kosinová funkce, ale funkce je posunuta doprava. Tento posun se nazývá fázový posun a obvykle se znázorňuje řeckým písmenem phi (\(\phi\)). Rovnice polohy jako funkce času pro kvádr na pružině má tvar
\
Toto je zobecněná rovnice pro SHM, kde t je čas měřený v sekundách, \(\omega\) je úhlová frekvence s jednotkami inverzních sekund, A je amplituda měřená v metrech nebo centimetrech a \(\phi\) je fázový posun měřený v radiánech (obrázek \(\PageIndex{7}\). Je třeba poznamenat, že vzhledem k tomu, že funkce sinus a kosinus se liší pouze fázovým posunem, lze tento pohyb modelovat pomocí funkce kosinus nebo sinus.
Rychlost hmoty na pružině, která kmitá v SHM, lze zjistit derivací polohové rovnice:
\
Protože sinusová funkce kmitá mezi -1 a +1, maximální rychlost je amplituda krát úhlová frekvence, vmax = A\(\omega\). Maximální rychlost nastává v rovnovážné poloze (x = 0), když se těleso pohybuje směrem k x = + A. Maximální rychlost v záporném směru nastává v rovnovážné poloze (x = 0), když se těleso pohybuje směrem k x = -A, a je rovna -vmax.
Zrychlení tělesa na pružině lze zjistit derivací rychlosti v čase:
\
.