Equations of SHM
摩擦のないテーブルの上に、ばねに取り付けられたブロックがあるとします(図㊦)。 平衡位置(バネが伸びも縮みもしない位置)をx=0とします。 平衡位置では正味の力は0になる
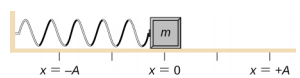
バネが伸びも縮みもしない平衡位置をx=0とする。
ブロックに作用してx=+Aの位置まで引き抜き、静止状態を解除する。 xの最大位置(A)を運動の振幅という。 ブロックはx=+Aからx=-Aの間でSHM振動を開始し、Aは運動の振幅、Tは振動の周期である。 周期は1回の振動の時間である。 図⑭は、ブロックがリリース後1.5揺動を終えたときの様子を示しています。 バネの一端にブロックを取り付け、摩擦のないテーブルの上に置きます。 バネのもう一方の端は壁に固定されています。 正味の力がゼロになる平衡位置をx=0 mとする。ブロックに仕事を与えてx=+Aまで引き伸ばし、ブロックを静止状態から解放する。 ブロックは x = + A と x = – A の間で振動する。
位置を時間の関数で表す式 \(x(t) = Acos( \omega t)\) は、初期時刻t = 0.00 sにおけるブロックの位置が振幅A、初速度0というデータをモデル化するには良い式である。 実験データを取る場合、初期時刻t=0.00 sにおける質量の位置が振幅と等しくなく、初速度が0でないことがよくある。 図⑭のような、ある生徒が実験室で集めた10秒間のデータを考えてみましょう。 研究室の学生が音波距離計で測定した、バネに取り付けたブロックの位置を示すデータです。 データは時刻t=0.00sから収集されているが、初期位置は位置x≒-0.80cm≠3.00cm付近であり、初期位置は振幅x0=+Aにはならない。速度とは位置の時間微分で、位置と時間のグラフ上のある点での傾きである。
図のデータもやはりコサイン関数のような周期関数でモデル化できますが、関数が右側にずれています。 このずれを位相シフトといい、通常ギリシャ文字のphiで表します(˶‾᷄ -̫ ‾᷅˵ )。 ここで、tは秒単位で表される時間、 \は逆秒単位の角周波数、Aはメートルまたはセンチメートル単位の振幅、 \はラジアン単位の位相シフトです(図(Ⓐ))。 なお、サイン関数とコサイン関数の違いは位相のずれだけなので、この運動はコサイン関数でもサイン関数でもモデル化することができます。
SHMで振動するバネ上の質量の速度は、位置の式を微分することで求められる。
サイン関数は-1から+1まで振動するので、最大速度は振幅×角周波数でvmax = AΘ(\omega) 質量がx=+Aに向かう平衡位置(x=0)で最大速度、質量がx=-Aに向かう平衡位置(x=0)で負方向の最大速度は-vmaxに等しい。
ばね上の質量の加速度は、速度の時間微分をとることにより求められる。