Logistická regrese

Logistická regrese (také známá jako logitová regrese nebo logitový model) byla vyvinuta statistikem Davidem Coxem v roce 1958 a jedná se o regresní model, kde proměnná odpovědi Y je kategoriální. Logistická regrese nám umožňuje odhadnout pravděpodobnost kategorické odpovědi na základě jedné nebo více predikčních proměnných (X). Umožňuje říci, že přítomnost prediktoru zvyšuje (nebo snižuje) pravděpodobnost daného výsledku o určité procento. Tento návod se zabývá případem, kdy je Y binární, tj. kdy může nabývat pouze dvou hodnot, „0“ a „1“, které představují výsledky, jako je úspěch/neúspěch, výhra/prohra, živý/mrtvý nebo zdravý/nemocný. Případy, kdy má závislá proměnná více než dvě kategorie výsledků, lze analyzovat pomocí multinomické logistické regrese nebo, pokud je více kategorií uspořádáno, pomocí ordinální logistické regrese. Oblíbenou metodou pro klasifikaci více tříd se však stala diskriminační analýza, takže náš další tutoriál se zaměří na tuto techniku pro tyto případy.

tl;dr

Tento tutoriál slouží jako úvod do logistické regrese a zahrnuje1:

1. Požadavky na replikaci: Co budete potřebovat k reprodukci analýzy v tomto tutoriálu
2. Proč logistická regrese: Proč používat logistickou regresi?
3. Příprava našich dat: Příprava našich dat pro modelování
4. Jednoduchá logistická regrese:
5. Vícenásobná logistická regrese: Předpovídání pravděpodobnosti odpovědi Y s jedinou predikční proměnnou X
6. Vícenásobná logistická regrese: Předpovídání pravděpodobnosti odpovědi Y s více predikčními proměnnými
7. Vyhodnocení modelu & diagnostika: Jak dobře model odpovídá datům? Které prediktory jsou nejdůležitější? Jsou předpovědi přesné?“

Požadavky na replikaci

Tento výukový program využívá především data Default, která poskytuje balíček ISLR. Jedná se o simulovaný soubor dat obsahující informace o deseti tisících zákaznících, například zda zákazník nesplácí, je student, průměrný zůstatek, který zákazník nese, a příjem zákazníka. Použijeme také několik balíčků, které poskytují funkce pro manipulaci s daty, vizualizaci, modelování potrubí a funkce pro úpravu výstupů modelu.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Proč logistická regrese

Lineární regrese není vhodná v případě kvalitativní odpovědi. Proč tomu tak není? Předpokládejme, že se snažíme předpovědět zdravotní stav pacientky na pohotovosti na základě jejích příznaků. V tomto zjednodušeném příkladu existují tři možné diagnózy: mrtvice, předávkování drogami a epileptický záchvat. Mohli bychom uvažovat o kódování těchto hodnot jako kvantitativní proměnné odpovědi, Y , takto:

Pomocí tohoto kódování by bylo možné použít metodu nejmenších čtverců k sestavení lineárního regresního modelu pro předpověď Y na základě souboru prediktorů . Bohužel toto kódování implikuje pořadí výsledků, přičemž předávkování drogami řadí mezi mrtvici a epileptický záchvat a trvá na tom, že rozdíl mezi mrtvicí a předávkováním drogami je stejný jako rozdíl mezi předávkováním drogami a epileptickým záchvatem. V praxi neexistuje žádný zvláštní důvod, proč by tomu tak mělo být. Lze například zvolit stejně rozumné kódování,

které by znamenalo zcela jiný vztah mezi těmito třemi stavy. Každé z těchto kódování by vedlo k zásadně odlišným lineárním modelům, které by v konečném důsledku vedly k odlišným souborům předpovědí na základě testovacích pozorování.

Významnější pro naše data je, že pokud se snažíme klasifikovat zákazníka jako neplatiče s vysokým a nízkým rizikem na základě jeho zůstatku, mohli bychom použít lineární regresi; levý obrázek níže však ilustruje, jak by lineární regrese předpovídala pravděpodobnost nesplácení. Bohužel pro zůstatky blízké nule předpovídáme zápornou pravděpodobnost nesplácení; pokud bychom předpovídali pro velmi velké zůstatky, dostali bychom hodnoty větší než 1. Tyto předpovědi nejsou rozumné, protože skutečná pravděpodobnost nesplácení, bez ohledu na zůstatek kreditní karty, musí samozřejmě spadat mezi 0 a 1.

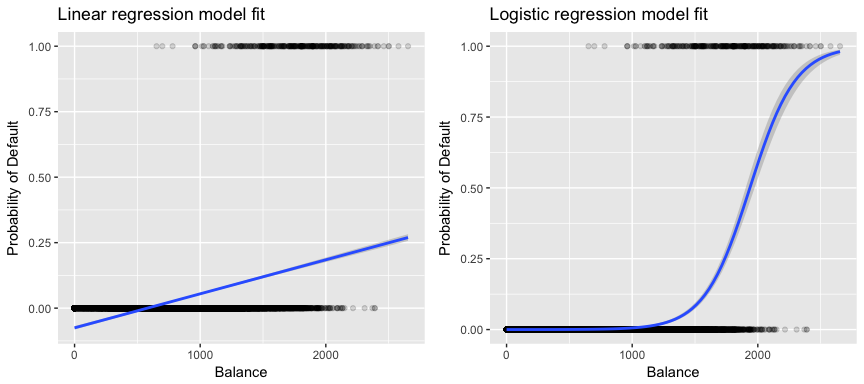
Abychom se tomuto problému vyhnuli, musíme modelovat p(X) pomocí funkce, která dává výstupy mezi 0 a 1 pro všechny hodnoty X. Tomuto popisu vyhovuje mnoho funkcí. V logistické regresi používáme logistickou funkci, která je definována v rovnici 1 a znázorněna na obrázku vpravo nahoře.

Příprava našich dat

Stejně jako v učebnici regrese rozdělíme naše data na trénovací (60 %) a testovací (40 %) množinu dat, abychom mohli posoudit, jak dobře náš model funguje na množině dat mimo vzorek.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Jednoduchá logistická regrese

Na základě průměrného zůstatku, který zákazník nese, sestavíme logistický regresní model, abychom předpověděli pravděpodobnost selhání zákazníka. Funkce glm fituje zobecněné lineární modely, což je třída modelů, která zahrnuje logistickou regresi. Syntaxe funkce glm je podobná syntaxi funkce lm s tím rozdílem, že musíme předat argument family = binomial, abychom R řekli, že má spustit logistickou regresi, a ne jiný typ zobecněného lineárního modelu.

model1 <- glm(default ~ balance, family = "binomial", data = train)

V pozadí funkce glm, používá k fitování modelu maximální věrohodnost. Základní intuice použití maximální věrohodnosti pro fitování modelu logistické regrese je následující: hledáme odhady pro a takové, aby předpovězená pravděpodobnost selhání pro každého jednotlivce pomocí rovnice 1 co nejpřesněji odpovídala pozorovanému stavu selhání jednotlivce. Jinými slovy, snažíme se najít a takové, aby dosazení těchto odhadů do modelu pro p(X), uvedeného ve vzorci 1, dávalo číslo blízké jedné pro všechny jednotlivce, kteří selhali, a číslo blízké nule pro všechny jednotlivce, kteří selhali. Tuto intuici lze formalizovat pomocí matematické rovnice zvané věrohodnostní funkce:

Odhady a jsou zvoleny tak, aby maximalizovaly tuto věrohodnostní funkci. Maximální věrohodnost je velmi obecný přístup, který se používá k fitování mnoha nelineárních modelů, které budeme zkoumat v dalších tutoriálech. Výsledkem je pravděpodobnostní křivka ve tvaru písmene S znázorněná níže (všimněte si, že pro vykreslení přímky shody logistické regrese musíme naši proměnnou odpovědi převést na binární kódovanou proměnnou).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Podobně jako u lineární regrese můžeme model posoudit pomocí summary nebo glance. Všimněte si, že formát výstupu koeficientů je podobný tomu, který jsme viděli u lineární regrese; údaje o dobré shodě v dolní části summary se však liší. Později se tomu budeme věnovat podrobněji, ale všimněte si jen, že vidíte slovo odchylka. Odchylka je obdobou výpočtu součtu čtverců v lineární regresi a je mírou nedostatečné shody s daty v logistickém regresním modelu. Nulová odchylka představuje rozdíl mezi modelem pouze s interceptem (což znamená „bez prediktorů“) a nasyceným modelem (modelem s teoreticky dokonalou shodou). Cílem je, aby odchylka modelu (označovaná jako zbytková odchylka) byla nižší; menší hodnoty naznačují lepší shodu. V tomto ohledu poskytuje nulový model výchozí hodnotu, na níž lze porovnávat modely s prediktory.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Ohodnocení koeficientů

Níže uvedená tabulka uvádí odhady koeficientů a související informace, které jsou výsledkem fitování logistického regresního modelu za účelem předpovědi pravděpodobnosti selhání = Ano s použitím rovnováhy. Mějte na paměti, že odhady koeficientů z logistické regrese charakterizují vztah mezi prediktorem a proměnnou odpovědi na logaritmické stupnici (podrobněji viz kap. 3 ISLR1). Vidíme tedy, že ; to znamená, že zvýšení zůstatku je spojeno se zvýšením pravděpodobnosti selhání. Přesněji řečeno, zvýšení zůstatku o jednu jednotku je spojeno se zvýšením logaritmické pravděpodobnosti selhání o 0,0057 jednotky.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Koeficient zůstatku můžeme dále interpretovat jako – na každý jeden dolar zvýšení neseného měsíčního zůstatku se pravděpodobnost selhání zákazníka zvýší o faktor 1. To znamená, že se pravděpodobnost selhání zvýší o jeden dolar.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Mnoho aspektů výstupu koeficientu je podobných těm, které byly diskutovány u výstupu lineární regrese. Například můžeme měřit intervaly spolehlivosti a přesnost odhadů koeficientů výpočtem jejich standardních chyb. Například má p-hodnotu < 2e-16, která naznačuje statisticky významný vztah mezi neseným zůstatkem a pravděpodobností selhání. Standardní chyby můžeme také použít k získání intervalů spolehlivosti, jak jsme to udělali v učebnici lineární regrese:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Tvorba předpovědí

Po odhadu koeficientů je jednoduché vypočítat pravděpodobnost selhání pro libovolný daný zůstatek na kreditní kartě. Matematicky pomocí odhadů koeficientů z našeho modelu předpovídáme, že pravděpodobnost selhání pro jednotlivce se zůstatkem 1 000 USD je menší než 0,5 %

Pravděpodobnost selhání můžeme předpovědět v R pomocí funkce predict (nezapomeňte uvést type = "response"). Zde porovnáme pravděpodobnost selhání na základě zůstatků ve výši 1000 USD a 2000 USD. Jak vidíte, s pohybem zůstatku z 1000 USD na 2000 USD se pravděpodobnost selhání výrazně zvyšuje, a to z 0,5 % na 58 %!“

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Pomocí logistického regresního modelu lze také použít kvalitativní prediktory. Jako příklad lze uvést model, který využívá proměnnou student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Koeficient spojený s student = Yes je kladný a související p-hodnota je statisticky významná. To naznačuje, že studenti mají tendenci mít vyšší pravděpodobnost selhání než nestudenti. Ve skutečnosti tento model naznačuje, že student má téměř dvakrát vyšší pravděpodobnost selhání než nestudenti. V další části však uvidíme proč.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Vícená logistická regrese

Náš model můžeme také rozšířit, jak je vidět z rovnice. 1 tak, že můžeme předpovědět binární odpověď pomocí vícenásobných prediktorů, kde je p prediktorů:

Pokračujme a sestavme model, který předpovídá pravděpodobnost selhání na základě proměnných zůstatek, příjem (v tisících dolarů) a status studenta. Zde se objevuje překvapivý výsledek. Hodnoty p spojené se zůstatkem a statusem studenta=Ano jsou velmi malé, což naznačuje, že každá z těchto proměnných je spojena s pravděpodobností selhání. Koeficient pro proměnnou student je však záporný, což naznačuje, že studenti mají menší pravděpodobnost selhání než nestudenti. Naproti tomu koeficient pro proměnnou student v modelu 2, kde jsme předpovídali pravděpodobnost selhání pouze na základě statusu studenta, naznačuje, že studenti mají větší pravděpodobnost selhání. Co z toho vyplývá?“

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Vysvětlení tohoto rozporu poskytuje pravý panel níže uvedeného obrázku. Proměnné student a zůstatek jsou korelované. Studenti mají tendenci držet vyšší úroveň dluhu, což je zase spojeno s vyšší pravděpodobností selhání. Jinými slovy, studenti mají s větší pravděpodobností velké zůstatky na kreditních kartách, které, jak víme z levého panelu níže uvedeného obrázku, bývají spojeny s vysokou mírou selhání. Ačkoli tedy jednotlivý student s daným zůstatkem na kreditní kartě bude mít tendenci mít nižší pravděpodobnost selhání než nestudent se stejným zůstatkem na kreditní kartě, skutečnost, že studenti jako celek mají tendenci mít vyšší zůstatky na kreditních kartách, znamená, že celkově mají studenti tendenci selhávat častěji než nestudenti. To je důležitý rozdíl pro společnost vydávající kreditní karty, která se snaží určit, komu má úvěr nabídnout. Student je rizikovější než nestudent, pokud nejsou k dispozici informace o jeho zůstatku na kreditní kartě. Tento student je však méně rizikový než nestudent se stejným zůstatkem na kreditní kartě!“

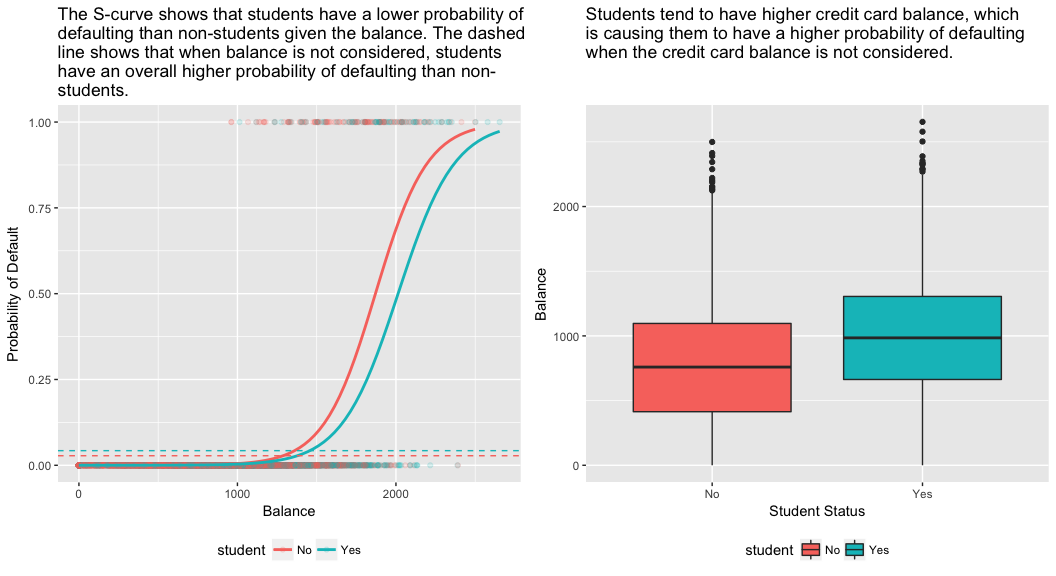
Tento jednoduchý příklad ilustruje nebezpečí a jemnosti spojené s prováděním regresí zahrnujících pouze jeden prediktor, když mohou být relevantní i jiné prediktory. Výsledky získané pomocí jednoho prediktoru mohou být zcela odlišné od výsledků získaných pomocí více prediktorů, zejména pokud mezi prediktory existuje korelace. Tento jev se nazývá confounding.

V případě více predikčních proměnných někdy chceme pochopit, která proměnná má největší vliv na predikci proměnné odpovědi (Y). To můžeme provést pomocí varImp z balíčku caret. Zde vidíme, že rovnováha je s velkým náskokem nejdůležitější, zatímco status studenta je méně důležitý, následovaný příjmem (který se stejně ukázal jako nevýznamný (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Stejně jako dříve můžeme pomocí tohoto modelu snadno provádět predikce. Například student se zůstatkem na kreditní kartě 1 500 USD a příjmem 40 000 USD má odhadovanou pravděpodobnost selhání

Nestudent se stejným zůstatkem a příjmem má odhadovanou pravděpodobnost selhání

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Tak vidíme, že pro daný zůstatek a příjem (i když příjem je nevýznamný) má student přibližně poloviční pravděpodobnost selhání než nestudent.

Vyhodnocení modelu &Diagnostika

Dosud byly sestaveny tři logistické regresní modely a zkoumány jejich koeficienty. Některé zásadní otázky však zůstávají. Jsou tyto modely vůbec dobré? Jak dobře model odpovídá údajům? A jak přesné jsou předpovědi na souboru dat mimo vzorek?“

Goodness-of-Fit

V učebnici lineární regrese jsme viděli, jak nás F-statistika a upravené , a reziduální diagnostiky informují o tom, jak dobře model odpovídá datům. Zde se podíváme na několik způsobů, jak posoudit dobrou shodu našich logitových modelů.

Test poměru věrohodnosti

Napřed můžeme použít test poměru věrohodnosti, abychom posoudili, zda naše modely lépe vyhovují. Přidání predikčních proměnných do modelu téměř vždy zlepší shodu modelu (tj. zvýší logaritmickou pravděpodobnost a sníží odchylku modelu ve srovnání s nulovou odchylkou), ale je nutné otestovat, zda je pozorovaný rozdíl ve shodě modelu statisticky významný. K provedení tohoto testu můžeme použít anova. Výsledky ukazují, že ve srovnání s model1 snižuje model3 reziduální odchylku o více než 13 (nezapomeňte, že cílem logistické regrese je najít model, který minimalizuje reziduální odchylku). A co je důležitější, toto zlepšení je statisticky významné na p = 0,001. To naznačuje, že model3 skutečně poskytuje lepší přizpůsobení modelu.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Na rozdíl od lineární regrese s běžným odhadem nejmenších čtverců neexistuje statistika, která by vysvětlovala podíl rozptylu závislé proměnné, který je vysvětlen prediktory. Existuje však řada pseudometrik, které by mohly být cenné. Nejvýznamnější je McFaddenova , která je definována jako

kde je hodnota logaritmické věrohodnosti pro fitovaný model a je logaritmická věrohodnost pro nulový model pouze s interceptem jako prediktorem. Míra se pohybuje v rozmezí od 0 do necelé 1, přičemž hodnoty bližší nule znamenají, že model nemá žádnou prediktivní sílu. Na rozdíl od lineární regrese však modely málokdy dosahují vysoké McFaddenovy . Ve skutečnosti podle McFaddenových vlastních slov modely s McFaddenovou pseudohodnotou představují velmi dobrou shodu. Hodnoty McFaddenova pseudohodnoty pro naše modely můžeme posoudit pomocí:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Vidíme, že model 2 má velmi nízkou hodnotu potvrzující jeho špatnou shodu. Modely 1 a 3 však mají mnohem vyšší hodnoty, což naznačuje, že vysvětlují dostatečné množství rozptylu ve výchozích datech. Dále vidíme, že model 3 zlepšuje jen velmi mírně.

Vyhodnocení reziduí

Mějte na paměti, že logistická regrese nepředpokládá, že rezidua jsou normálně rozdělena ani že rozptyl je konstantní. Deviance reziduí je však užitečná pro určení, zda jednotlivé body modelu dobře neodpovídají. Zde můžeme fitovat standardizovaná odchylková rezidua, abychom zjistili, kolik z nich přesahuje 3 směrodatné odchylky. Nejprve extrahujeme několik užitečných kousků výsledků modelu pomocí augment a poté přistoupíme k vykreslení.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)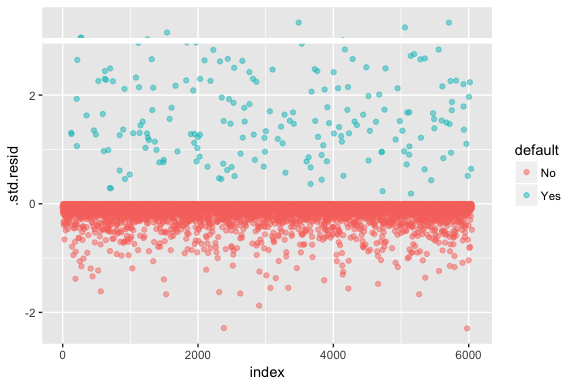

Ta standardizovaná rezidua, která přesahují 3, představují možné odlehlé hodnoty a mohou si zasloužit větší pozornost. Tato rezidua můžeme filtrovat, abychom se na ně podívali blíže. Vidíme, že všechna tato pozorování představují zákazníky, kteří neplnili své závazky s rozpočty, které jsou mnohem nižší než u běžných neplatičů.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Podobně jako u lineární regrese můžeme také identifikovat vlivná pozorování pomocí hodnot Cookovy vzdálenosti. Zde identifikujeme 5 největších hodnot.

plot(model1, which = 4, id.n = 5)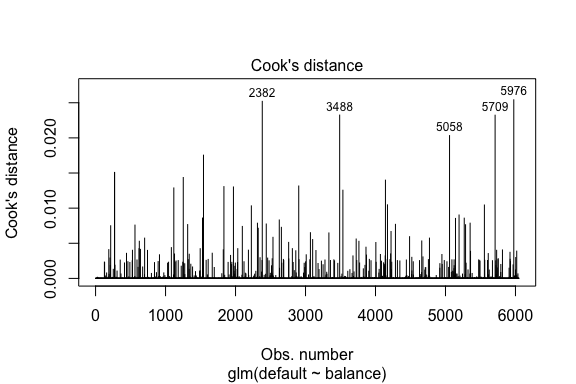

A i ty můžeme dále zkoumat. Zde vidíme, že mezi pět nejvlivnějších bodů patří:

• ti zákazníci, kteří nespláceli s velmi nízkými zůstatky, a
• dva zákazníci, kteří nespláceli, ale měli zůstatky nad 2 000 USD

To znamená, že pokud bychom tato pozorování odstranili (nedoporučujeme), tvar, umístění a interval spolehlivosti naší S-křivky logistické regrese by se pravděpodobně posunuly.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Validace predikovaných hodnot

Míra klasifikace

Při vývoji modelů pro predikci je nejkritičtější metrika týkající se toho, jak dobře si model vede při predikci cílové proměnné na pozorováních mimo vzorek. Nejprve musíme odhadnuté modely použít k předpovědi hodnot na našem trénovacím souboru dat (train). Při použití predict nezapomeňte uvést type = response, aby predikce vracela pravděpodobnost výchozího stavu.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Nyní můžeme porovnat predikovanou cílovou proměnnou oproti pozorovaným hodnotám pro každý model a zjistit, který si vede nejlépe. Můžeme začít pomocí matice záměny, což je tabulka, která popisuje klasifikační výkonnost každého modelu na testovacích datech. Každý kvadrant tabulky má důležitý význam. V tomto případě „Ne“ a „Ano“ v řádcích představují, zda zákazníci neplnili své závazky, nebo ne. „FALSE“ a „TRUE“ ve sloupcích představují, zda jsme předpověděli, že zákazníci nesplní své závazky, nebo ne.

• true positives (pravý dolní kvadrant): jedná se o případy, kdy jsme předpověděli, že zákazník nesplní své závazky, a on je splnil.
• true negatives (levý horní kvadrant):
• falešně pozitivní (pravý horní kvadrant): v těchto případech jsme předpověděli, že zákazník nesplní své závazky, a zákazník je nesplnil: Předpověděli jsme, že ano, ale zákazník ve skutečnosti neplnil své závazky. (Známé také jako „chyba typu I“.)
• falešně negativní (levý dolní kvadrant): Předpověděli jsme, že ne, ale skutečně došlo k selhání. (Známé také jako „chyba typu II“.)

Výsledky ukazují, že model1 a model3 jsou si velmi podobné. Z předpovězených pozorování je 96 % pravdivě negativních a přibližně 1 % pravdivě pozitivních. Oba modely mají chybu typu II menší než 3 %, kdy model předpovídá, že zákazník nesplní své závazky, ale ve skutečnosti je nesplnil. A oba modely mají chybu typu I menší než 1 %, kdy modely předpovídají, že zákazník nesplácí, ale nikdy nesplnil. model2 Výsledky se nápadně liší; tento model přesně předpovídá zákazníky, kteří nesplácejí (což je výsledek toho, že 97 % dat jsou zákazníci, kteří nesplácejí), ale nikdy ve skutečnosti nepředpovídá ty zákazníky, kteří nesplácejí!“

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Chceme také pochopit míru chybné klasifikace (neboli chyby) (nebo bychom to mohli převrátit na míru přesnosti). Mezi modely 1 a 3 nevidíme velké zlepšení, a přestože model 2 má nízkou chybovost, nezapomeňte, že nikdy přesně nepředpovídá zákazníky, kteří skutečně neplní své závazky.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Nějaké další poznatky můžeme získat, když se podíváme na hrubé hodnoty (ne procenta) v naší matici záměny. Podívejme se pro ilustraci na model 1. Vidíme, že existuje celkem zákazníků, kteří nespláceli. Z celkového počtu selhání nebyla předpovězena. Případně můžeme říci, že pouze z výskytu selhání bylo předpovězeno – to je známé jako přesnost (známá také jako citlivost) našeho modelu. Ačkoli je tedy celková chybovost nízká, je nízká i míra přesnosti, což není dobré!“

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

U klasifikačních modelů se při charakteristice výkonnosti modelu setkáte také s pojmy citlivost a specifičnost. Jak bylo uvedeno výše, citlivost je synonymem přesnosti. Specificita je však procento správně identifikovaných neplatičů, zde (přesnost je zde do značné míry dána tím, že 97 % pozorování v našich datech jsou neplatiči). Význam mezi citlivostí a specifičností závisí na kontextu. V tomto případě bude společnost vydávající kreditní karty pravděpodobně více dbát na citlivost, protože chce snížit své riziko. Proto jim může více záležet na vyladění modelu tak, aby se zlepšila jejich citlivost/přesnost.

Přijímací operační charakteristika (ROC) je vizuální měřítko výkonnosti klasifikátoru. Pomocí podílu pozitivních datových bodů, které jsou správně považovány za pozitivní, a podílu negativních datových bodů, které jsou mylně považovány za pozitivní, vytváříme graf, který ukazuje kompromis mezi mírou, s jakou lze něco správně předpovědět, s mírou, s jakou lze něco nesprávně předpovědět. V konečném důsledku nás zajímá plocha pod křivkou ROC neboli AUC. Tato metrika se pohybuje v rozmezí od 0,50 do 1,00 a hodnoty nad 0,80 naznačují, že model odvádí dobrou práci při rozlišování mezi dvěma kategoriemi, které tvoří naši cílovou proměnnou. Můžeme porovnat hodnoty ROC a AUC pro modely 1 a 2, které vykazují výrazný rozdíl ve výkonnosti. Rozhodně chceme, aby naše grafy ROC vypadaly spíše jako u modelu 1 (vlevo) než u modelu 2 (vpravo)!“

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()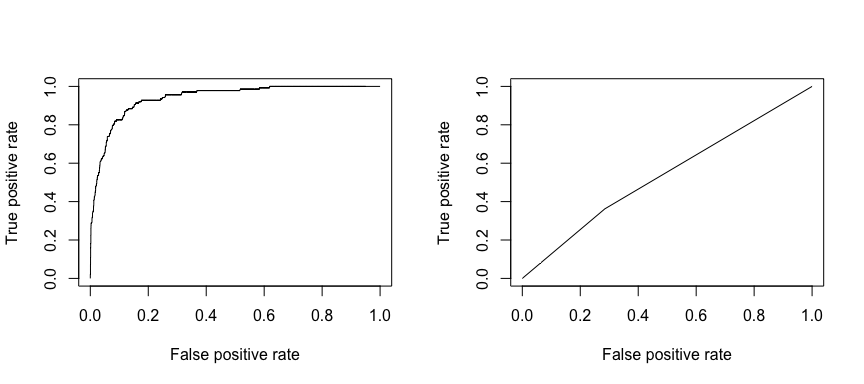

A pro numerický výpočet AUC můžeme použít následující. Nezapomeňte, že AUC se bude pohybovat v rozmezí 0,50 – 1,00. Model 2 je tedy velmi špatně klasifikující model, zatímco model 1 je velmi dobře klasifikující model.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Můžeme dále „ladit“ naše modely, abychom tyto míry klasifikace zlepšili. Pokud se vám podaří zlepšit křivky AUC a ROC (což znamená, že zlepšujete míru přesnosti klasifikace), vytváříte „lift“, což znamená, že zvedáte přesnost klasifikace.

Další zdroje

Tímto se dostanete k práci s logistickou regresí. Mějte na paměti, že je toho mnohem více, do čeho můžete proniknout, takže následující zdroje vám pomohou dozvědět se více:

• Úvod do statistického učení
• Aplikované prediktivní modelování
• Prvky statistického učení

.