'
Articles

Logistinen regressio

author
18 minutes, 52 seconds Read

Logistisen regression (eli logit-regression tai logit-mallin) kehitti tilastotieteilijä David Cox vuonna 1958, ja se on regressiomalli, jossa vastemuuttuja Y on kategorinen. Logistisen regression avulla voidaan arvioida kategorisen vastauksen todennäköisyys yhden tai useamman ennustemuuttujan (X) perusteella. Sen avulla voidaan sanoa, että ennakoivan tekijän läsnäolo lisää (tai vähentää) tietyn lopputuloksen todennäköisyyttä tietyllä prosenttimäärällä. Tässä opetusohjelmassa käsitellään tapausta, jossa Y on binäärinen eli se voi saada vain kaksi arvoa, ”0” ja ”1”, jotka edustavat sellaisia tuloksia kuin hyväksytty/hylätty, voitto/häviö, elossa/kuollut tai terve/sairas. Tapaukset, joissa riippuvaisella muuttujalla on enemmän kuin kaksi tulosluokkaa, voidaan analysoida multinomiaalisella logistisella regressiolla tai, jos useat luokat ovat järjestettyjä, ordinaalisella logistisella regressiolla. Diskriminaatioanalyysistä on kuitenkin tullut suosittu menetelmä moniluokkaiseen luokitteluun, joten seuraavassa opetusohjelmassamme keskitytään kyseiseen tekniikkaan näissä tapauksissa.

tl;dr

Tämä opetusohjelma toimii johdantona logistiseen regressioon, ja se käsittelee1:

  1. Replikointivaatimukset: Mitä tarvitset tämän opetusohjelman analyysin toistamiseen
  2. Miksi logistinen regressio: Miksi käyttää logistista regressiota?
  3. Tietojemme valmistelu: Valmistele aineistomme mallintamista varten
  4. Yksinkertainen logistinen regressio: Vastauksen Y todennäköisyyden ennustaminen yhdellä ennustemuuttujalla X
  5. Moninkertainen logistinen regressio: Vastauksen Y todennäköisyyden ennustaminen useilla ennustemuuttujilla
  6. Mallin arviointi & diagnostiikka: Kuinka hyvin malli sopii dataan? Mitkä ennustajat ovat tärkeimpiä? Ovatko ennusteet tarkkoja?

Replikointivaatimukset

Tässä opetusohjelmassa hyödynnetään ensisijaisesti Default-paketin ISLR tarjoamia tietoja. Kyseessä on simuloitu aineisto, joka sisältää tietoja kymmenestätuhannesta asiakkaasta, kuten onko asiakas maksuhäiriöinen, onko hän opiskelija, asiakkaan keskimääräinen saldo ja asiakkaan tulot. Käytämme myös muutamia paketteja, jotka tarjoavat datan käsittelyä, visualisointia, putkimallinnusfunktioita ja mallin tulosteen siistimisfunktioita. 

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Miksi logistinen regressio

Lineaarinen regressio ei sovellu laadullisen vastauksen tapauksessa. Miksi ei? Oletetaan, että yritämme ennustaa päivystyspoliklinikalla olevan potilaan terveydentilaa hänen oireidensa perusteella. Tässä yksinkertaistetussa esimerkissä on kolme mahdollista diagnoosia: aivohalvaus, huumeiden yliannostus ja epileptinen kohtaus. Voisimme harkita näiden arvojen koodaamista kvantitatiiviseksi vastemuuttujaksi, Y , seuraavasti:

Käyttäen tätä koodausta voitaisiin pienimmän neliösumman avulla sovittaa lineaarinen regressiomalli ennustamaan Y:tä joukon prediktoreiden perusteella . Valitettavasti tämä koodaus merkitsee lopputulosten järjestystä, sillä se asettaa lääkkeiden yliannostuksen aivohalvauksen ja epileptisen kohtauksen väliin ja vaatii, että aivohalvauksen ja lääkkeiden yliannostuksen välinen ero on sama kuin lääkkeiden yliannostuksen ja epileptisen kohtauksen välinen ero. Käytännössä tähän ei ole mitään erityistä syytä. Voidaan esimerkiksi valita yhtä järkevä koodaus,

, joka merkitsisi täysin erilaista suhdetta näiden kolmen tilan välillä. Kukin näistä koodauksista tuottaisi perustavanlaatuisesti erilaisia lineaarisia malleja, jotka lopulta johtaisivat erilaisiin ennusteisiin testihavainnoista.

Aineistomme kannalta olennaisempaa on se, että jos yritämme luokitella asiakkaan saldon perusteella korkean vs. matalan riskin laiminlyöjäksi, voisimme käyttää lineaarista regressiota; vasemmanpuoleinen alla oleva kuvio havainnollistaa kuitenkin sitä, miten lineaarinen regressio ennustaisi laiminlyönnin todennäköisyyttä. Valitettavasti lähellä nollaa oleville saldoille ennustamme negatiivisen maksukyvyttömyyden todennäköisyyden; jos ennustaisimme hyvin suurille saldoille, saisimme arvoja, jotka olisivat suurempia kuin 1. Nämä ennusteet eivät ole järkeviä, sillä tietysti maksukyvyttömyyden todellisen todennäköisyyden on luottokortin saldosta riippumatta oltava 0:n ja 1:n välissä.

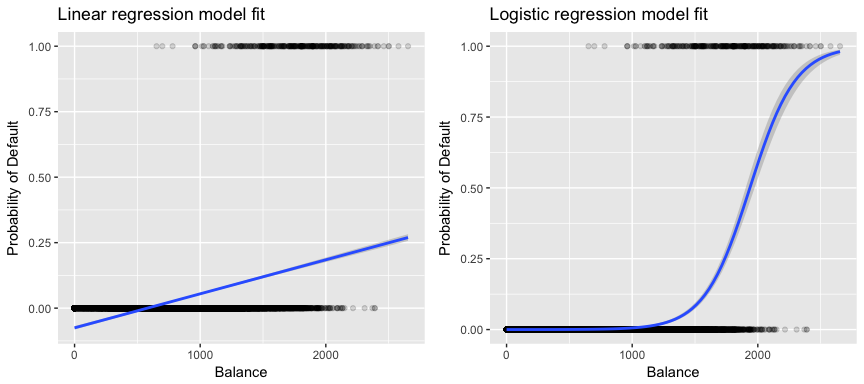
Välttääksemme tämän ongelman meidän on mallinnettava p(X) käyttämällä funktiota, joka antaa ulostulot 0:n ja 1:n väliltä kaikille X:n arvoille. Monet funktiot täyttävät tämän kuvauksen. Logistisessa regressiossa käytämme logistista funktiota, joka on määritelty yhtälössä 1 ja jota on havainnollistettu yllä olevassa oikeanpuoleisessa kuvassa.

Aineistomme valmistelu

Kuten regressio-opetuksessa, jaamme aineistomme harjoittelu- (60 %) ja testaustietoaineistoihin (40 %), jotta voimme arvioida, miten hyvin mallimme suoriutuu otoksen ulkopuolisesta aineistosta.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Yksinkertainen logistinen regressio

Sovitamme logistisen regressiomallin ennustaaksemme asiakkaan maksukyvyttömyyden todennäköisyyttä asiakkaan keskimääräisen saldon perusteella. glm-funktio sovittaa yleistettyjä lineaarisia malleja, joka on mallien luokka, johon logistinen regressio kuuluu. glm-funktion syntaksi on samanlainen kuin lm:n, paitsi että meidän on välitettävä argumentti family = binomial, jotta voimme käskeä R:ää suorittamaan logistisen regression eikä jotakin muuta yleistetyn lineaarisen mallin tyyppiä.

model1 <- glm(default ~ balance, family = "binomial", data = train)

Taustalla glm, käyttää maksimaalista todennäköisyyttä mallin sovittamiseen. Perusintuitio sille, että logistisen regressiomallin sovittamiseen käytetään maksimaalista todennäköisyyttä, on seuraava: etsitään estimaatteja arvoille ja siten, että kunkin yksilön ennustettu maksuhäiriötodennäköisyys yhtälön 1 avulla vastaa mahdollisimman hyvin yksilön havaittua maksuhäiriötilannetta. Toisin sanoen pyrimme löytämään ja siten, että näiden estimaattien liittäminen yhtälön 1 mukaiseen p(X)-malliin tuottaa luvun, joka on lähellä yhtä kaikille maksukyvyttömiksi jääneille henkilöille, ja luvun, joka on lähellä nollaa kaikille maksukyvyttömiksi jääneille henkilöille. Tämä intuitio voidaan formalisoida matemaattisella yhtälöllä, jota kutsutaan todennäköisyysfunktioksi:

Estimaatit ja valitaan siten, että maksimoidaan tämä todennäköisyysfunktio. Maximum likelihood on hyvin yleinen lähestymistapa, jota käytetään monien ei-lineaaristen mallien sovittamiseen, joita tarkastelemme tulevissa opetusohjelmissa. Tuloksena on S-muotoinen todennäköisyyskäyrä, jota on havainnollistettu alla (huomaa, että logistisen regression sovitussuoran piirtämiseksi meidän on muunnettava vastemuuttujamme binäärikoodatuksi muuttujaksi).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

Samankaltaisesti kuin lineaarisen regression kohdalla, voimme arvioida mallia käyttämällä summary tai glance. Huomaa, että kertoimen tulostusmuoto on samanlainen kuin lineaarisessa regressiossa; summary:n alareunassa olevat sovituksen hyvyyden yksityiskohdat ovat kuitenkin erilaiset. Perehdymme tähän tarkemmin myöhemmin, mutta huomaa vain, että näet sanan poikkeama. Poikkeama on analoginen lineaarisen regression neliösummalaskelmien kanssa, ja se on logistisen regressiomallin aineistoon sopimattomuuden mitta. Nollapoikkeama edustaa eroa sellaisen mallin, jossa on vain leikkauspiste (mikä tarkoittaa ”ei ennusteita”), ja tyydytetyn mallin (malli, jossa on teoreettisesti täydellinen sovitus) välillä. Tavoitteena on, että mallin poikkeama (jota kutsutaan jäännöspoikkeamaksi) on pienempi; pienemmät arvot osoittavat parempaa sopivuutta. Tältä osin nollamalli tarjoaa lähtötason, johon verrata ennustemalleja.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

Kertoimien arviointi

Alla olevassa taulukossa esitetään kertoimien estimaatit ja niihin liittyvät tiedot, jotka saadaan sovittamalla logistinen regressiomalli ennustamaan maksulaiminlyönnin todennäköisyyttä = Kyllä saldoa käyttäen. Muista, että logistisesta regressiosta saadut kerroinestimaatit kuvaavat ennustemuuttujan ja vastemuuttujan välistä suhdetta logaritmisella asteikolla (katso lisätietoja ISLR1:n luvusta 3). Näin ollen näemme, että ; tämä osoittaa, että saldon kasvu liittyy maksulaiminlyönnin todennäköisyyden kasvuun. Tarkemmin sanottuna yhden yksikön suuruinen saldon lisäys liittyy maksuhäiriön log-kertoimen kasvuun 0,0057 yksiköllä.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Voimme tulkita saldokertoimen edelleen seuraavasti – jokaista dollarin suuruista kuukausittaisen saldon lisäystä kohti asiakkaan maksuhäiriön todennäköisyys kasvaa kertoimella 1.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

Monet kertoimen tuloksen näkökohdat ovat samanlaisia kuin lineaarisen regression tuloksessa käsitellyt näkökohdat. Voimme esimerkiksi mitata kerroinestimaattien luottamusvälejä ja tarkkuutta laskemalla niiden keskivirheet. Esimerkiksi p-arvo < 2e-16 viittaa tilastollisesti merkitsevään suhteeseen taseen ja maksukyvyttömyyden todennäköisyyden välillä. Voimme myös käyttää keskivirheitä luottamusvälien saamiseksi, kuten teimme lineaarisen regression opetusohjelmassa:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Ennusteiden tekeminen

Kun kertoimet on estimoitu, on yksinkertaista laskea maksulaiminlyönnin todennäköisyys mille tahansa luottokorttisaldolle. Matemaattisesti käyttämällä mallimme kerroinestimaatteja ennustamme, että maksulaiminlyönnin todennäköisyys henkilöllä, jolla on 1000 dollarin saldo, on alle 0,5 %

Voimme ennustaa maksulaiminlyönnin todennäköisyyden R:ssä käyttämällä predict-funktiota (muista sisällyttää type = "response"). Tässä vertaamme maksuhäiriön todennäköisyyttä 1000 ja 2000 dollarin saldojen perusteella. Kuten näet, kun saldo siirtyy 1000 dollarista 2000 dollariin, maksukyvyttömyyden todennäköisyys kasvaa huomattavasti, 0,5 prosentista 58 prosenttiin!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

Logistisen regressiomallin kanssa voidaan käyttää myös laadullisia ennusteita. Esimerkkinä voidaan sovittaa malli, jossa käytetään muuttujaa student.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

Muuttujaan student = Yes liittyvä kerroin on positiivinen, ja siihen liittyvä p-arvo on tilastollisesti merkitsevä. Tämä osoittaa, että opiskelijoilla on yleensä korkeampi maksuhäiriötodennäköisyys kuin ei-opiskelijoilla. Itse asiassa tämä malli viittaa siihen, että opiskelijalla on lähes kaksinkertainen todennäköisyys joutua maksukyvyttömäksi kuin ei-opiskelijoilla. Seuraavassa jaksossa näemme kuitenkin, miksi.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Moninkertainen logistinen regressio

Voidaan myös laajentaa malliamme yhtälön mukaisesti. 1 siten, että voimme ennustaa binäärisen vastauksen käyttämällä useita ennustajia, joissa on p ennustajia:

Sovitetaan nyt malli, joka ennustaa maksuhäiriön todennäköisyyttä saldo-, tulo- (tuhansina dollareina) ja opiskelijan asemaa kuvaavien muuttujien perusteella. Tässä on yllättävä tulos. Saldoon ja opiskelija=Kyllä-statukseen liittyvät p-arvot ovat hyvin pieniä, mikä osoittaa, että kukin näistä muuttujista on yhteydessä maksuhäiriön todennäköisyyteen. Opiskelija-muuttujan kerroin on kuitenkin negatiivinen, mikä osoittaa, että opiskelijat laiminlyövät maksujaan pienemmällä todennäköisyydellä kuin muut kuin opiskelijat. Sitä vastoin opiskelijamuuttujan kerroin mallissa 2, jossa ennustettiin maksulaiminlyönnin todennäköisyyttä vain opiskelijan aseman perusteella, osoitti, että opiskelijoiden maksulaiminlyönnin todennäköisyys on suurempi. Mistä se johtuu?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Alla olevan kuvion oikeanpuoleisessa paneelissa on selitys tälle ristiriidalle. Muuttujat opiskelija ja saldo korreloivat keskenään. Opiskelijoilla on yleensä enemmän velkaa, mikä puolestaan liittyy suurempaan maksuhäiriöiden todennäköisyyteen. Toisin sanoen opiskelijoilla on todennäköisemmin suuria luottokorttisaldoja, jotka, kuten alla olevan kuvion vasemmanpuoleisesta paneelista tiedetään, ovat yleensä yhteydessä korkeisiin maksuhäiriöasteisiin. Vaikka yksittäisellä opiskelijalla, jolla on tietty luottokorttisaldo, on yleensä pienempi maksuhäiriötodennäköisyys kuin ei-opiskelijalla, jolla on sama luottokorttisaldo, se, että opiskelijoilla on yleisesti ottaen suuremmat luottokorttisaldot, tarkoittaa sitä, että opiskelijat laiminlyövät maksujaan yleisesti ottaen useammin kuin ei-opiskelijat. Tämä on tärkeä ero luottokorttiyhtiölle, joka yrittää määrittää, kenelle sen pitäisi tarjota luottoa. Opiskelija on riskialttiimpi kuin ei-opiskelija, jos opiskelijan luottokorttisaldosta ei ole saatavilla tietoja. Opiskelija on kuitenkin vähemmän riskialtis kuin ei-opiskelija, jolla on sama luottokorttisaldo!

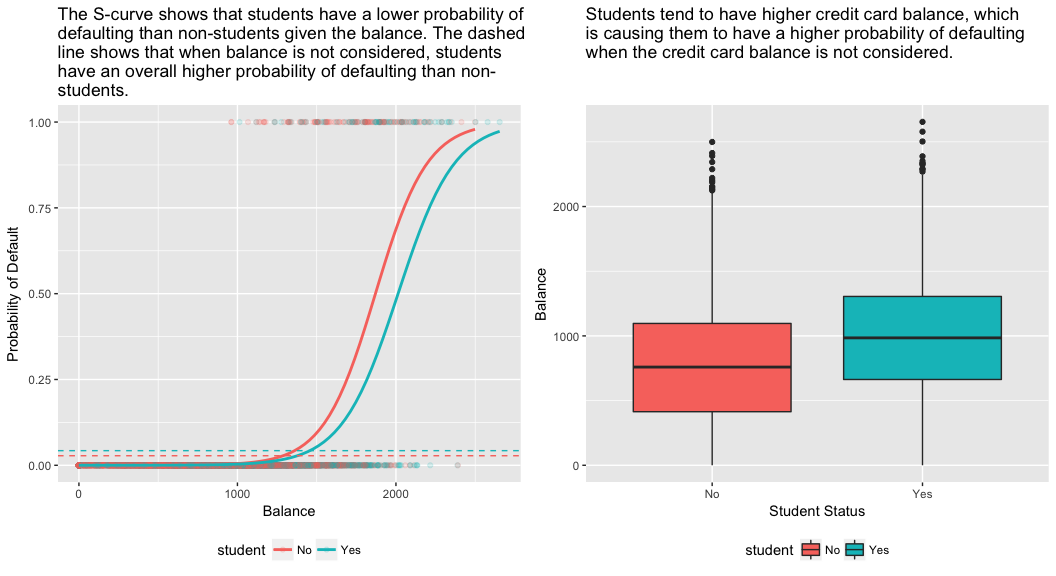
Tämä yksinkertainen esimerkki havainnollistaa vaaroja ja hienovaraisuuksia, jotka liittyvät regressioiden tekemiseen, joissa on mukana vain yksi ennustava tekijä, kun myös muut ennustavat tekijät voivat olla merkityksellisiä. Yhden ennustajan avulla saadut tulokset voivat olla aivan erilaisia kuin useamman ennustajan avulla saadut tulokset, varsinkin jos ennustajien välillä on korrelaatiota. Tämä ilmiö tunnetaan nimellä confounding.

Monien ennustemuuttujien tapauksessa halutaan joskus ymmärtää, mikä muuttuja vaikuttaa eniten vastemuuttujan (Y) ennustamiseen. Voimme tehdä tämän caret-paketin varImp avulla. Tässä näemme, että tasapaino on ylivoimaisesti tärkein, kun taas opiskelijan asema on vähemmän tärkeä, ja sen jälkeen tulevat tulot (jotka osoittautuivat joka tapauksessa merkityksettömiksi (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Kuten aiemminkin, voimme helposti tehdä ennusteita tämän mallin avulla. Esimerkiksi opiskelijalla, jolla on 1500 dollarin luottokorttisaldo ja 40 000 dollarin tulot, on arvioitu maksuhäiriötodennäköisyys

Eiopiskelijalla, jolla on sama saldo ja samat tulot, on arvioitu maksuhäiriötodennäköisyys

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Näimme siis, että annetulla saldolla ja tuloilla (vaikka tulot ovatkin merkityksetön tekijä) opiskelijan maksuhäiriötodennäköisyys on suurin piirtein puolet alhaisempi kuin ei-opiskelijan.

Mallien arviointi & Diagnostiikka

Tähän mennessä on rakennettu kolme logistista regressiomallia ja tarkasteltu niiden kertoimia. Joitakin kriittisiä kysymyksiä on kuitenkin vielä jäljellä. Ovatko mallit yhtään hyviä? Kuinka hyvin malli sopii aineistoon? Ja kuinka tarkkoja ennusteet ovat otoksen ulkopuolisella aineistolla?

Goodness-of-Fit

Lineaarisen regression opetusohjelmassa näimme, kuinka F-statistiikka ja oikaistu , ja jäännösdiagnostiikka kertovat meille, kuinka hyvin malli sopii aineistoon. Tässä tarkastelemme muutamia tapoja arvioida logit-mallimme sopivuuden hyvyyttä.

Likelihood Ratio Test

Ensin voimme käyttää Likelihood Ratio Testiä arvioidaksemme, parantavatko mallimme sopivuutta. Ennustemuuttujien lisääminen malliin parantaa lähes aina mallin sopivuutta (eli kasvattaa log likelihoodia ja pienentää mallipoikkeamaa nollapoikkeamaan verrattuna), mutta on tarpeen testata, onko havaittu ero mallin sopivuudessa tilastollisesti merkitsevä. Voimme käyttää anova tämän testin suorittamiseen. Tulokset osoittavat, että verrattuna model1:aan model3 vähentää jäännöspoikkeamaa yli 13:lla (muistakaa, että logistisen regression tavoitteena on löytää malli, joka minimoi poikkeaman jäännökset). Vielä tärkeämpää on, että tämä parannus on tilastollisesti merkitsevä (p = 0,001). Tämä viittaa siihen, että model3 parantaa mallin sopivuutta.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pseudo

Toisin kuin lineaarisessa regressiossa tavallisella pienimmän neliösumman estimoinnilla, ei ole tilastoa, joka selittäisi, kuinka suuri osa riippuvan muuttujan varianssista selittyy ennustajilla. On kuitenkin olemassa useita pseudomittareita, joista voi olla hyötyä. Merkittävin on McFaddenin arvo, joka määritellään seuraavasti:

jossa on sovitetun mallin log likelihood-arvo ja on nollamallin log likelihood-arvo, jossa ennustajana on vain leikkaus. Mittari vaihtelee 0:sta hieman alle 1:een, ja arvot lähempänä nollaa osoittavat, että mallilla ei ole ennustusvoimaa. Toisin kuin lineaarisessa regressiossa, mallit saavuttavat kuitenkin harvoin korkean McFaddenin arvon. Itse asiassa McFaddenin omien sanojen mukaan mallit, joiden McFaddenin pseudo edustavat erittäin hyvää sopivuutta. Voimme arvioida McFaddenin pseudoarvoja malleillemme seuraavasti: 

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Näemme, että mallin 2 arvo on hyvin alhainen, mikä vahvistaa sen huonon sopivuuden. Mallien 1 ja 3 arvot ovat kuitenkin paljon korkeammat, mikä viittaa siihen, että ne selittävät kohtuullisen määrän oletusaineiston varianssista. Lisäksi näemme, että malli 3 parantaa arvoa vain hieman.

Jäännösarviointi

Muista, että logistisessa regressiossa ei oleteta, että jäännökset ovat normaalisti jakautuneita tai että varianssi on vakio. Poikkeusjäännös on kuitenkin hyödyllinen määritettäessä, jos yksittäiset pisteet eivät sovi malliin hyvin. Tässä voimme sovittaa standardoidut poikkeamajäännökset nähdaksemme, kuinka moni niistä ylittää 3 standardipoikkeamaa. Ensin poimimme useita hyödyllisiä pätkiä mallin tuloksista augment:llä ja siirrymme sitten piirtämään. 

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)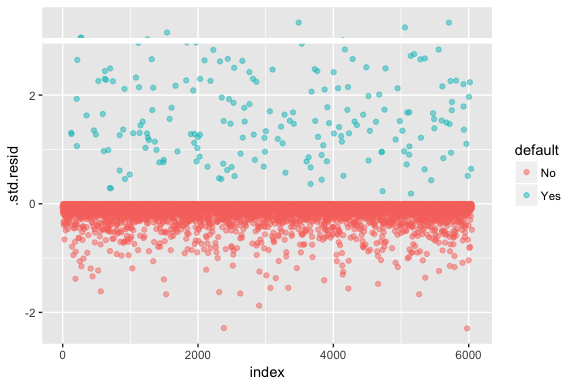

Ne standardoidut jäännökset, jotka ylittävät 3, edustavat mahdollisia poikkeamia ja saattavat ansaita tarkempaa huomiota. Voimme suodattaa nämä residuaalit tarkempaa tarkastelua varten. Näemme, että kaikki nämä havainnot edustavat asiakkaita, jotka laiminlöivät maksujaan budjeteilla, jotka ovat paljon pienempiä kuin normaalit laiminlyöjät.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

Lineaarisen regression tapaan voimme myös tunnistaa vaikutusvaltaiset havainnot Cookin etäisyysarvojen avulla. Tässä tunnistamme 5 suurinta arvoa.

plot(model1, which = 4, id.n = 5)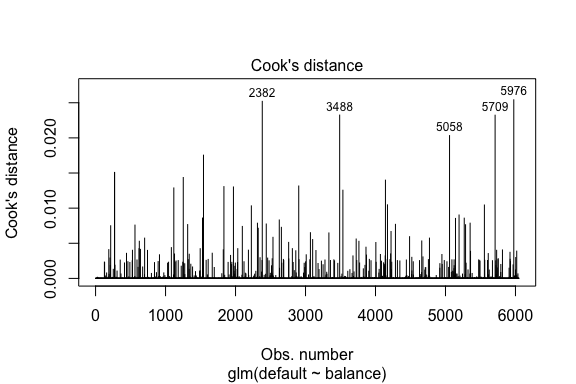

Ja näitäkin voimme tutkia tarkemmin. Tässä näemme, että viisi suurinta vaikuttavaa pistettä sisältävät:

  • ne asiakkaat, jotka laiminlöivät maksunsa hyvin pienillä saldoilla, ja
  • kaksi asiakasta, jotka eivät laiminlyöneet maksujaan, mutta joiden saldot olivat kuitenkin yli 2 000 dollaria

Tämä tarkoittaa, että jos poistaisimme nämä havainnot (ei suositella), logistisen regressiomme S-käyrän muoto, sijaintikohta ja luotettavuusvyöhyke muuttuisivat todennäköisesti.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

Ennustettujen arvojen validointi

Luokitusaste

Kehitettäessä malleja ennustamista varten kriittisin mittari koskee sitä, miten hyvin malli ennustaa kohdemuuttujaa otoksen ulkopuolisilla havainnoilla. Ensin meidän on käytettävä estimoituja malleja ennustamaan arvoja harjoitusaineistossamme (train). Kun käytät predict, muista sisällyttää type = response, jotta ennuste palauttaa oletusarvon todennäköisyyden. 

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Nyt voimme verrata ennustettua kohdemuuttujaa ja havaittuja arvoja kunkin mallin osalta ja katsoa, mikä niistä suoriutuu parhaiten. Voimme aloittaa käyttämällä sekoitusmatriisia, joka on taulukko, joka kuvaa kunkin mallin luokittelusuoritusta testiaineistossa. Taulukon jokaisella kvadrantilla on tärkeä merkitys. Tässä tapauksessa riveillä olevat ”Ei” ja ”Kyllä” tarkoittavat sitä, ovatko asiakkaat laiminlyöneet maksuja vai eivät. ”FALSE” ja ”TRUE” sarakkeissa edustavat sitä, ennustimmeko, että asiakkaat laiminlyövät maksun vai eivät.

  • tosi positiiviset (oikeanpuoleinen alakulmankvadrantti): Nämä ovat tapauksia, joissa ennustimme asiakkaan laiminlyövän maksun ja hän laiminlöi maksun.
  • tosi negatiiviset (vasemmanpuoleinen yläkulmankvadrantti): Ennustimme, ettei maksukyvyttömyyttä ole, ja asiakas ei maksukyvyttömäksi jäänyt.
  • vääriä positiivisia tapauksia (oikeanpuoleinen yläkvadrantti): Ennustimme kyllä, mutta asiakas ei todellisuudessa laiminlyönyt maksujaan. (Tunnetaan myös nimellä ”tyypin I virhe”.)
  • vääriä negatiivisia (alhaalla vasemmalla): Ennustimme ei, mutta he tekivätkin maksuhäiriöitä. (Tunnetaan myös nimellä ”tyypin II virhe.”)

Tulokset osoittavat, että model1 ja model3 ovat hyvin samanlaisia. 96 % ennustetuista havainnoista on todellisia negatiivisia ja noin 1 % todellisia positiivisia. Molempien mallien tyypin II virhe on alle 3 %, jolloin malli ennustaa, että asiakas ei laiminlyö, mutta hän tosiasiassa laiminlöi. Molempien mallien I-tyyppivirhe on alle 1 %, kun malli ennustaa, että asiakas joutuu maksukyvyttömäksi, mutta hän ei koskaan joutunut maksukyvyttömäksi. model2 Tulokset ovat huomattavan erilaiset; tämä malli ennustaa tarkasti ne asiakkaat, jotka eivät ole maksukyvyttömiä (mikä johtuu siitä, että 97 % aineistosta on maksukyvyttömiä), mutta ei koskaan ennusta niitä asiakkaita, jotka maksukyvyttömiksi jäävät!

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

Haluamme myös ymmärtää luokitteluvirheiden (eli virheiden) prosenttiosuudet (tai voisimme kääntää tämän tarkkuusprosentiksi). Emme näe suurta parannusta mallien 1 ja 3 välillä, ja vaikka mallin 2 virheprosentti on alhainen, älä unohda, että se ei koskaan ennusta tarkasti asiakkaita, jotka todella laiminlyövät maksujaan. 

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

Voitamme saada lisäymmärrystä tarkastelemalla sekaannusmatriisin raakamääräisiä arvoja (ei prosentteja). Tarkastellaan mallia 1 havainnollistamiseksi. Näemme, että maksuhäiriöisiä asiakkaita on yhteensä kappaletta. Kaikista laiminlyönneistä ei ennustettu. Vaihtoehtoisesti voisimme sanoa, että vain osa maksuhäiriöistä ennustettiin – tämä tunnetaan mallin tarkkuutena (tai herkkyytenä). Vaikka kokonaisvirheprosentti on siis alhainen, myös tarkkuusprosentti on alhainen, mikä ei ole hyvä!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Luokittelumallien yhteydessä käytetään myös termejä herkkyys (sensititivy) ja spesifisyys (specificity), kun kuvaillaan mallin suorituskykyä. Kuten edellä mainittiin, herkkyys on synonyymi tarkkuudelle. Spesifisyys on kuitenkin se prosenttiosuus oikein tunnistetuista ei-laiminlyöjistä, tässä (tässä tarkkuus johtuu pitkälti siitä, että 97 % aineistomme havainnoista on ei-laiminlyöjiä). Herkkyyden ja spesifisyyden välinen merkitys riippuu asiayhteydestä. Tässä tapauksessa luottokorttiyhtiö on todennäköisesti enemmän huolissaan herkkyydestä, koska se haluaa vähentää riskiä. Siksi se saattaa olla enemmän huolissaan mallin virittämisestä niin, että sen herkkyys/tarkkuus paranee.

Vastaanottava toimintaominaisuus (ROC, receiving operating characteristic) on luokittelijan suorituskyvyn visuaalinen mittari. Käyttämällä oikein positiivisiksi katsottujen positiivisten datapisteiden osuutta ja virheellisesti positiivisiksi katsottujen negatiivisten datapisteiden osuutta luodaan graafinen kuvaaja, joka näyttää vaihtosuhteen oikein ennustamisen nopeuden ja virheellisesti ennustamisen nopeuden välillä. Viime kädessä olemme huolissamme ROC-käyrän alaisesta pinta-alasta eli AUC:stä. Tämä mittari vaihtelee välillä 0,50-1,00, ja arvot yli 0,80 osoittavat, että malli tekee hyvää työtä erottaessaan kohdemuuttujamme muodostavat kaksi luokkaa toisistaan. Voimme verrata ROC- ja AUC-arvoja mallien 1 ja 2 osalta, joiden suorituskyvyssä on suuri ero. Haluamme ehdottomasti, että ROC-käyrästömme näyttävät enemmän mallin 1 (vasemmalla) kuin mallin 2 (oikealla) kaltaisilta!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()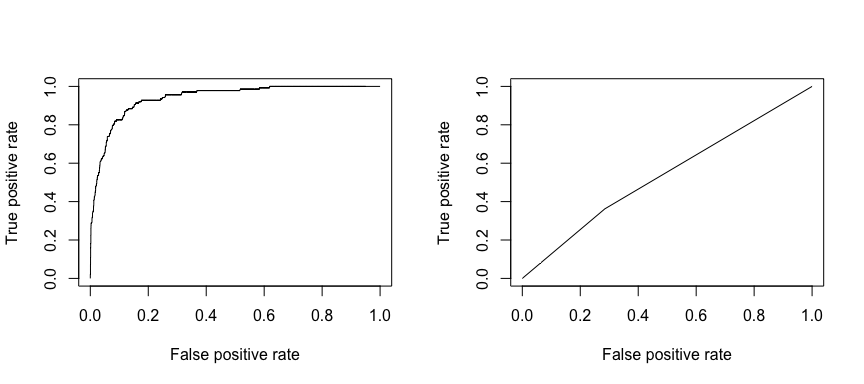

Ja voidaksemme laskea AUC:n numeerisesti voimme käyttää seuraavaa. Muista, että AUC vaihtelee välillä .50 – 1.00. Malli 2 on siis erittäin huono luokitteleva malli, kun taas malli 1 on erittäin hyvä luokitteleva malli.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

Voidaan jatkaa mallien ”virittämistä” näiden luokitusasteiden parantamiseksi. Jos pystyt parantamaan AUC- ja ROC-käyriäsi (mikä tarkoittaa, että parannat luokittelutarkkuusprosentteja), luot ”nostetta” eli nostat luokittelutarkkuutta.

Lisäresurssit

Tämän avulla pääset alkuun logistisen regression kanssa. Pidä mielessä, että on paljon muutakin, mihin voit syventyä, joten seuraavat resurssit auttavat sinua oppimaan lisää:

  • An Introduction to Statistical Learning
  • Applied Predictive Modeling
  • Elements of Statistical Learning

  2. Tämä opetusohjelma on laadittu An Introduction to Statistical Learning 2

-kirjan luvun 4 jakson 3 täydentämiseksi.

Similar Posts

Vastaa

Sähköpostiosoitettasi ei julkaista.