Poločas

Obrázek 1. Graf znázorňující rozpad radioaktivního jádra v čase. Doba, za kterou hmotnost nebo aktivita zdroje (počet rozpadů za sekundu) klesne na 50 %, je poločas rozpadu. Poločas rozpadu na tomto obrázku je 1 rok.

Poloviční život je doba, za kterou se rozpadne polovina původní hodnoty určitého množství radioaktivního prvku. Kromě toho je jeden poločas rozpadu doba, za kterou klesne aktivita zdroje na polovinu původní hodnoty. Druhý termodynamický zákon, konkrétně větu o neuspořádanosti, lze použít k pochopení toho, proč dochází k radioaktivnímu rozpadu. Toto tvrzení říká, že entropie uzavřeného systému nemůže nikdy klesat, což znamená, že věci musí dále upadat do neuspořádanosti, nikoliv do řádu. Tento proces je znám jako „rozpad“ a druhý zákon pomáhá objasnit, proč se hmota časem rozpadá do stále méně uspořádaného stavu tento . Součástí tohoto procesu jsou určité typy atomů, které se rozpadají na nové, odlišné typy atomů určitou měřitelnou rychlostí známou jako radioaktivní rozpad.

Všechny radioaktivní materiály mají v sobě nestabilní jádra. Kromě toho jsou v látce také některá jádra, která jsou již ve stabilním stavu, ale poměr stabilních a nestabilních jader ve vzorku se může lišit. Stabilní jádra ve vzorku jsou neměnná (a ve stabilním energetickém stavu), ale nestabilní jádra časem projdou nějakým druhem jaderného rozpadu a stanou se stabilními. Výsledkem je emise určité formy záření. Protože poločas rozpadu je měřítkem času, je poločas rozpadu hodnotou, která určuje, jak dlouho bude tento přechod do stabilnějšího energetického stavu trvat.

Různé látky zaznamenávají ztrátu své radioaktivity rychleji než jiné. U některých radioaktivních prvků může dojít k rozpadu poloviny jejich nestabilních jader za méně než jednu sekundu. Například krypton-101 má poločas rozpadu přibližně deset miliontin sekundy. Naproti tomu některé prvky mají mimořádně dlouhý poločas rozpadu a jejich rozpad trvá miliardy let. Uran-238 má poločas rozpadu 4,51 miliardy let. To znamená, že rozpad uranu-238 na poměr poloviny uranu-238 a poloviny thoria-234 by trval miliardy let. Uran-235 (další přirozeně se vyskytující izotop uranu) má kratší poločas rozpadu než uran-238, tedy pouze ~700 milionů let.

Rovnice

Existuje rovnice, která se často používá k určení, kolik určité radioaktivní látky zůstane po uplynutí dané doby. To se určuje na základě vlastností, jako je poločas rozpadu látky, a toho, kolik látky bylo na počátku. Používá se rovnice:

kde:

• je množství látky po uplynutí času
• je počáteční množství látky
• je doba, která uplynula
• je poločas rozpadu látky

Dále lze podobnou rovnici použít k zobrazení toho, jak se aktivita látky v průběhu času snižuje. Při tomto vyjádření má rovnice tvar:

kde:

• je aktivita látky po uplynutí času
• je počáteční aktivita látky
• je doba, která uplynula
• je poločas rozpadu látky

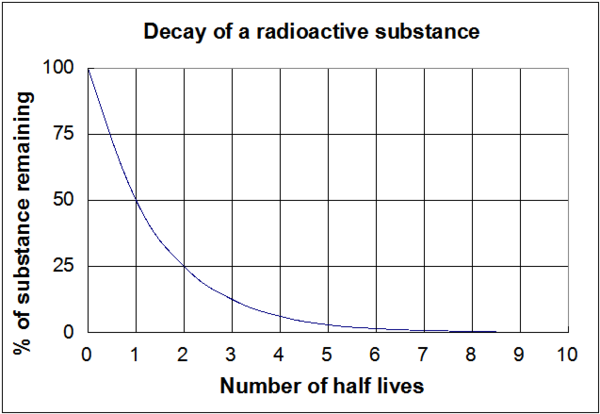
Graf zobrazený na obrázku 1 je vizuálním znázorněním těchto výše uvedených rovnic. Je důležité si uvědomit, že bez ohledu na skutečnou délku poločasu rozpadu (ať už jde o miliony let nebo několik nanosekund) bude tvar grafu stejný.

Znalost poločasů rozpadu je součástí způsobu, jakým geologové datují horniny pomocí radioizotopového datování.

.