V dnešním příspěvku se dozvíte, jaký je rozdíl mezi prvočísly a složenými čísly. Navíc si ukážeme několik příkladů, které vám je pomohou lépe pochopit.
Index
Co jsou to prvočísla?
Prvočísla jsou čísla, která jsou dělitelná pouze sama sebou a jedničkou, jinými slovy, pokud se je pokusíme vydělit jiným číslem, výsledek není celé číslo. Pokud tedy číslo vydělíme něčím jiným než jedničkou nebo sebou samým, dostaneme zbytek, který není nula.
Prvočísla do 100
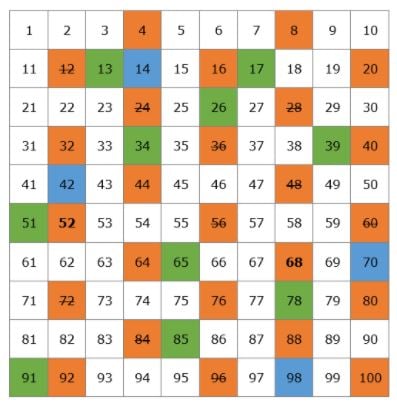
Vytvoříme si tabulku se všemi prvočísly, která existují do 100.
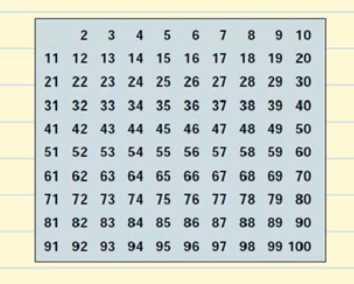
Začneme číslem 2.
Je to číslo, které je dělitelné jedničkou. 2 je prvočíslo, ale všechny násobky 2 budou složená čísla, protože budou dělitelné číslem 2. V tabulce vyškrtneme všechny násobky 2.
Další prvočíslo je 3, takže můžeme vyškrtnout všechny násobky 3, protože budou složená čísla.
Po 3 je další prvočíslo 5, takže vyškrtneme všechny násobky 5.
Poté máme prvočíslo 7 a vyškrtneme všechny násobky 7.
Další prvočíslo je 11, takže vyškrtneme všechny násobky 11, kterými jsou 22, 33, 44, 55, 66, 77, 88 a 99.
Další prvočíslo je 11, takže vyškrtneme všechny násobky 11, které jsou na tabulce. Všechna tato čísla jsme již vyškrtli, takže jsme dokončili vyškrtávání všech složených čísel v naší tabulce.

Tímto je náš seznam prvočísel od 1 do 100. Nemusíte se je učit nazpaměť, ale nejlepší by bylo, kdybyste si zapamatovali menší čísla, například 2, 3, 5, 7, 11, 13.
Kolik je prvočísel?
Řecký matematik Eratosthenes (3. stol. př. n. l.) navrhl rychlý způsob, jak najít všechna prvočísla až po libovolné číslo. Tento postup se nazývá Eratosthenovo síto.
Všimněte si, že mezi 1 a 100 je 25 prvočísel. Kolik je celkem prvočísel? Už od starověku víme, že jich je nekonečně mnoho, takže není možné vyjmenovat všechna. Protože Euklides, který ve 4. století př. n. l. jako první ukázal, že jich je nekonečné množství, neznal pojem nekonečna, řekl, že „prvočísel je více než jakákoli jejich pevná množina“, což znamená, že když si představíte 100, je jich více, a když si představíte milion, je jich ještě více.
Prvočísla od 100 do 1000
Podívejme se na prvočísla od 100 do 1000.

Mrzí nás, že si nemůžeme ukázat všechna, jak víte, je jich nekonečně mnoho. 😉
Prvočísla Příklady
Abychom vám pomohli lépe pochopit prvočísla, vysvětlíme si cvičení.
Sara má 6 bonbonů, o které se chce rozdělit, ale neví, s kolika lidmi se o ně může rozdělit, aby všichni dostali stejné množství a žádný nezbyl. Kolika způsoby to může udělat?“
Tady je Sára a jejích 6 kousků bonbonů:

Jak je můžeme rozdělit?“
První a nejjednodušší způsob je dát je jedné osobě, jinými slovy, vydělit je číslem 1. Tak bude mít tato osoba 6 kousků bonbonů.
Další možností je rozdělit je mezi 2 osoby. Protože 6 děleno 2 je 3, každá osoba dostane 3 kusy bonbonů!“

Pokračujeme dalším číslem, 3. Pokud rozdělíme 6 kusů bonbonů mezi 3 osoby, je to také přesné dělení a každá osoba dostane 2 kusy bonbonů:

Pokračujme s čísly. U 4 a 5 přesné dělení nemáme, ale u 6 ano.
Protože 6 děleno 6 je 1, můžeme dát 6 dětem po 1 bonbonu.

Zjistíme nějaké informace. Máme 6 kusů bonbonů, které můžeme rozdělit (s přesným dělením) mezi 1, 2, 3 a 6 osob. Jinými slovy, číslo 6 můžeme vydělit a při dělení 1, 2, 3 a 6 dostaneme 0 jako zbytek. Tato čísla se nazývají dělitelé čísla 6.
Zkusíme to s jiným číslem, například s číslem 7.
Sára má nyní 7 bonbonů a chce se o ně rozdělit, ale neví, s kolika lidmi se může rozdělit, aby všichni dostali stejné množství a žádný nezbyl. Kolika způsoby to může udělat?“

Henry má takové štěstí! Dostal všechny kousky bonbónů!“
Jsou i jiné způsoby, jak to udělat? 7 nemůžeme dělit 2, 3, 4, 5 ani 6, …ale 7 je možné!“
Sara může rozdělit kousky bonbónů mezi 7 lidí, každému dá jeden kousek:

Takže 7 lze dělit pouze 1 a 7, jejími jedinými děliteli jsou 1 a 7.
Takže 7 je možné dělit pouze 1 a 7. Těmto typům čísel říkáme prvočísla.
Existuje více prvočísel? Samozřejmě! Pojďme hledat další:
- Je 4? Ne! Protože jeho děliteli jsou 1, 2 a 4.
- Je 5? Ano! Protože jeho děliteli jsou 1 a 5.
- Je 8? Ne! Protože jeho dělitelé jsou 1, 2, 4 a 8.
Zkrátka číslo je prvočíslo, pokud má pouze 2 dělitele:
Nyní můžete hledat spoustu prvočísel!
Jak najít prvočísla
Dávejte dobrý pozor! Prozradíme vám trik, jak zjistit, zda je číslo prvočíslo, nebo ne, aniž bychom museli hledat jeho dělitele, ale způsobem, který je zábavnější a který nám dělitele prozradí (pokud je má).
Zvolíme si náhodně číslo, například 16.
K tomu, abychom zjistili, zda je to prvočíslo, nebo ne, použijeme tabulku, která je velmi podobná Montessoriho kartám na násobení. A dostaneme tolik kuliček, kolik je námi zvolené číslo. V tomto případě 16 kuliček.
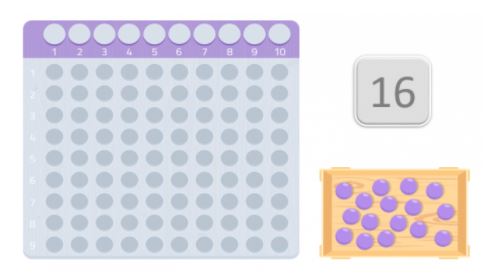
Jakmile máme tabulku a kuličky, měli bychom je položit na stůl počínaje prvním místem a snažit se vytvořit obdélník. Čísla, která tvoří okraje obdélníku, jsou děliteli tohoto čísla.
V případě, že se nám podaří vytvořit obdélník pouze se stejným číslem, které používáme, a číslem 1, bude to prvočíslo.
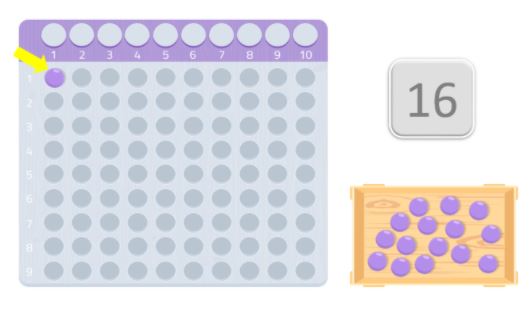
V tomto případě například umístíme 8 kuliček do první řady a dalších 8 do druhé. Jak vidíte, vytvořili jsme obdélník a vidíme, že 8, stejně jako 2, jsou děliteli čísla 16. V tomto případě se jedná o dělitele čísla 16. Proto 16 není prvočíslo, protože, jak víte, prvočísla jsou taková, která jsou dělitelná pouze sama sebou a 1.
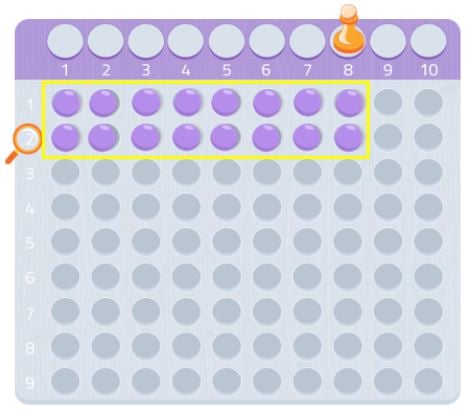
Můžeme to zkusit s jiným číslem, například se sedmičkou.
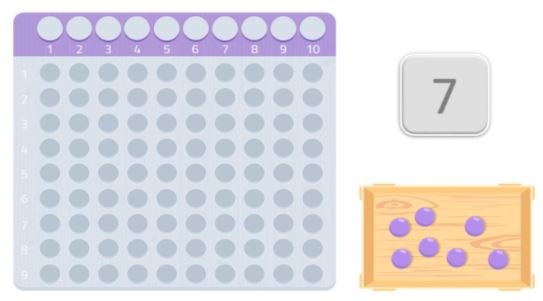
Jak vidíme, nemohli bychom vytvořit úplný obdélník, chyběla by nám kulička. Protože nejsme schopni vytvořit obdélník, mohli bychom říci, že číslo 7 nemá žádné jiné dělitele než sebe sama a 1, jak vidíme na následujícím obrázku.
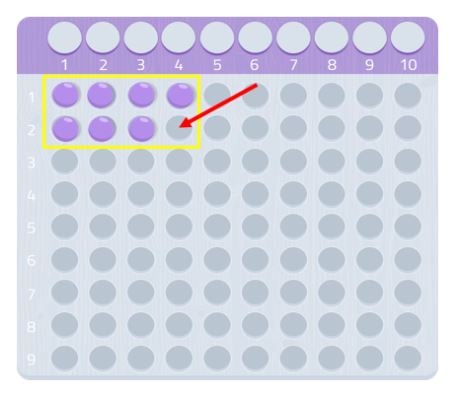
Takže 7 je prvočíslo!
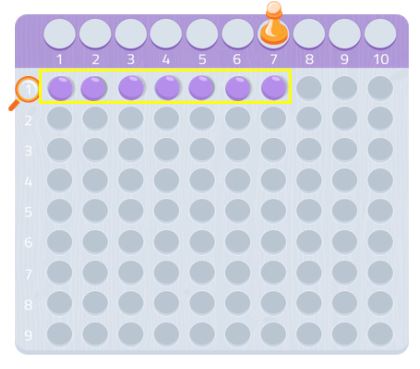
Zkuste to s jakýmkoli jiným číslem, uvidíte, jak to funguje! Můžeš použít grafický papír a hledat obdélníky pomocí tohoto počtu čtverců.
Proč jsou prvočísla důležitá?
Prvočísla jsou klíčem k aritmetice, níže uvidíte příklad, který ukazuje jejich význam nejen v matematice, ale i v přírodě.
Co máme na mysli, když říkáme, že prvočísla jsou klíčem k aritmetice?
Je to proto, že každé číslo se skládá z jedinečného součinu tvořeného řadou těchto čísel.
Předpokládá se, že se studují již asi 20 000 let, kdy si náš předek zapsal řadu prvočísel (11, 13, 17 a 19) na kost Ishango. Jako by to byla náhoda, bylo potvrzeno, že s nimi pracovali už staří Egypťané před 4 000 lety.
Příroda je navíc velmi dobře zná a některé druhy je během svého vývoje dokázaly objevit a využít k přežití.
Mám na mysli několik druhů cikád, například Magicicada septendecium, která žije v Severní Americe. Tento druh cikády si stanovil svůj rozmnožovací cyklus kolem 13 nebo 17 let, nikoliv 12, 14, 15, 16 nebo 18 – přesně 13 nebo 17 let. To jim umožňuje vyhnout se predátorům, kteří mají také periodické reprodukční cykly; představte si predátora se čtyřletým reprodukčním cyklem.
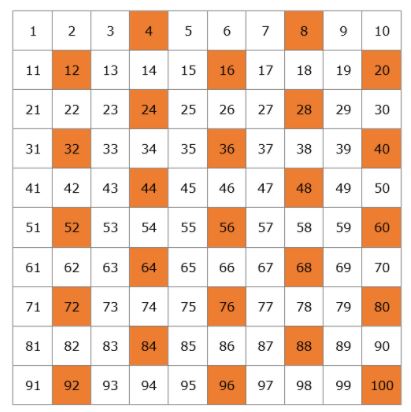
Pokud by byl životní cyklus cikády 12 nebo 14 let, shodoval by se s predátorem velmi často, mnohem častěji, než kdyby byl 13 nebo 17 let. Přesně 2krát za 100 let, zatímco jinak by se shodovaly v 11 cyklech, což by ohrozilo vývoj druhu.
Na prvočíslech je založena i bezpečnost elektronické komunikace. Každá šifrovaná zpráva odeslaná přes internet (sítě zpráv, nákupy nebo elektronické bankovnictví) má přiřazené velké číslo a je velmi obtížné zjistit, kde je prvočíslo a kde ne. Příjemce má jeden z jeho dělitelů, a proto ji může dešifrovat. Mít prvočísla je tedy pro naše soukromí při elektronické komunikaci velmi důležité.
Co jsou to složená čísla?
Složená čísla jsou taková čísla, která jsou dělitelná 1 a sebou samými i jinými čísly.
Podíváme se na příklad prvočísla a složeného čísla.
11 lze zapsat jako násobek 1 x 11, ale nelze ho zapsat jako žádný jiný násobek přirozených čísel. Má pouze dělitele 1 a 11, a proto je to prvočíslo.
12 lze zapsat jako násobení 1 x 12 a jako násobení 3 x 4 a 2 x 6. Protože 12 je dělitelné více čísly než 1 a sebou samým, je 12 složené číslo.
Je 1 prvočíslo?“
Někteří lidé si to myslí, protože říkají, že 1 lze dělit pouze 1 a sebou samým, ale v matematice bylo číslo 1 vyřazeno jako prvočíslo, protože má pouze jednoho dělitele. Ve skutečnosti se k vyloučení čísla 1 ze seznamu prvočísel používá kritérium „celé kladné číslo je prvočíslo, pokud má přesně dva kladné dělitele“. Není to proto, že bychom byli vybíraví, ale kdyby bylo číslo jedna považováno za prvočíslo, pak by se o mnoha matematických vlastnostech muselo mluvit jinak.
Takže jednička je složené číslo?
No, ani složené není, protože ji nelze dosadit jako součin prvočísel. Číslo 1 není ani prvočíslo, ani složené. A než se zeptáte, nula také není prvočíslo ani složené, ale to proto, že všechny úvahy jsme vysvětlovali pro kladná čísla, tedy větší než nula.
Dělitel čísla
Dělitel čísla je hodnota, která dělí číslo na přesné díly, jinými slovy má zbytek 0.
Dělitel čísla je hodnota, která dělí číslo na přesné díly, jinými slovy má zbytek 0.
Na příkladu vypočítáme dělitele čísla 24.
Dělení začneme nejmenšími čísly počínaje číslem 1.
- 24 / 1 = 24.
- Dělení začneme nejmenším číslem počínaje číslem 1. Obě čísla, 1 i 24, jsou děliteli.
- 24 / 2 = 12.
- 24 / 2 = 12. Takže 2 i 12 jsou dělitelé.
- 24 / 3 = 8. Takže 3 i 8 jsou dělitelé.
- 24 / 4 = 6. Takže 4 i 6 jsou dělitelé.
- 24 / 5 = 4. Není to přesné dělení a má zbytek 4, takže 5 není dělitelem.
Dalším číslem je 6, ale protože už víme, že 6 je dělitelem 24, výpočet dělitelů pro 24 jsme dokončili.
Video:
Pokud se chcete dozvědět více o prvočíslech a složených číslech, podívejte se na následující video. Seznámíte se také s pojmem faktorizace pomocí Montessoriho tabulky.
Toto video je jedním z našich interaktivních výukových materiálů, a přestože není interaktivní, můžete se na něj podívat tolikrát, kolikrát budete potřebovat, a sdílet ho s přáteli. Pokud chcete mít přístup k našim interaktivním výukovým lekcím, zaregistrujte se na webu Smartick! Online metoda, která pomáhá dětem ve věku od 4 do 14 let učit se a procvičovat matematiku.
Pokud se chcete dále učit o prvočíslech a nejlépe přizpůsobit matematiku své úrovni, zaregistrujte se u Smartick a vyzkoušejte si ji zdarma!
Další informace:
- Prvočísla a složená čísla
- Prvočísla: A Trick to Help You Identify Them
- Prime Numbers: Jak je najít pomocí Eratosthenova síta
- Naučte se, jak vynásobit prvočísla
- Úkoly pro prvočísla se Smartickem



- Autor
- Nejnovější příspěvky
Multidisciplinární a multikulturní tým složený z matematiků, učitelů, profesorů a dalších odborníků v oblasti vzdělávání!
Snaží se vytvářet ten nejlepší možný matematický obsah.
- Příklady slovních úloh z matematiky pro 3. třídu s řešením – 25. 3. 2021
- Pořadové vnitřní úhly: Co to jsou a jak je najít s příklady – 03/11/2021
- Příklady slovních úloh pro 2. stupeň ZŠ s řešením – 02/04/2021