Závislé vs. nezávislé události
Před několika příspěvky jsem začal mluvit o pravděpodobnosti. Chci tomuto tématu věnovat více času, protože je to jeden z těch pojmů, které mohou být v jednu chvíli zjevně jednoduché a v další chvíli přímo matoucí.
Kdykoli přistupujete k problému pravděpodobnosti zahrnujícímu více než jednu událost, začněte tím, že si položíte otázku, zda jsou události závislé nebo nezávislé, tj. mění jedna událost pravděpodobnost druhé události? Mění první událost, která nastane, celý systém?“
(Tažení více karet z balíčku bez výměny je klasickým příkladem závislé události. Když si vytáhneme první kartu, systém se změní z 52 možných variant na 51, než nastane druhá událost)
V reálném životě mají lidé tendenci neustále zaměňovat závislost. Například si hodíte spravedlivou mincí. Desetkrát za sebou padne hlava. Jste si jisti, že příští hod bude určitě orel…je to tak?“
Jaká je pravděpodobnost, že příští mince bude opět hlava?“
Stále je to 1/2. Je to pravděpodobnost, že příští mince bude opět hlava. Hod mincí je nezávislá událost. Jinými slovy, výsledek dalšího hodu není ovlivněn tím, co se stalo předtím. Je to, jako by to bylo poprvé, co jste si hodili mincí. Pravděpodobnost se nemění.
Proč se tedy „zdá“, že by to měl být orel?“
Máme tendenci přemýšlet o událostech dohromady, a ne jednotlivě. Ačkoli pravděpodobnost hodu hlavou zůstává pro každý hod stejná, kombinovaná šance, že padne 11 hlav za sebou, je malá.
Počítejme ji.
V předchozí lekci pravděpodobnosti jsme se naučili, že když spojíme více událostí dohromady a chceme, aby všechny nastaly (scénář „a“), musíme jejich pravděpodobnosti vynásobit dohromady.
Protože každý hod mincí má pravděpodobnost hlavy rovnu 1/2, musím prostě jedenáctkrát vynásobit dohromady 1/2.
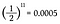
To je 0,05% šance, že padne jedenáct hlav za sebou! Ale než si s úlevou vydechnete a řeknete: „Vidíte, já to věděl!“, spočítejme si, jaká je pravděpodobnost, že při jedenáctém hodu padne místo hlavy ocas.
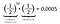
Ano, je to tak. Je stejně pravděpodobné, že padne deset hlav následovaných ocáskem, jako že padne jedenáct hlav za sebou. Ve skutečnosti, protože individuální pravděpodobnost, že padne hlava, je stejná jako pravděpodobnost, že padne ocas, každé uspořádání 11 hodů mincí povede ke stejné pravděpodobnosti 0,0005. Každé uspořádání je stejně pravděpodobné.
Takže… proč se vám „zdá“ nepravděpodobné hodit deset hlav za sebou?“
Běžná mylná představa není způsobena pravděpodobností, ale nepochopením kombinatoriky a permutací.
Dosud jsme zjistili, že:
- Pravděpodobnost, že padne hlava nebo orel, je při každém jednotlivém hodu stejně pravděpodobná: P(H) = P(T) = 1/2.
- Každé jedinečné uspořádání (permutace) možných hodů mincí je stejně pravděpodobné.
Co z toho vyplývá?
Poznání výběrového prostoru
Výběrový prostor je jednoduše výčet všech možných uspořádání (permutací) výsledků. Protože výběrový prostor pro 11 po sobě jdoucích hodů mincí je poměrně velký, prozkoumejme místo toho jednodušší případ.
Vzorový prostor pro čtyři hody mincí je:

Intuitivně si můžeme myslet: Je pravděpodobnější, že ze čtyř hodů padnou 2 hlavy a 2 ořechy než všechny hlavy nebo všechny ořechy.
A to je pravda.
Víme, že každá ze šestnácti permutací je stejně pravděpodobná, protože P(H) = P(T) = 1/2. Víme, že každá ze šestnácti permutací je stejně pravděpodobná. Každá permutace má tedy stejnou pravděpodobnost:

Poznámka: Protože výběrový prostor představuje všechny možné výsledky, součet všech pravděpodobností je vždy roven 1 (Např. 0,0625 – 16 = 1).
Podíváme-li se na náš výběrový prostor, kolik různých permutací hodu mincí vede k libovolné kombinaci 0f 2 hlavy a 2 ořechy?

Všimněte si, že 6 z 16 možných výsledků vede ke kombinaci 2 hlavy a 2 ocasy. Protože jakákoli z těchto šesti permutací splňuje naše kritéria, je to považováno za scénář „nebo“ – takže pravděpodobnosti sečtěte (nebo jednoduše vynásobte 6, protože jsou všechny stejné).
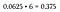
To je 37,5% pravděpodobnost, že hodíme kombinaci dvou hlav a dvou ocasů, což je mnohem více než pravděpodobnost, že hodíme všechny hlavy nebo všechny ocasy (která zůstává 6.25 % pro každou z nich, protože v našem výběrovém prostoru existuje pouze jedna permutace každé z nich).
Proto intuitivně víme, že je pravděpodobnější hodit stejný počet hlav a ocasů než hodit všechny jednoho druhu, přičemž stále platí, že události jsou nezávislé, přičemž jednotlivé hody a permutace mají stejnou pravděpodobnost výskytu.
Permutace & Kombinace
Velká část úspěšného výpočtu pravděpodobnosti spočívá v důkladném pochopení permutací a kombinací. Tam tedy zamíříme příště!