Abhängige vs. unabhängige Ereignisse
Vor ein paar Beiträgen habe ich begonnen, über Wahrscheinlichkeiten zu sprechen. Ich möchte etwas mehr Zeit auf das Thema verwenden, weil es eines jener Konzepte ist, die in der einen Minute offensichtlich einfach und in der nächsten geradezu verwirrend sein können.
Wann immer Sie sich einem Wahrscheinlichkeitsproblem nähern, das mehr als ein Ereignis beinhaltet, beginnen Sie damit, sich zu fragen, ob die Ereignisse abhängig oder unabhängig sind, d.h. verändert ein Ereignis die Wahrscheinlichkeit des anderen Ereignisses? Verändert das erste Ereignis das System?
(Das Ziehen mehrerer Karten aus einem Stapel ohne Ersatz ist ein klassisches Beispiel für ein abhängiges Ereignis. Wenn wir die erste Karte ziehen, ändert sich das System von 52 möglichen Optionen auf 51, bevor das zweite Ereignis eintritt.)
Im wirklichen Leben neigen Menschen dazu, Abhängigkeiten ständig zu verwechseln. Zum Beispiel wirft man eine Münze. Sie fällt 10 Mal hintereinander auf Kopf. Sie sind sich sicher, dass der nächste Wurf Schwanz sein wird…
Wie hoch ist die Wahrscheinlichkeit, dass die nächste Münze wieder Kopf ist?
Sie ist immer noch 1/2. Das Werfen einer Münze ist ein unabhängiges Ereignis. Mit anderen Worten: Das Ergebnis des nächsten Wurfs wird nicht von dem beeinflusst, was vorher passiert ist. Es ist so, als ob man die Münze zum ersten Mal wirft. Die Wahrscheinlichkeit ist unverändert.
Warum „fühlt“ es sich dann so an, als sollte es Zahl sein?
Wir neigen dazu, die Ereignisse zusammen und nicht einzeln zu betrachten. Obwohl die Wahrscheinlichkeit, Kopf zu werfen, bei jedem Wurf gleich bleibt, ist die kombinierte Chance, 11 Mal hintereinander Kopf zu werfen, gering.
Lassen Sie uns das berechnen.
Wir haben in der vorherigen Lektion über Wahrscheinlichkeit gelernt, dass wir die Wahrscheinlichkeiten mehrerer Ereignisse miteinander multiplizieren müssen, wenn wir wollen, dass sie alle eintreten (das „und“-Szenario).
Da jeder Münzwurf eine Wahrscheinlichkeit von Kopf gleich 1/2 hat, muss ich einfach elfmal 1/2 miteinander multiplizieren.
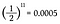
Das ist eine Wahrscheinlichkeit von 0,05%, elfmal hintereinander Kopf zu werfen! Aber bevor du erleichtert aufatmest und sagst: „Siehst du, ich wusste es!“, lass uns die Wahrscheinlichkeit berechnen, beim elften Wurf stattdessen eine Zahl zu erhalten.
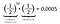
Ja, das stimmt. Es ist genauso wahrscheinlich, zehnmal Kopf zu werfen, gefolgt von einer Zahl, wie elfmal Kopf zu werfen. Da die individuelle Wahrscheinlichkeit, Kopf zu werfen, die gleiche ist wie die Wahrscheinlichkeit, Zahl zu werfen, ergibt jede Anordnung von 11 Münzwürfen die gleiche Wahrscheinlichkeit von 0,0005. Jede Anordnung ist gleich wahrscheinlich.
Warum „fühlt“ es sich dann so unwahrscheinlich an, zehnmal hintereinander Kopf zu werfen?
Der weit verbreitete Irrtum hat nichts mit Wahrscheinlichkeit zu tun, sondern mit einem falschen Verständnis von Kombinatorik und Permutationen.
Bislang haben wir festgestellt, dass:
- Die Wahrscheinlichkeit, Kopf oder Zahl zu werfen, ist bei jedem einzelnen Wurf gleich groß: P(H) = P(T) = 1/2.
- Jede einzelne Anordnung (Permutation) der möglichen Münzwürfe ist gleich wahrscheinlich.
Was ergibt sich daraus?
Verständnis des Stichprobenraums
Der Stichprobenraum ist einfach eine Auflistung aller möglichen Ergebnisanordnungen (Permutationen). Da der Stichprobenraum für 11 aufeinanderfolgende Münzwürfe ziemlich groß ist, wollen wir stattdessen einen einfacheren Fall untersuchen.
Der Stichprobenraum für vier Münzwürfe ist:

Intuitiv könnte man denken: Es ist wahrscheinlicher, dass bei vier Würfen 2 Mal Kopf und 2 Mal Zahl fällt als nur Kopf oder nur Zahl.
Und das stimmt. Rechnen wir mal nach.
Wir wissen, dass jede der sechzehn Permutationen gleich wahrscheinlich ist, weil P(H) = P(T) = 1/2. Also hat jede Permutation die gleiche Wahrscheinlichkeit:

Anmerkung: Da der Stichprobenraum alle möglichen Ergebnisse repräsentiert, ist die Summe aller Wahrscheinlichkeiten immer gleich 1 (z.B. 0,0625 – 16 = 1).
Betrachtet man unseren Stichprobenraum, wie viele verschiedene Permutationen des Münzwurfs ergeben eine beliebige Kombination von 2 Kopf und 2 Zahl?

Beachte, dass 6 von 16 möglichen Ergebnissen zu einer Kombination aus zwei Köpfen und zwei Zahlen führen. Da jede dieser sechs Permutationen unsere Kriterien erfüllt, wird dies als ein „oder“-Szenario betrachtet – addieren Sie also die Wahrscheinlichkeiten zusammen (oder multiplizieren Sie einfach mit 6, da sie alle gleich sind).
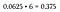
Das ist eine 37,5%ige Chance, eine Kombination aus 2 Köpfen und 2 Zahlen zu werfen, was weitaus größer ist als die Wahrscheinlichkeit, alle Köpfe oder alle Zahlen zu werfen (die immer noch 6.
Aus diesem Grund wissen wir intuitiv, dass es wahrscheinlicher ist, eine gleiche Anzahl von Kopf und Zahl zu werfen, als alle von einer Sorte zu werfen, wobei die Tatsache erhalten bleibt, dass die Ereignisse unabhängig sind und die einzelnen Würfe und Permutationen gleich wahrscheinlich sind.
Permutationen & Kombinationen
Ein Großteil der erfolgreichen Berechnung von Wahrscheinlichkeiten besteht darin, Permutationen und Kombinationen gründlich zu verstehen. Das ist also unser nächster Schritt!