Sammenligninger for SHM
Overvej en blok, der er fastgjort til en fjeder på et friktionsfrit bord (Figur \(\PageIndex{3}\)). Ligevægtspositionen (den position, hvor fjederen hverken er strakt eller trykket sammen) er markeret som x = 0 . I ligevægtspositionen er nettokraften nul.
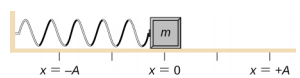
Der udføres arbejde på blokken for at trække den ud til en position x = + A, og den frigøres derefter fra hvilepositionen. Den maksimale x-position (A) kaldes bevægelsens amplitude. Klodsen begynder at svinge i SHM mellem x = + A og x = -A, hvor A er bevægelsens amplitude, og T er svingningens periode. Perioden er tiden for en svingning. Figur \(\PageIndex{4}\) viser blokens bevægelse, mens den fuldfører halvanden svingning efter udløsningen.
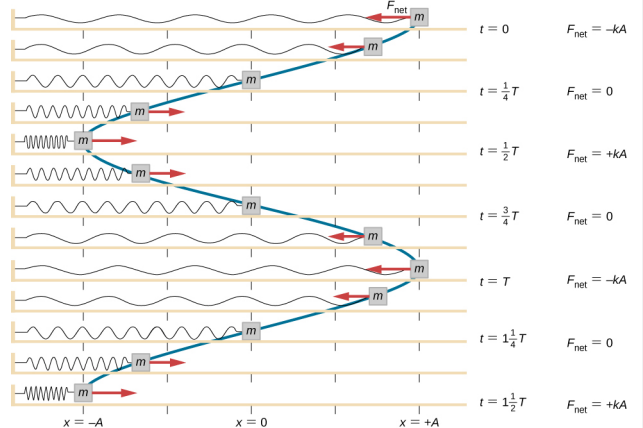
\
Ligningen for positionen som funktion af tiden \(x(t) = A\cos( \omega t)\) er god til modellering af data, hvor klodsens position til begyndelsestidspunktet t = 0,00 s er på amplituden A, og begyndelseshastigheden er nul. Når der tages eksperimentelle data, er massens position på begyndelsestidspunktet t = 0,00 s ofte ikke lig med amplituden, og begyndelseshastigheden er ikke nul. Betragt 10 sekunders data indsamlet af en studerende i laboratoriet, som er vist i figur \(\PageIndex{6}\).
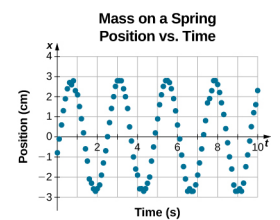
Dataene i figur \(\PageIndex{6}\) kan stadig modelleres med en periodisk funktion, som f.eks. en cosinusfunktion, men funktionen er forskudt til højre. Denne forskydning er kendt som en faseforskydning og repræsenteres normalt ved det græske bogstav phi (\(\(\phi\))). Ligningen for positionen som en funktion af tiden for en blok på en fjeder bliver
\
Dette er den generaliserede ligning for SHM, hvor t er tiden målt i sekunder, \(\omega\) er vinkelfrekvensen med enheder af inverse sekunder, A er amplituden målt i meter eller centimeter, og \(\phi\) er faseforskydningen målt i radianer (Figur \(\PageIndex{7}\)). Det skal bemærkes, at da sinus- og cosinusfunktioner kun adskiller sig ved en faseforskydning, kan denne bevægelse modelleres ved hjælp af enten cosinus- eller sinusfunktionen.
Hastigheden af en masse på en fjeder, der svinger i SHM, kan findes ved at tage den afledte af positionsligningen:
\
Da sinusfunktionen svinger mellem -1 og +1, er den maksimale hastighed amplituden gange vinkelfrekvensen, vmax = A\(\omega\). Den maksimale hastighed opstår ved ligevægtspositionen (x = 0), når massen bevæger sig mod x = + A. Den maksimale hastighed i negativ retning opnås ved ligevægtspositionen (x = 0), når massen bevæger sig mod x = -A og er lig med -vmax.
Massens acceleration på fjederen kan findes ved at tage den tidsafledte af hastigheden:
\