Beregning af ΔS ud fra termodynamiske cyklusser
Vi kan også beregne en ændring i entropi ved hjælp af en termodynamisk cyklus. Som du tidligere har lært, er den molære varmekapacitet (Cp) den varmemængde, der er nødvendig for at hæve temperaturen af 1 mol af et stof med 1 °C ved konstant tryk. På samme måde er Cv den varmemængde, der er nødvendig for at øge temperaturen af 1 mol af et stof med 1 °C ved konstant volumen. Stigningen i entropien med stigende temperatur i figur \(\PageIndex{2}\) er omtrent proportional med stoffets varmekapacitet.
Husk, at entropiforandringen (ΔS) er relateret til varmestrømmen (qrev) ved ΔS = qrev/T. Da qrev = nCpΔT ved konstant tryk eller nCvΔT ved konstant volumen, hvor n er antallet af mol af det tilstedeværende stof, er ændringen i entropi for et stof, hvis temperatur ændres fra T1 til T2, som følger:
\
Som du vil opdage i mere avancerede matematikkurser, end det kræves her, kan det vises, at dette er lig med følgende:For en gennemgang af naturlige logaritmer, se Essential Skills 6 i kapitel 11 “Liquids”.
\
Sådan kan vi
Så kan vi bruge en kombination af målinger af varmekapacitet (ligning 18.20 eller ligning 18.21) og eksperimentelt målte værdier af fusions- eller fordampningsenthalpier, hvis der er tale om en faseændring (ligning 18.18) til at beregne entropiændringen svarende til en ændring i temperaturen af en prøve.
Vi kan bruge en termodynamisk cyklus til at beregne entropiændringen, når faseændringen for et stof som f.eks. svovl ikke kan måles direkte. Som nævnt i øvelsen i eksempel 6 findes elementært svovl i to former (del (a) i figur \(\PageIndex{3}\)): en orthorhombisk form med en meget velordnet struktur (Sα) og en mindre velordnet monoklin form (Sβ). Den orthorhombiske (α) form er mere stabil ved stuetemperatur, men undergår en faseovergang til den monokliniske (β) form ved temperaturer over 95,3 °C (368,5 K). Overgangen fra Sα til Sβ kan beskrives ved den termodynamiske cyklus, der er vist i del (b) i figur \(\PageIndex{3}\), hvor flydende svovl er et mellemprodukt. Den ændring i entropi, der ledsager omdannelsen af flydende svovl til Sβ (-ΔSfus(β) = ΔS3 i cyklusen), kan ikke måles direkte. Da entropi er en tilstandsfunktion, kan ΔS3 imidlertid beregnes ud fra den samlede entropiændring (ΔSt) for Sα-Sβ-overgangen, som er lig med summen af ΔS-værdierne for trinene i den termodynamiske cyklus, ved hjælp af ligning 18.20 og tabulerede termodynamiske parametre (varmekapaciteterne for Sα og Sβ, ΔHfus(α), og Sα’s smeltepunkt.)

Løsning for ΔS3 giver en værdi på -3,24 J/(mol-K). Som forventet for omdannelsen af en mindre ordnet tilstand (en væske) til en mere ordnet tilstand (en krystal) er ΔS3 negativ.
Hvordan måles entropier
Den absolutte entropi for et stof ved en hvilken som helst temperatur over 0 K skal bestemmes ved at beregne de stigninger i varme q, der kræves for at bringe stoffet fra 0 K til den ønskede temperatur, og derefter summere forholdet q/T. Der er behov for to slags eksperimentelle målinger:
- De enthalpier, der er forbundet med eventuelle faseændringer, som stoffet kan undergå inden for det pågældende temperaturområde. Smeltning af et fast stof og fordampning af en væske svarer til betydelige stigninger i antallet af mikrotilstande, der er tilgængelige til at modtage termisk energi, så når disse processer finder sted, vil energi strømme ind i et system og fylde disse nye mikrotilstande i det omfang, det er nødvendigt for at opretholde en konstant temperatur (fryse- eller kogepunktet); disse indstrømninger af termisk energi svarer til fusions- og fordampningsvarmene. Den entropistigning, der er forbundet med smeltning, er f.eks. blot ΔHfusion/Tm.
- Varmekapaciteten C for en fase udtrykker den varmemængde, der kræves for at ændre temperaturen med en lille mængde ΔT , eller mere præcist med en infinitesimal mængde dT . Den entropistigning, der fremkaldes ved opvarmning af et stof over et temperaturinterval, som ikke omfatter en faseovergang, er således givet ved summen af størrelserne C dT/T for hvert temperaturforøgelse dT . Dette er naturligvis blot integralet
\
Da varmekapaciteten i sig selv er lidt temperaturafhængig, kræver de mest præcise bestemmelser af absolutte entropier, at den funktionelle afhængighed af C af T anvendes i ovenstående integral i stedet for en konstant C.
\
Når dette ikke er kendt, kan man foretage en række målinger af varmekapaciteten over snævre temperaturintervaller ΔT og måle arealet under hvert afsnit af kurven.
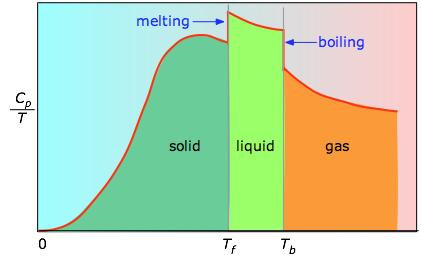
Arealet under hvert afsnit i diagrammet repræsenterer den entropiændring, der er forbundet med opvarmning af stoffet gennem et interval ΔT. Hertil skal lægges enthalpierne for smeltning, fordampning og for eventuelle fast-fast-faseændringer. Værdierne af Cp for temperaturer nær nul måles ikke direkte, men kan estimeres ud fra kvanteteori.
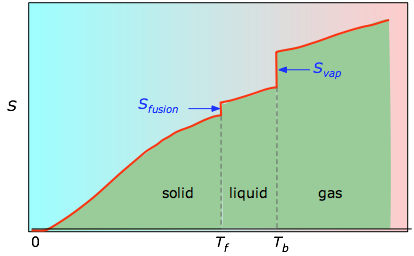
De kumulative områder fra 0 K til en given temperatur (taget fra det eksperimentelle plot til venstre) plottes derefter som en funktion af T, og eventuelle faseændringsentropier som Svap = Hvap / Tb lægges sammen for at opnå den absolutte entropi ved temperaturen T.