The Aufbau Principle
For at bestemme elektronkonfigurationen for et bestemt atom kan vi “opbygge” strukturerne i rækkefølge efter atomnummer. Vi begynder med brint og fortsætter gennem perioderne i det periodiske system, idet vi tilføjer en proton ad gangen til kernen og en elektron til den rette underskal, indtil vi har beskrevet elektronkonfigurationen for alle grundstofferne. Denne fremgangsmåde kaldes Aufbau-princippet, fra det tyske ord Aufbau (“at bygge op”). Hver elektron, der tilføjes, besætter den underskal med den laveste tilgængelige energi (i den rækkefølge, der er vist i figur \(\PageIndex{3}\)), med forbehold af de begrænsninger, der er pålagt af de tilladte kvantetal i henhold til Pauli-eksklusionsprincippet. Elektroner indtræder først i underskaller med højere energi, når underskaller med lavere energi er blevet fyldt op til deres fulde kapacitet. Figur \(\PageIndex{3}\) illustrerer den traditionelle måde at huske fyldningsrækkefølgen for atomorbitaler.
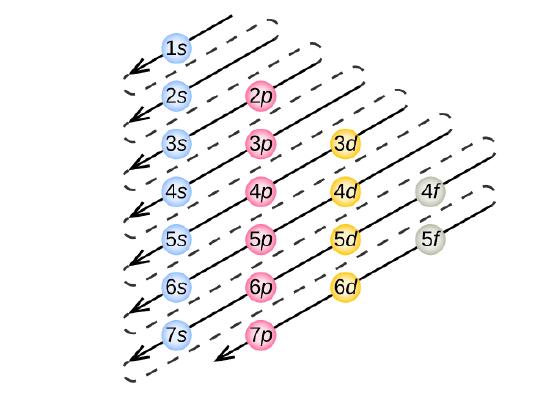
Da opstillingen af det periodiske system er baseret på elektronkonfigurationer, giver figur \(\PageIndex{4}\) en alternativ metode til at bestemme elektronkonfigurationerne. Påfyldningsrækkefølgen begynder simpelthen ved hydrogen og omfatter hver underskal, efterhånden som man fortsætter i stigende Z-orden. F.eks. ser vi efter at have fyldt 3p-blokken op til Ar, at orbitalet vil være 4s (K, Ca), efterfulgt af 3d-orbitalerne.
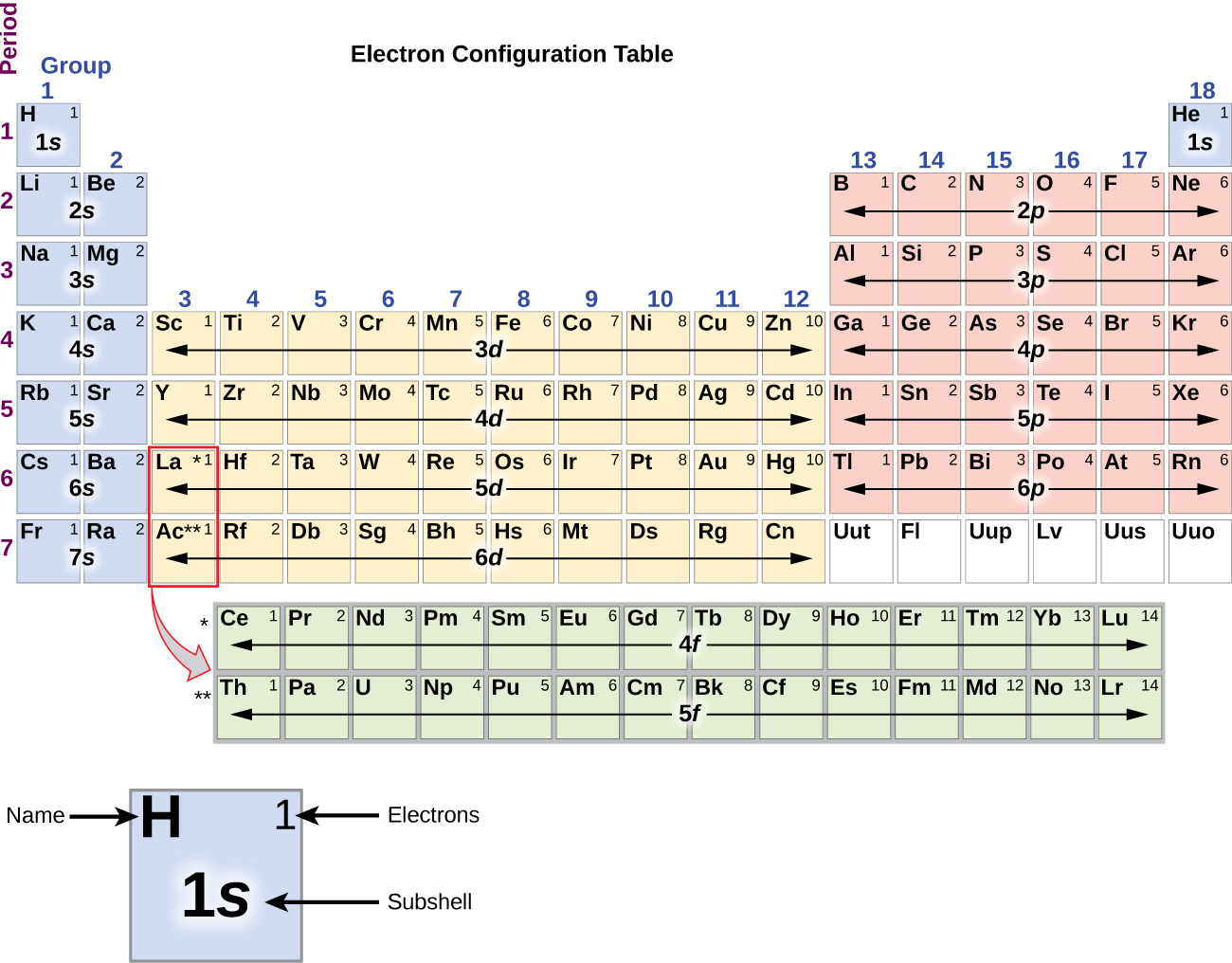
Vi vil nu konstruere grundtilstandens elektronkonfiguration og orbitaldiagrammet for et udvalg af atomer i den første og anden periode i det periodiske system. Orbitaldiagrammer er billedlige repræsentationer af elektronkonfigurationen, der viser de enkelte orbitaler og elektronernes parringsarrangement. Vi starter med et enkelt hydrogenatom (atomnummer 1), som består af en proton og en elektron. Hvis vi henviser til enten figur \(\PageIndex{3}\) eller \(\PageIndex{4}\), vil vi forvente at finde elektronen i 1s orbitalet. Konventionelt udfyldes værdien \(m_s=+\dfrac{1}{2}\) normalt først. Elektronkonfigurationen og orbitaldiagrammet er:
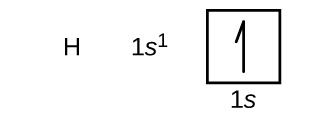
Efter brint følger ædelgassen helium, som har atomnummer 2. Heliumatomet indeholder to protoner og to elektroner. Den første elektron har de samme fire kvantetal som brintatomets elektron (n = 1, l = 0, ml = 0, \(m_s=+\dfrac{1}{2}\)). Den anden elektron går også ind i 1s orbitalet og fylder dette orbital. Den anden elektron har de samme n, l og ml kvantetal, men skal have det modsatte spinkvantetal, \(m_s=-\dfrac{1}{2}\). Dette er i overensstemmelse med Pauli-eksklusionsprincippet: Ingen to elektroner i det samme atom kan have det samme sæt af fire kvantetal. For orbitaldiagrammer betyder det, at der skal gå to pile i hver kasse (som repræsenterer to elektroner i hver orbital), og at pilene skal pege i modsatte retninger (som repræsenterer parrede spins). Elektronkonfigurationen og orbitaldiagrammet for helium er:
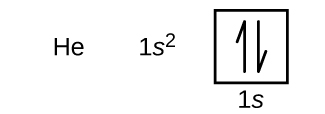
Den n = 1-skal er fuldstændig fyldt i et heliumatom.
Det næste atom er alkalimetallet lithium med atomnummer 3. De to første elektroner i lithium fylder 1s-bobitalet og har de samme sæt af fire kvantetal som de to elektroner i helium. Den resterende elektron skal besætte den næstlaveste energibital, 2s-bobitalet (figur \(\PageIndex{3}\) eller \(\(\PageIndex{4}\))). Elektronkonfigurationen og orbitaldiagrammet for lithium er således:
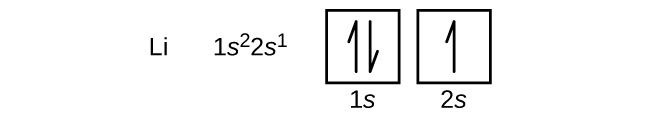
Et atom af det alkaliske jordarmetal beryllium med atomnummer 4 indeholder fire protoner i kernen og fire elektroner omkring kernen. Den fjerde elektron fylder den resterende plads i 2s-bobitalet.
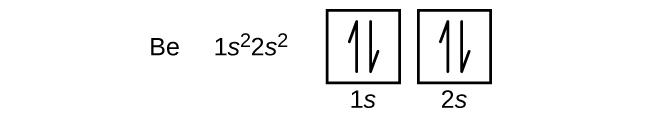
Et atom af bor (atomnummer 5) indeholder fem elektroner. N = 1 skallen er fyldt med to elektroner, og tre elektroner vil besætte n = 2 skallen. Da enhver s-underskal kun kan indeholde to elektroner, må den femte elektron besætte det næste energiniveau, som vil være en 2p-orbital. Der findes tre degenererede 2p-orbitaler (ml = -1, 0, +1), og elektronen kan indtage et hvilket som helst af disse p-orbitaler. Når vi tegner orbitaldiagrammer, medtager vi tomme kasser for at afbilde eventuelle tomme orbitaler i den samme underskal, som vi udfylder.

Kulstof (atomnummer 6) har seks elektroner. Fire af dem fylder 1s og 2s orbitalerne. De resterende to elektroner besætter 2p-underskallen. Vi har nu valget mellem at fylde en af 2p-orbitalerne og parre elektronerne eller at lade elektronerne stå uparret i to forskellige, men degenererede p-orbitaler. Orbitalerne fyldes som beskrevet i Hunds regel: Den lavenergikonfiguration for et atom med elektroner i et sæt degenererede orbitaler er den, der har det maksimale antal uparrede elektroner. De to elektroner i kulstofets 2p-orbitaler har således identiske n, l og ms kvantetal og adskiller sig fra hinanden ved deres ml kvantetal (i overensstemmelse med Pauli-eksklusionsprincippet). Elektronkonfigurationen og orbitaldiagrammet for kulstof er:

Stickstof (atomnummer 7) fylder 1s og 2s delskaller og har en elektron i hver af de tre 2p-orbitaler i overensstemmelse med Hund’s regel. Disse tre elektroner har uparrede spins. Oxygen (atomnummer 8) har et elektronpar i en hvilken som helst af 2p-orbitalerne (elektronerne har modsatrettede spins) og en enkelt elektron i hver af de to andre. Fluor (atomnummer 9) har kun én 2p-orbital, der indeholder en uparret elektron. Alle elektronerne i ædelgassen neon (atomnummer 10) er parrede, og alle orbitalerne i n = 1 og n = 2 skallerne er fyldte. Elektronkonfigurationer og orbitaldiagrammer for disse fire grundstoffer er:
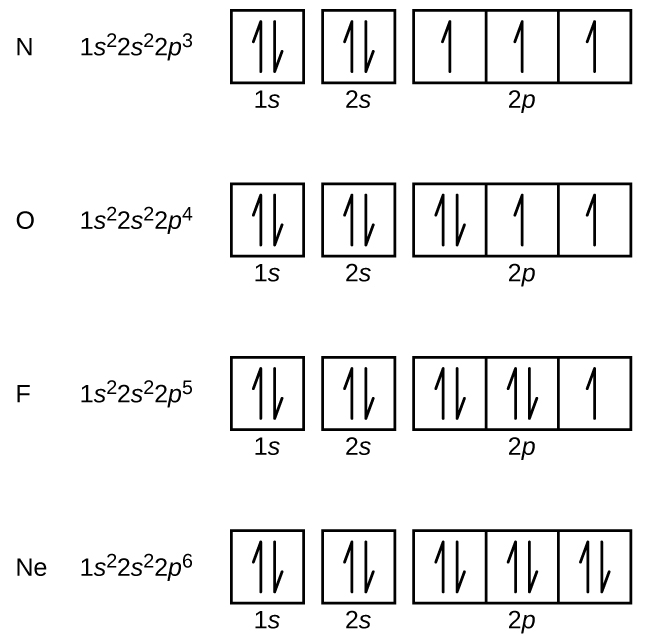
Alkalimetallet natrium (atomnummer 11) har én elektron mere end neonatomet. Denne elektron skal gå ind i den lavenergiunderskal, der er tilgængelig, 3s orbitalet, hvilket giver en 1s22s22p63s1 konfiguration. De elektroner, der besætter de(n) yderste skalorbital(er) (højeste værdi af n), kaldes valenselektroner, og de elektroner, der besætter de indre skalorbital(er), kaldes kerneelektroner ( Figur \PageIndex5\PageIndex5). Da kerneelektronernes skaller svarer til ædelgasens elektronkonfigurationer, kan vi forkortere elektronkonfigurationer ved at skrive den ædelgas, der svarer til kerneelektronkonfigurationen, sammen med valenselektronerne i et kondenseret format. I vores eksempel med natrium repræsenterer symbolet kerneelektroner (1s22s22p6), og vores forkortede eller kondenserede konfiguration er 3s1.

Sådan kan den forkortede konfiguration for lithium fremstilles som 2s1, hvor den repræsenterer heliumatomets konfiguration, som er identisk med den for lithiums fyldte indre skal. Ved at skrive konfigurationer på denne måde understreges ligheden mellem lithiums og natriums konfigurationer. Begge atomer, som tilhører alkalimetallfamilien, har kun én elektron i en valenssubskal uden for et fyldt sæt indre skaller.
\}\,2s^1\\\\ \ce{Na:}\,3s^1\]
Det alkaliske jordalkalimetal magnesium (atomnummer 12) er med sine 12 elektroner i en 3s2-konfiguration analogt med familiemedlemmet beryllium, 2s2. Begge atomer har en fyldt s-delskal uden for deres fyldte indre skaller. Aluminium (atomnummer 13), med 13 elektroner og elektronkonfiguration 3s23p1, svarer til dets familiemedlem bor, 2s22p1.
Elektronkonfigurationen af silicium (14 elektroner), fosfor (15 elektroner), svovl (16 elektroner), klor (17 elektroner) og argon (18 elektroner) svarer i elektronkonfigurationen af deres ydre skaller til deres tilsvarende familiemedlemmer henholdsvis kulstof, nitrogen, oxygen, fluor og neon, bortset fra at hovedkvantetallet i den ydre skal for de tungere grundstoffer er steget med én til n = 3. Figur \(\PageIndex{6}\) viser den lavenergi- eller grundtilstands-elektronkonfiguration for disse grundstoffer samt den for atomer af hvert af de kendte grundstoffer.
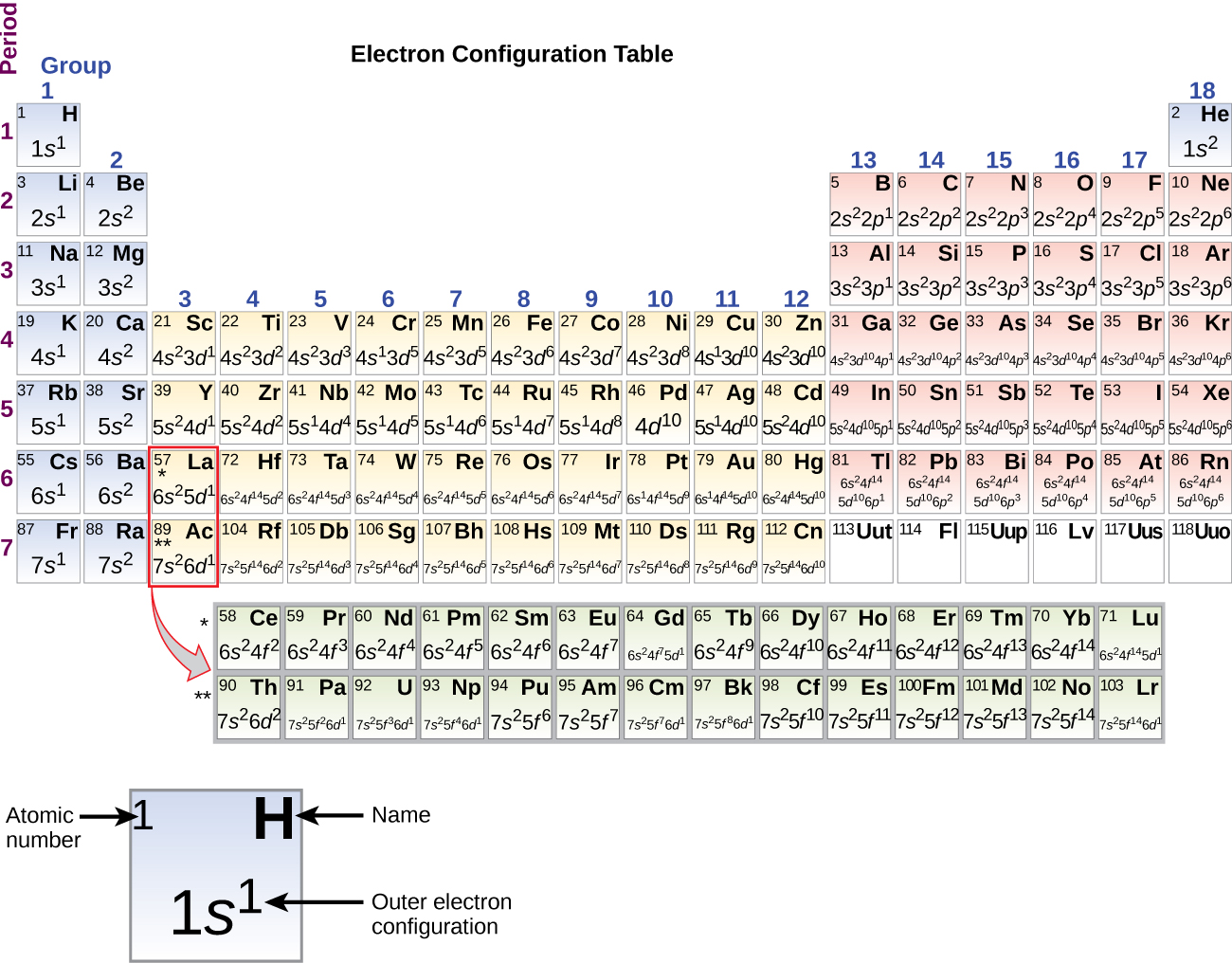
Når vi kommer til det næste grundstof i det periodiske system, alkalimetallet kalium (atomnummer 19), kunne vi forvente, at vi ville begynde at tilføje elektroner til 3d-underskallen. Alle tilgængelige kemiske og fysiske beviser tyder imidlertid på, at kalium er ligesom lithium og natrium, og at den næste elektron ikke føjes til 3d-niveauet, men i stedet føjes til 4sniveauet (figur \(\(\PageIndex{3}\) eller \(\(\PageIndex{4}\))). Som tidligere omtalt er 3d-orbitalet uden radiale knuder højere i energi, fordi det er mindre gennemtrængende og mere afskærmet fra kernen end 4s-båndet, som har tre radiale knuder. Kalium har således en elektronkonfiguration på 4s1. Kalium svarer derfor til Li og Na i sin valensskalkonfiguration. Den næste elektron tilføjes for at fuldende 4s-subskallen, og calcium har en elektronkonfiguration på 4s2. Dette giver calcium en ydre skal-elektronkonfiguration svarende til beryllium og magnesiums.
Af begyndelse med overgangsmetallet scandium (atomnummer 21) tilføjes der successivt yderligere elektroner til 3d-underskallen. Denne underskal er fyldt til sin kapacitet med 10 elektroner (husk, at for l = 2 , er der 2l + 1 = 5 værdier af ml, hvilket betyder, at der er fem d-orbitaler, der tilsammen har en kapacitet på 10 elektroner). 4p-underskallen er den næste, der fyldes. Bemærk, at for tre serier af grundstoffer, scandium (Sc) gennem kobber (Cu), yttrium (Y) gennem sølv (Ag) og lutetium (Lu) gennem guld (Au), tilføjes der successivt i alt 10 d-elektroner til (n – 1)-skallen ved siden af n-skallen for at bringe denne (n – 1)-skal fra 8 til 18 elektroner. For to serier, lanthan (La) gennem lutetium (Lu) og actinium (Ac) gennem lawrencium (Lr), tilføjes 14 f-elektroner (l = 3, 2l + 1 = 7 ml-værdier; således syv orbitaler med en samlet kapacitet på 14 elektroner) successivt til (n – 2)-skallen for at bringe denne skal fra 18 elektroner til i alt 32 elektroner.
Eksempel \(\PageIndex{1}\): Kvantetal og elektronkonfigurationer
Hvad er elektronkonfigurationen og orbitaldiagrammet for et fosforatom? Hvad er de fire kvantetal for den sidste elektron, der er tilføjet?
Løsning
Atomnummeret for fosfor er 15. Et fosforatom indeholder således 15 elektroner. Rækkefølgen af fyldningen af energiniveauerne er 1s, 2s, 2p, 3s, 3p, 4s, . . . . Fosforatomets 15 elektroner vil fylde op til 3p-orbitalet, som vil indeholde tre elektroner:
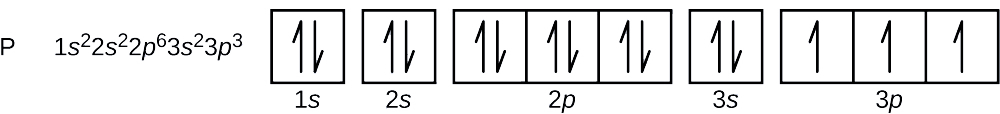
Den sidste elektron, der tilføjes, er en 3p-elektron. Derfor er n = 3, og for en p-type orbital er l = 1. ml-værdien kunne være -1, 0 eller +1. De tre p-orbitaler er degenererede, så en hvilken som helst af disse ml-værdier er korrekt. For uparrede elektroner tildeler konventionen værdien \(+\dfrac{1}{2}{2}\) for spinkvantetallet; således \(m_s=+\dfrac{1}{2}{2}\).
Ovelse \(\(\PageIndex{1}\)
Identificer atomerne ud fra de givne elektronkonfigurationer:
- 4s23d5
- 5s24d105p6
Svar a
Mn
Svar b
Xe
Det periodiske system kan være et effektivt redskab til at forudsige elektronkonfigurationen for et grundstof. Vi finder dog undtagelser fra rækkefølgen for fyldning af orbitaler, som er vist i figur \(\PageIndex{3}\) eller \(\(\PageIndex{4}\). F.eks. er elektronkonfigurationen for bl.a. overgangsmetallerne chrom (Cr; atomnummer 24) og kobber (Cu; atomnummer 29) ikke den, som vi ville forvente. Generelt involverer sådanne undtagelser delskaller med meget ens energi, og små effekter kan føre til ændringer i rækkefølgen af fyldning.
For Cr og Cu finder vi, at halvt fyldte og helt fyldte delskaller tilsyneladende repræsenterer forhold med foretrukken stabilitet. Denne stabilitet er sådan, at en elektron skifter fra 4s til 3d orbitalet for at opnå den ekstra stabilitet af en halvfyldt 3d underskal (i Cr) eller en fyldt 3d underskal (i Cu). Der forekommer også andre undtagelser. For eksempel forudsiges niobium (Nb, atomnummer 41) at have elektronkonfiguration 5s24d3. Eksperimentelt observerer vi, at dens elektronkonfiguration i grundtilstanden faktisk er 5s14d4. Vi kan rationalisere denne observation ved at sige, at den elektron-elektron-repulsion, der opstår ved at parre elektronerne i 5sorbitalen, er større end energiforskellen mellem 5s- og 4d-orbitalen. Der findes ingen enkel metode til at forudsige undtagelserne for atomer, hvor størrelsen af repulsionerne mellem elektronerne er større end de små energiforskelle mellem underskaller.