Afhængige og uafhængige hændelser
For et par indlæg siden begyndte jeg at tale om sandsynligheder. Jeg vil bruge lidt mere tid på emnet, fordi det er et af de begreber, der kan være åbenlyst let det ene øjeblik og ligefrem forvirrende det næste.
Når du nærmer dig et sandsynlighedsproblem, der involverer mere end én begivenhed, skal du begynde med at spørge dig selv, om begivenhederne er afhængige eller uafhængige, dvs. om den ene begivenhed ændrer sandsynligheden for den anden begivenhed? Ændrer den første hændelse systemet?
(At trække flere kort fra et spil uden udskiftning er et klassisk eksempel på en afhængig hændelse. Når vi trækker det første kort, ændres systemet fra 52 mulige muligheder til 51 muligheder, inden den anden begivenhed indtræffer.)
I det virkelige liv har mennesker en tendens til at forveksle afhængighed hele tiden. Man slår f.eks. en fair mønt. Den lander på hovedet 10 gange i træk. Du er sikker på, at det næste kast nødvendigvis bliver plat…ikke sandt?
Hvad er chancen for, at den næste mønt igen bliver plat?
Det er stadig 1/2. At slå på en mønt er en uafhængig begivenhed. Med andre ord er resultatet af det næste kast ikke påvirket af det, der er sket tidligere. Det er som om det var første gang, du nogensinde har vendt mønten. Sandsynligheden er uændret.
Hvorfor “føles” det så som om det skulle være plat?
Vi har en tendens til at tænke på begivenhederne samlet i stedet for hver for sig. Selv om sandsynligheden for at kaste plat forbliver den samme for hvert kast, er den samlede chance for at kaste 11 plat i træk lille.
Lad os beregne den.
Vi lærte i den foregående sandsynlighedslektion, at når vi kæder flere hændelser sammen og ønsker, at de alle skal indtræffe (“og”-scenariet), skal vi gange deres sandsynligheder sammen.
Da hvert møntkast har en sandsynlighed for hoveder lig med 1/2, skal jeg blot gange 1/2 sammen elleve gange.
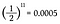
Det er en chance på 0,05 % for at slå elleve hoveder i træk! Men før du ånder lettet ud og siger: “Se, jeg vidste det!”, så lad os beregne chancen for at få en hale i stedet ved det ellevte kast.
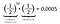
Ja, det er rigtigt. Det er lige så sandsynligt at slå ti hoveder efterfulgt af en hale, som det er at slå elleve hoveder i træk. Faktisk, fordi den individuelle sandsynlighed for at slå hoveder er den samme som sandsynligheden for at slå plat, vil hvert arrangement af 11 møntkast resultere i den samme sandsynlighed på 0,0005. Hvert arrangement er lige sandsynligt.
Så… hvorfor “FØLES” det usandsynligt at slå ti hoveder i træk?
Den almindelige misforståelse skyldes ikke sandsynlighed, men en misforståelse af kombinatorik og permutationer.
Så vidt vi har fastslået, at:
- Sandsynligheden for at slå plat eller krone er lige sandsynlig ved hvert enkelt kast: P(H) = P(T) = 1/2.
- Hvert unikt arrangement (permutation) af mulige møntkast er lige sandsynligt.
Så hvad sker der?
Forståelse af prøveområdet
Prøveområdet er simpelthen en liste over alle de mulige udfaldsarrangementer (permutationer). Da prøveområdet for 11 på hinanden følgende møntkast er ret stort, skal vi i stedet undersøge et enklere tilfælde.
Stikprøverummet for fire møntkast er:

Intuitivt kan vi tænke: Det er mere sandsynligt at slå 2 plat og 2 plat ud af fire kast end kun plat eller kun plat.
Og det er sandt. Lad os regne det ud.
Vi ved, at hver af de seksten permutationer er lige sandsynlige, fordi P(H) = P(T) = 1/2. Så hver permutation har en lige stor sandsynlighed:

Note: Fordi prøveområdet repræsenterer alle mulige udfald, er summen af alle sandsynligheder altid lig med 1 (F.eks. 0,0625 – 16 = 1).
Hvor mange forskellige møntkast-permutationer resulterer i en hvilken som helst kombination 0f 2 plat og 2 krone?

Bemærk, at 6 ud af 16 mulige udfald resulterer i en kombination af to hoved/to hale. Da en hvilken som helst af disse seks permutationer opfylder vores kriterier, betragtes dette som et “eller”-scenarie – så læg sandsynlighederne sammen (eller multiplicer blot med 6, da de alle er ens).
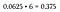
Det er en chance på 37,5 % for at kaste en kombination af 2 hoveder og 2 haler, hvilket er langt større end sandsynligheden for at kaste alle hoveder eller alle haler (som stadig er 6.25% hver, da der kun er én permutation af hver i vores prøveområde).
Det er derfor, vi intuitivt ved, at det er mere sandsynligt at kaste lige mange hoveder og haler end at kaste alle af den ene slags, samtidig med at vi stadig fastholder det faktum, at begivenhederne er uafhængige med individuelle kast og permutationer med lige stor sandsynlighed.
Permutationer &Kombinationer
En stor del af en vellykket beregning af sandsynligheder er at forstå permutationer og kombinationer grundigt. Så det er der, vi skal hen til næste gang!