 Logistisk regression (også kaldet logit-regression eller logit-model) blev udviklet af statistikeren David Cox i 1958 og er en regressionsmodel, hvor responsvariablen Y er kategorisk. Logistisk regression giver os mulighed for at estimere sandsynligheden for et kategorisk svar baseret på en eller flere prædiktorvariable (X). Den gør det muligt at sige, at tilstedeværelsen af en prædiktor øger (eller mindsker) sandsynligheden for et givet resultat med en bestemt procentdel. Denne vejledning dækker det tilfælde, hvor Y er binær – dvs. hvor den kun kan antage to værdier, “0” og “1”, som repræsenterer udfald som f.eks. bestået/ikke bestået, vundet/tabt, levende/død eller rask/syg. Tilfælde, hvor den afhængige variabel har mere end to udfaldskategorier, kan analyseres med multinomial logistisk regression, eller, hvis de flere kategorier er ordnede, med ordinal logistisk regression. Diskriminantanalyse er imidlertid blevet en populær metode til klassifikation af flere klasser, så vores næste tutorial vil fokusere på denne teknik for disse tilfælde.
Logistisk regression (også kaldet logit-regression eller logit-model) blev udviklet af statistikeren David Cox i 1958 og er en regressionsmodel, hvor responsvariablen Y er kategorisk. Logistisk regression giver os mulighed for at estimere sandsynligheden for et kategorisk svar baseret på en eller flere prædiktorvariable (X). Den gør det muligt at sige, at tilstedeværelsen af en prædiktor øger (eller mindsker) sandsynligheden for et givet resultat med en bestemt procentdel. Denne vejledning dækker det tilfælde, hvor Y er binær – dvs. hvor den kun kan antage to værdier, “0” og “1”, som repræsenterer udfald som f.eks. bestået/ikke bestået, vundet/tabt, levende/død eller rask/syg. Tilfælde, hvor den afhængige variabel har mere end to udfaldskategorier, kan analyseres med multinomial logistisk regression, eller, hvis de flere kategorier er ordnede, med ordinal logistisk regression. Diskriminantanalyse er imidlertid blevet en populær metode til klassifikation af flere klasser, så vores næste tutorial vil fokusere på denne teknik for disse tilfælde.
- tl;dr
- Replikationskrav
- Hvorfor logistisk regression
- Forberedelse af vores data
- En simpel logistisk regression
- Vurdering af koefficienter
- Formulering af forudsigelser
- Multipel logistisk regression
- Modelevaluering & Diagnostik
- Goodness-of-Fit
- Likelihood Ratio Test
- Pseudo
- Residualvurdering
- Validering af forudsagte værdier
- Klassifikationsgrad
- Tidligere ressourcer
tl;dr
Denne tutorial tjener som en introduktion til logistisk regression og dækker1:
- Replikationskrav: Hvad du skal bruge for at reproducere analysen i denne vejledning
- Hvorfor logistisk regression: Hvorfor bruge logistisk regression?
- Forberedelse af vores data: Forbered vores data til modellering
- Simpel logistisk regression: Forbered vores data til modellering
- Simpel logistisk regression: Forudsigelse af sandsynligheden for respons Y med en enkelt forudsigelsesvariabel X
- Multipel logistisk regression: Forudsigelse af sandsynligheden for respons Y med en enkelt forudsigelsesvariabel X
- Forudsigelse af sandsynligheden for respons Y med flere prædiktorvariable
- Modelvurdering & diagnostik: Hvor godt passer modellen til dataene? Hvilke prædiktorer er vigtigst? Er forudsigelserne nøjagtige?
Replikationskrav
Denne vejledning udnytter primært Default-dataene, der leveres af ISLR-pakken. Dette er et simuleret datasæt, der indeholder oplysninger om ti tusinde kunder, f.eks. om kunden har misligholdt sine forpligtelser, om kunden er studerende, den gennemsnitlige saldo, som kunden har, og kundens indkomst. Vi vil også bruge et par pakker, der leverer datamanipulation, visualisering, funktioner til pipeline-modellering og funktioner til oprydning af modeloutput.
# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rowsHvorfor logistisk regression
Linær regression er ikke hensigtsmæssig i tilfælde af en kvalitativ respons. Hvorfor ikke? Lad os antage, at vi forsøger at forudsige den medicinske tilstand hos en patient på skadestuen på grundlag af hendes symptomer. I dette forenklede eksempel er der tre mulige diagnoser: slagtilfælde, overdosis af medicin og epileptisk anfald. Vi kunne overveje at kode disse værdier som en kvantitativ responsvariabel, Y , på følgende måde:
Med denne kodning kunne man ved hjælp af mindste kvadrater tilpasse en lineær regressionsmodel for at forudsige Y på grundlag af et sæt prædiktorer . Desværre indebærer denne kodning en rækkefølge af resultaterne, idet overdosis af lægemidler placeres mellem slagtilfælde og epileptisk anfald, og idet man insisterer på, at forskellen mellem slagtilfælde og overdosis af lægemidler er den samme som forskellen mellem overdosis af lægemidler og epileptisk anfald. I praksis er der ingen særlig grund til, at dette skal være tilfældet. Man kunne f.eks. vælge en lige så fornuftig kodning,
som ville indebære et helt andet forhold mellem de tre tilstande. Hver af disse kodninger ville give fundamentalt forskellige lineære modeller, som i sidste ende ville føre til forskellige sæt forudsigelser på testobservationer.
Mere relevant for vores data, hvis vi forsøger at klassificere en kunde som en misligholder med høj vs. lav risiko baseret på hans saldo, kunne vi bruge lineær regression; den venstre figur nedenfor illustrerer imidlertid, hvordan lineær regression ville forudsige sandsynligheden for misligholdelse. Desværre forudsiger vi for saldi tæt på nul en negativ sandsynlighed for misligholdelse; hvis vi skulle forudsige for meget store saldi, ville vi få værdier større end 1. Disse forudsigelser er ikke fornuftige, da den sande sandsynlighed for misligholdelse, uanset kreditkortsaldo, naturligvis skal ligge mellem 0 og 1.
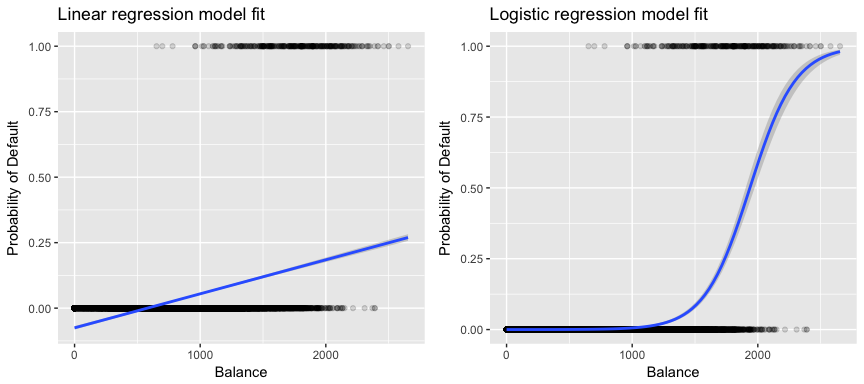
For at undgå dette problem skal vi modellere p(X) ved hjælp af en funktion, der giver output mellem 0 og 1 for alle værdier af X. Mange funktioner lever op til denne beskrivelse. I logistisk regression bruger vi den logistiske funktion, som er defineret i Eq. 1 og illustreret i figuren til højre ovenfor.
Forberedelse af vores data
Som i regressionsvejledningen opdeler vi vores data i et træningssæt (60 %) og et testdatasæt (40 %), så vi kan vurdere, hvor godt vores model klarer sig på et datasæt uden for stikprøven.
set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- defaultEn simpel logistisk regression
Vi vil tilpasse en logistisk regressionsmodel for at forudsige sandsynligheden for, at en kunde misligholder sine forpligtelser, på grundlag af den gennemsnitlige saldo, som kunden har på sig. Funktionen glm tilpasser generaliserede lineære modeller, som er en klasse af modeller, der omfatter logistisk regression. Syntaksen for glm-funktionen svarer til syntaksen for lm, bortset fra at vi skal videregive argumentet family = binomial for at fortælle R, at den skal køre en logistisk regression i stedet for en anden type generaliseret lineær model.
model1 <- glm(default ~ balance, family = "binomial", data = train)I baggrunden bruger glm, maximum likelihood til at tilpasse modellen. Den grundlæggende intuition bag brugen af maximum likelihood til at tilpasse en logistisk regressionsmodel er som følger: Vi søger estimater for og således, at den forudsagte sandsynlighed for misligholdelse for hvert enkelt individ ved hjælp af ligning 1 svarer så tæt som muligt til individets observerede misligholdelsesstatus. Med andre ord forsøger vi at finde og på en sådan måde, at hvis vi indsætter disse estimater i modellen for p(X), som er angivet i ligning 1, får vi et tal tæt på 1 for alle personer, der har misligholdt deres forpligtelser, og et tal tæt på 0 for alle personer, der ikke har misligholdt deres forpligtelser. Denne intuition kan formaliseres ved hjælp af en matematisk ligning, der kaldes en sandsynlighedsfunktion:
Skønnene og vælges således, at de maksimerer denne sandsynlighedsfunktion. Maximum likelihood er en meget generel tilgang, der bruges til at tilpasse mange af de ikke-lineære modeller, som vi vil undersøge i fremtidige tutorials. Det resulterer i en S-formet sandsynlighedskurve, som er illustreret nedenfor (bemærk, at vi skal konvertere vores responsvariabel til en binært kodet variabel for at plotte den logistiske regressionstilpasningslinje).
default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")
Som i forbindelse med lineær regression kan vi vurdere modellen ved hjælp af summary eller glance. Bemærk, at koefficientoutputformatet svarer til det, vi så i lineær regression; detaljerne om god tilpasning i bunden af summary er dog anderledes. Vi vil komme mere ind på dette senere, men bemærk blot, at du ser ordet afvigelse. Devians er analogt med summen af kvadraternes beregninger i lineær regression og er et mål for manglende tilpasning til dataene i en logistisk regressionsmodel. Nul-afvigelsen repræsenterer forskellen mellem en model med kun interceptet (hvilket betyder “ingen prædiktorer”) og en mættet model (en model med en teoretisk perfekt tilpasning). Målet er, at modelafvigelsen (noteret som Residualafvigelse) skal være lavere; mindre værdier indikerer en bedre tilpasning. I denne henseende giver nulmodellen en basislinje, som man kan sammenligne prædiktormodeller på.
summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8Vurdering af koefficienter
Nedenstående tabel viser de koefficientestimater og relaterede oplysninger, der er resultatet af tilpasning af en logistisk regressionsmodel med henblik på at forudsige sandsynligheden for misligholdelse = Ja ved hjælp af saldo. Husk på, at koefficientestimaterne fra logistisk regression karakteriserer forholdet mellem prædiktor- og responsvariablen på en logodds-skala (se kapitel 3 i ISLR1 for yderligere oplysninger). Vi ser således, at ; dette indikerer, at en stigning i saldoen er forbundet med en stigning i sandsynligheden for misligholdelse. For at være præcis er en stigning i saldoen på én enhed forbundet med en stigning i log-oddset for misligholdelse med 0,0057 enheder.
tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82Vi kan yderligere fortolke saldokoefficienten som – for hver dollar stigning i den månedlige saldo, der bæres, stiger oddset for, at kunden misligholder sine forpligtelser, med en faktor 1.0057.
exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00Mange aspekter af koefficientoutputtet svarer til dem, der blev diskuteret i det lineære regressionsoutput. Vi kan f.eks. måle konfidensintervallerne og nøjagtigheden af koefficientestimaterne ved at beregne deres standardfejl. Har f.eks. en p-værdi < 2e-16, hvilket tyder på en statistisk signifikant sammenhæng mellem den medbragte saldo og sandsynligheden for misligholdelse. Vi kan også bruge standardfejlene til at få konfidensintervaller, som vi gjorde i vejledningen om lineær regression:
confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411Formulering af forudsigelser
Når koefficienterne er blevet estimeret, er det en simpel sag at beregne sandsynligheden for misligholdelse for en given kreditkortsaldo. Matematisk set forudsiger vi ved hjælp af koefficientestimaterne fra vores model, at sandsynligheden for misligholdelse for en person med en saldo på 1.000 dollars er mindre end 0,5 %
Vi kan forudsige sandsynligheden for misligholdelse i R ved hjælp af funktionen predict (sørg for at inkludere type = "response"). Her sammenligner vi sandsynligheden for misligholdelse på grundlag af saldi på 1 000 $ og 2 000 $. Som du kan se, stiger sandsynligheden for misligholdelse markant fra 0,5 % til 58 %, når saldoen bevæger sig fra 1000 $ til 2000 $!
predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269Man kan også bruge kvalitative prædiktorer med den logistiske regressionsmodel. Som eksempel kan vi tilpasse en model, der bruger variablen student.
model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511Den koefficient, der er knyttet til student = Yes, er positiv, og den tilhørende p-værdi er statistisk signifikant. Dette indikerer, at studerende har en tendens til at have højere sandsynlighed for misligholdelse end ikke-studerende. Faktisk tyder denne model på, at en studerende har næsten dobbelt så stor sandsynlighed for misligholdelse som ikke-studerende. I næste afsnit vil vi dog se hvorfor.
predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019Multipel logistisk regression
Vi kan også udvide vores model, som det ses i Eq. 1, så vi kan forudsige et binært svar ved hjælp af flere prædiktorer, hvor er p prædiktorer:
Lad os gå videre og tilpasse en model, der forudsiger sandsynligheden for misligholdelse baseret på variablerne saldo, indkomst (i tusinde kroner) og studiestatus. Der er et overraskende resultat her. De p-værdier, der er forbundet med saldo og student=Yes-status, er meget små, hvilket indikerer, at hver af disse variabler er forbundet med sandsynligheden for misligholdelse. Koefficienten for variablen studerende er imidlertid negativ, hvilket indikerer, at studerende er mindre tilbøjelige til at misligholde deres forpligtelser end ikke-studerende. I modsætning hertil viser koefficienten for den studerendes variabel i model 2, hvor vi forudsagde sandsynligheden for misligholdelse udelukkende på grundlag af status som studerende, at studerende har en større sandsynlighed for misligholdelse. Hvad giver?
model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03Det højre panel i figuren nedenfor giver en forklaring på denne uoverensstemmelse. Variablerne studerende og saldo er korreleret. Studerende har en tendens til at have en højere gæld, hvilket igen er forbundet med en højere sandsynlighed for misligholdelse. Med andre ord er studerende mere tilbøjelige til at have store kreditkortsaldi, der, som vi ved fra det venstre panel i nedenstående figur, har tendens til at være forbundet med høje misligholdelsesprocenter. Selv om en individuel studerende med en given kreditkortsaldo vil have en lavere sandsynlighed for misligholdelse end en ikke-studerende med den samme kreditkortsaldo, betyder det faktum, at studerende som helhed har tendens til at have højere kreditkortsaldi, at studerende samlet set har tendens til at misligholde deres forpligtelser i højere grad end ikke-studerende. Dette er en vigtig sondring for et kreditkortselskab, der forsøger at afgøre, hvem de skal tilbyde kredit til. En studerende er mere risikabel end en ikke-studerende, hvis der ikke foreligger oplysninger om den studerendes kreditkortsaldo. Den studerende er imidlertid mindre risikabel end en ikke-studerende med den samme kreditkortsaldo!
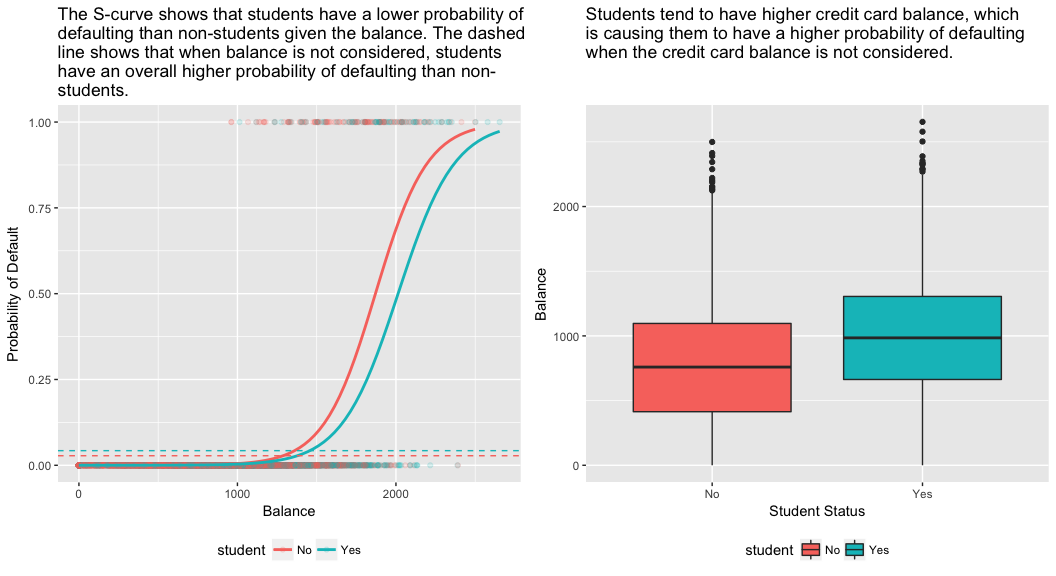
Dette enkle eksempel illustrerer de farer og finesser, der er forbundet med at udføre regressioner, som kun omfatter en enkelt prædiktor, når andre prædiktorer også kan være relevante. De resultater, der opnås ved hjælp af én prædiktor, kan være helt forskellige fra dem, der opnås ved hjælp af flere prædiktorer, især når der er korrelation mellem prædiktorerne. Dette fænomen er kendt som confounding.
I tilfælde af flere prædiktorvariabler ønsker vi nogle gange at forstå, hvilken variabel der har størst indflydelse på forudsigelsen af responsvariablen (Y). Det kan vi gøre med varImp fra pakken caret. Her ser vi, at balance er den vigtigste med stor margen, mens studenterstatus er mindre vigtig efterfulgt af indkomst (som alligevel viste sig at være insignifikant (p = .64)).
caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947Som tidligere kan vi nemt lave forudsigelser med denne model. For eksempel har en studerende med en kreditkortsaldo på 1.500 dollars og en indkomst på 40.000 dollars en estimeret sandsynlighed for misligholdelse på
En ikke-studerende med samme saldo og indkomst har en estimeret sandsynlighed for misligholdelse på
new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288Sådan ser vi, at for den givne saldo og indkomst (selv om indkomsten er insignifikant) har en studerende omkring halvt så stor sandsynlighed for misligholdelse som en ikke-studerende.
Modelevaluering & Diagnostik
Der er indtil videre bygget tre logistiske regressionsmodeller, og koefficienterne er blevet undersøgt. Der er dog stadig nogle kritiske spørgsmål tilbage. Er modellerne egnede? Hvor godt passer modellen til dataene? Og hvor nøjagtige er forudsigelserne på et datasæt uden for stikprøven?
Goodness-of-Fit
I vejledningen om lineær regression så vi, hvordan F-statistik, og justeret , og residualdiagnostik informerer os om, hvor godt modellen passer til dataene. Her vil vi se på et par måder at vurdere goodness-of-fit for vores logit-modeller på.
Likelihood Ratio Test
Først kan vi bruge en Likelihood Ratio Test til at vurdere, om vores modeller forbedrer tilpasningen. Tilføjelse af prædiktorvariabler til en model vil næsten altid forbedre modellens tilpasning (dvs. øge den logiske sandsynlighed og reducere modellens afvigelse i forhold til nulafvigelsen), men det er nødvendigt at teste, om den observerede forskel i modellens tilpasning er statistisk signifikant. Vi kan bruge anova til at udføre denne test. Resultaterne viser, at sammenlignet med model1 reducerer model3 residualafvigelsen med over 13 (husk, at et mål med logistisk regression er at finde en model, der minimerer residualafvigelserne). Endnu vigtigere er det, at denne forbedring er statistisk signifikant ved p = 0,001. Dette tyder på, at model3 giver en bedre tilpasning af modellen.
anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Pseudo
I modsætning til lineær regression med almindelig mindste kvadraters estimation er der ingen statistik, der forklarer, hvor stor en del af variansen i den afhængige variabel der forklares af prædiktorerne. Der findes dog en række pseudo-metrikker, som kan være af værdi. Den mest bemærkelsesværdige er McFadden’s , som er defineret som
hvor er loglikelihood-værdien for den tilpassede model og er loglikelihood-værdien for nulmodellen med kun et intercept som en prædiktor. Målingen varierer fra 0 til lige under 1, idet værdier tættere på nul angiver, at modellen ikke har nogen forudsigelseskraft. I modsætning til lineær regression opnår modellerne dog sjældent en høj McFadden . Faktisk repræsenterer modeller med et McFadden-pseudo ifølge McFadden selv en meget god tilpasning. Vi kan vurdere McFaddens pseudoværdier for vores modeller med:
list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543Vi ser, at model 2 har en meget lav værdi, hvilket bekræfter dens dårlige tilpasning. Model 1 og 3 har imidlertid meget højere værdier, hvilket tyder på, at de forklarer en rimelig stor del af variansen i standarddataene. Desuden ser vi, at model 3 kun forbedrer den så småt.
Residualvurdering
Hold dig for øje, at logistisk regression ikke antager, at residualerne er normalfordelte eller at variansen er konstant. Afvigelsesresidualet er imidlertid nyttigt til at afgøre, om enkelte punkter ikke passer godt til modellen. Her kan vi tilpasse de standardiserede deviance-residualer for at se, hvor mange der overstiger 3 standardafvigelser. Først uddrager vi flere nyttige dele af modelresultaterne med augment og fortsætter derefter med at plotte.
model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)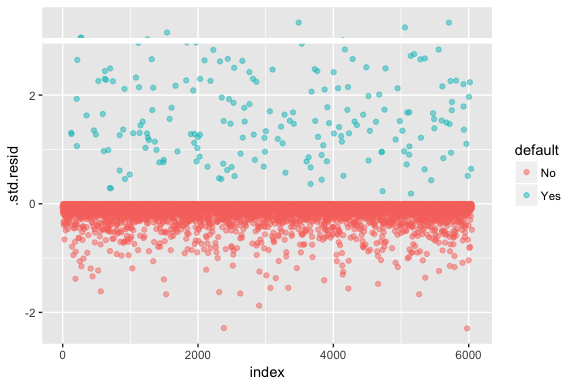
Disse standardiserede residualer, der overstiger 3, repræsenterer mulige outliers og fortjener måske nærmere opmærksomhed. Vi kan filtrere efter disse residualer for at få et nærmere kig. Vi ser, at alle disse observationer repræsenterer kunder, der misligholder med budgetter, der er meget lavere end de normale misligholdere.
model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709I lighed med lineær regression kan vi også identificere indflydelsesrige observationer med Cook’s afstandsværdier. Her identificerer vi de 5 største værdier.
plot(model1, which = 4, id.n = 5)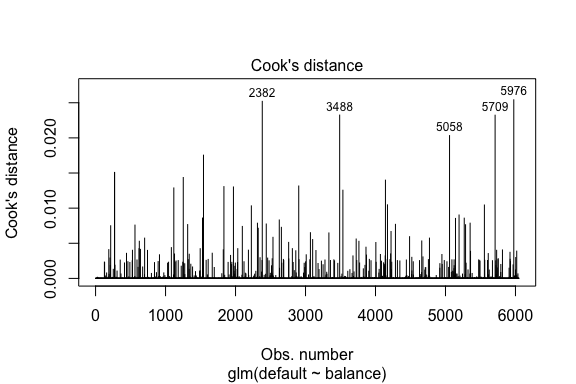
Og vi kan også undersøge disse yderligere. Her ser vi, at de fem mest indflydelsesrige punkter omfatter:
- de kunder, der misligholdte med meget lave saldi, og
- to kunder, der ikke misligholdte, men som alligevel havde saldi på over 2.000 $
Det betyder, at hvis vi fjerner disse observationer (hvilket ikke anbefales), vil formen, placeringen og konfidensintervallet for vores S-kurve for logistisk regression sandsynligvis ændre sig.
model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976Validering af forudsagte værdier
Klassifikationsgrad
Når man udvikler modeller til forudsigelse, er den mest kritiske måleenhed vedrørende hvor godt modellen klarer sig med hensyn til at forudsige målvariablen på observationer uden for stikprøven. Først skal vi bruge de estimerede modeller til at forudsige værdier på vores træningsdatasæt (train). Når du bruger predict, skal du sørge for at medtage type = response, så forudsigelsen returnerer sandsynligheden for misligholdelse.
test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")Nu kan vi sammenligne den forudsagte målvariabel med de observerede værdier for hver model og se, hvilken model der klarer sig bedst. Vi kan starte med at bruge forvirringsmatrixen, som er en tabel, der beskriver klassifikationspræstationen for hver model på testdataene. Hver kvadrant i tabellen har en vigtig betydning. I dette tilfælde repræsenterer “Nej” og “Ja” i rækkerne, om kunderne har misligholdt deres forpligtelser eller ej. “FALSK” og “SANDT” i kolonnerne repræsenterer, om vi forudsagde, at kunderne ville misligholde deres forpligtelser eller ej.
- sande positive (kvadrant nederst til højre): Dette er tilfælde, hvor vi forudsagde, at kunden ville misligholde sine forpligtelser, og det gjorde de.
- sande negative (kvadrant øverst til venstre): Vi forudsagde ingen misligholdelse, og kunden misligholdte ikke.
- falsk positive tilfælde (øverste højre kvadrant): Vi forudsagde ja, men kunden misligholdte faktisk ikke sine forpligtelser. (Også kendt som en “type I-fejl”.)
- falsk negative (nederste venstre kvadrant): Vi forudsagde nej, men de misligholdte faktisk. (Også kendt som en “type II-fejl.”)
Resultaterne viser, at model1 og model3 er meget ens. 96 % af de forudsagte observationer er sande negative og ca. 1 % er sande positive. Begge modeller har en type II-fejl på mindre end 3 %, hvor modellen forudsiger, at kunden ikke vil misligholde sine forpligtelser, men det gjorde de faktisk. Og begge modeller har en type I-fejl på under 1 %, hvor modellerne forudsiger, at kunden vil misligholde sine forpligtelser, men aldrig har gjort det. model2 resultaterne er markant forskellige; denne model forudsiger præcist de kunder, der ikke misligholder deres forpligtelser (et resultat af, at 97 % af dataene er ikke-misligholdere), men forudsiger faktisk aldrig de kunder, der misligholder deres forpligtelser!
list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009Vi ønsker også at forstå missclassifikations- (aka fejl-)satser (eller vi kunne vende dette om til nøjagtighedssatser). Vi ser ikke meget forbedring mellem model 1 og 3, og selv om model 2 har en lav fejlprocent, skal du ikke glemme, at den aldrig præcist forudsiger kunder, der rent faktisk misligholder.
test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994Vi kan få yderligere indsigt ved at se på de rå værdier (ikke procenter) i vores forvirringsmatrix. Lad os se på model 1 for at illustrere det. Vi kan se, at der er i alt kunder, der har misligholdt deres forpligtelser. Af de samlede misligholdelser blev ikke forudsagt. Alternativt kan vi sige, at kun en del af misligholdelsesforekomsterne blev forudsagt – dette er kendt som modellens præcision (også kaldet følsomhed). Så selv om den samlede fejlprocent er lav, er præcisionen også lav, hvilket ikke er godt!
table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40Med klassifikationsmodeller vil man også her bruge udtrykkene sensitivitet og specificitet, når man karakteriserer modellens ydeevne. Som nævnt ovenfor er sensitivitet synonymt med præcision. Specificiteten er imidlertid den procentdel af ikke-defaulters, der identificeres korrekt, her (nøjagtigheden her er i høj grad drevet af, at 97 % af observationerne i vores data er ikke-defaulters). Betydningen mellem følsomhed og specificitet er afhængig af konteksten. I dette tilfælde vil et kreditkortselskab sandsynligvis være mere optaget af følsomhed, da de ønsker at reducere deres risiko. Derfor er de måske mere optaget af at indstille en model, så deres sensitivitet/præcision forbedres.
Den modtagende operationelle karakteristik (ROC) er et visuelt mål for klassificeringspræstationens ydeevne. Ved hjælp af andelen af positive datapunkter, der korrekt betragtes som positive, og andelen af negative datapunkter, der fejlagtigt betragtes som positive, genererer vi en grafisk fremstilling, der viser afvejningen mellem den hastighed, hvormed man kan forudsige noget korrekt, og den hastighed, hvormed man fejlagtigt forudsiger noget. I sidste ende er vi optaget af arealet under ROC-kurven, eller AUC. Denne måleenhed varierer fra 0,50 til 1,00, og værdier over 0,80 indikerer, at modellen gør et godt stykke arbejde med at skelne mellem de to kategorier, som omfatter vores målvariabel. Vi kan sammenligne ROC- og AUC-værdierne for model 1 og 2, som viser en stærk forskel i præstation. Vi ønsker helt klart, at vores ROC-plots skal se mere ud som model 1’s (venstre) end model 2’s (højre)!
library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()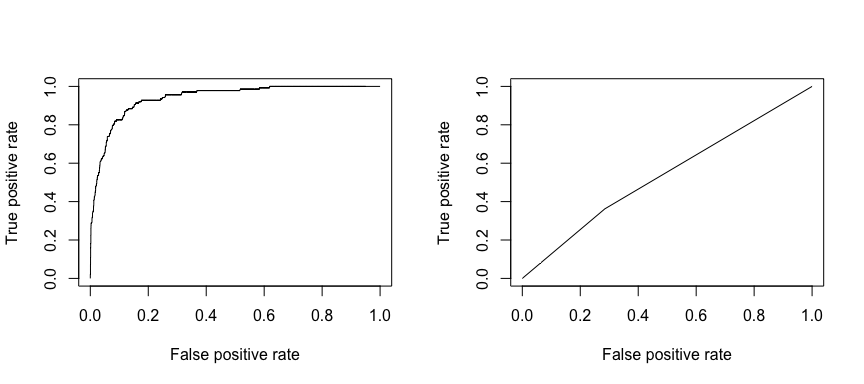
Og for at beregne AUC numerisk kan vi bruge følgende. Husk, at AUC vil ligge mellem 0,50 – 1,00. Således er model 2 en meget dårlig klassificeringsmodel, mens model 1 er en meget god klassificeringsmodel.
# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955Vi kan fortsætte med at “tune” vores modeller for at forbedre disse klassificeringssatser. Hvis du kan forbedre dine AUC- og ROC-kurver (hvilket betyder, at du forbedrer klassifikationsnøjagtighedssatserne), skaber du et “løft”, hvilket betyder, at du løfter klassifikationsnøjagtigheden.
Tidligere ressourcer
Dette vil få dig godt i gang med logistisk regression. Husk, at der er meget mere, du kan grave i, så de følgende ressourcer vil hjælpe dig med at lære mere:
- An Introduction to Statistical Learning
- Applied Predictive Modeling
- Elements of Statistical Learning
-
Denne vejledning blev bygget som et supplement til kapitel 4, afsnit 3 i An Introduction to Statistical Learning 2