Das Aufbauprinzip
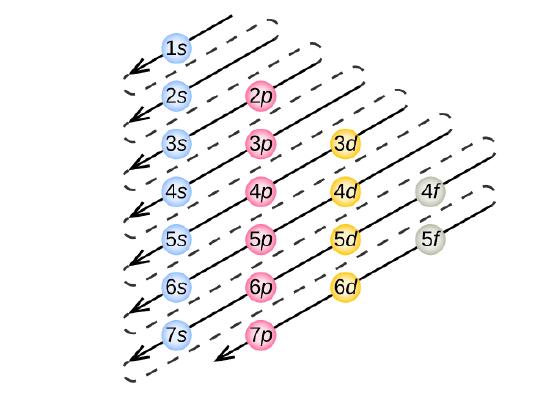
Um die Elektronenkonfiguration für ein bestimmtes Atom zu bestimmen, können wir die Strukturen in der Reihenfolge der Ordnungszahlen „aufbauen“. Beginnend mit Wasserstoff und weiter über die Perioden des Periodensystems, fügen wir jeweils ein Proton zum Kern und ein Elektron zur entsprechenden Unterschale hinzu, bis wir die Elektronenkonfigurationen aller Elemente beschrieben haben. Dieses Verfahren wird als Aufbau-Prinzip bezeichnet, abgeleitet vom deutschen Wort Aufbau. Jedes hinzugefügte Elektron nimmt die Unterschale mit der niedrigsten verfügbaren Energie ein (in der in Abbildung \(\PageIndex{3}\)), vorbehaltlich der Beschränkungen durch die zulässigen Quantenzahlen gemäß dem Pauli-Ausschlussprinzip. Die Elektronen treten in die Unterschalen mit höherer Energie erst ein, nachdem die Unterschalen mit niedrigerer Energie bis zur Kapazität gefüllt worden sind. Abbildung \(\PageIndex{3}\) veranschaulicht die traditionelle Art und Weise, sich die Füllreihenfolge für Atomorbitale zu merken.
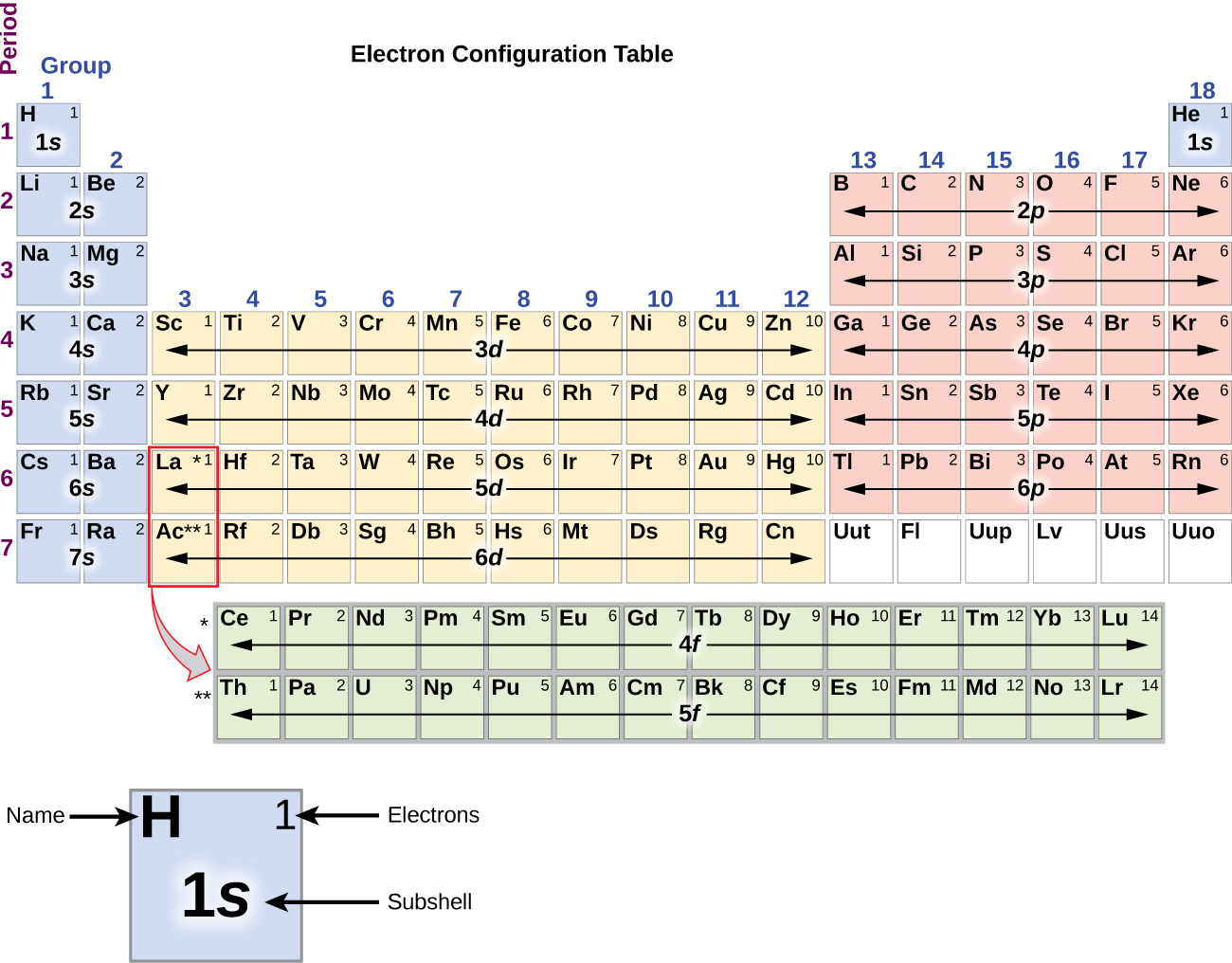
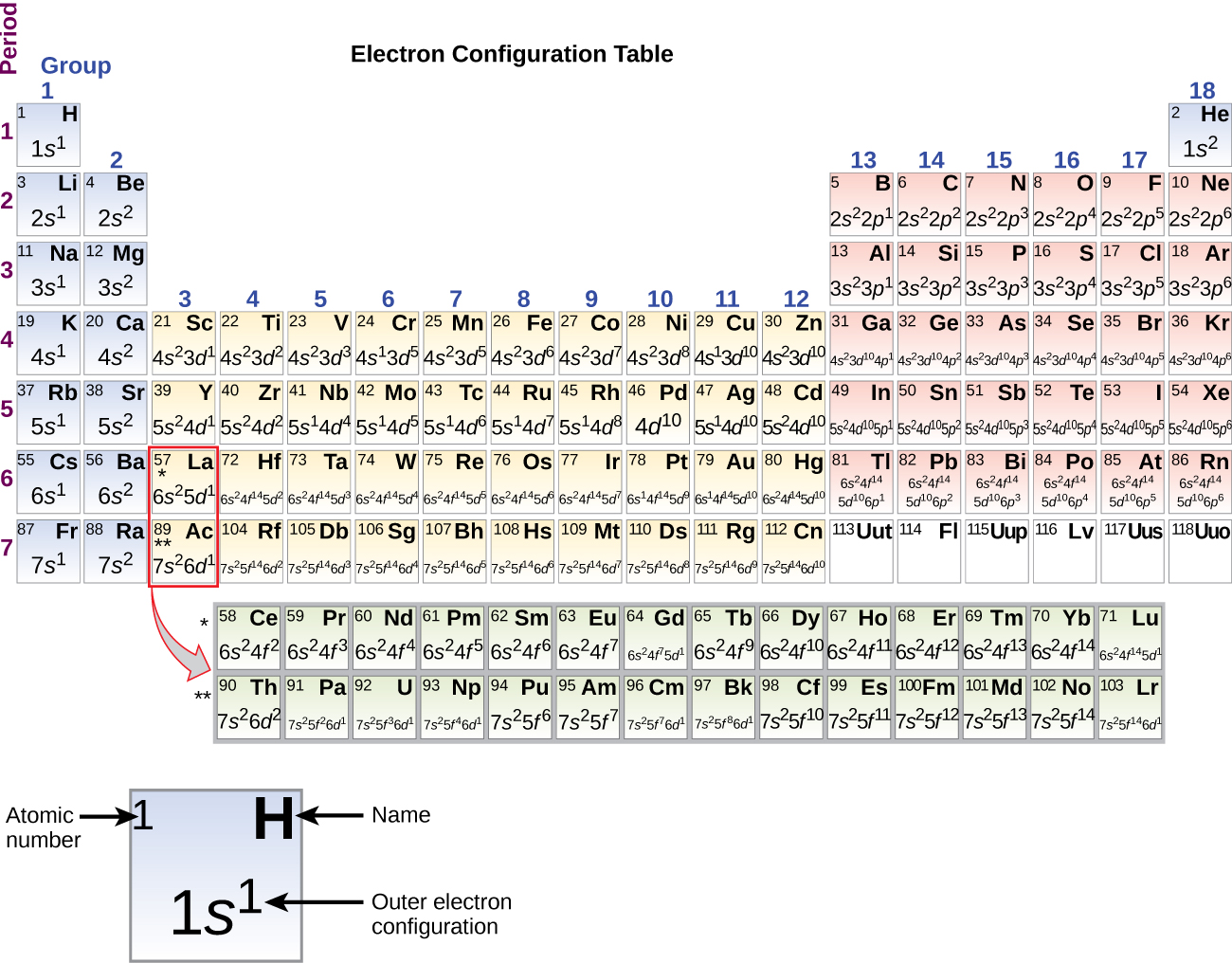
Da die Anordnung des Periodensystems auf den Elektronenkonfigurationen beruht, bietet Abbildung \(\PageIndex{4}\) eine alternative Methode zur Bestimmung der Elektronenkonfiguration. Die Auffüllreihenfolge beginnt einfach bei Wasserstoff und umfasst jede Unterschale in aufsteigender Z-Reihenfolge. Nach dem Auffüllen des 3p-Blocks bis zu Ar sehen wir zum Beispiel, dass das Orbital 4s (K, Ca) ist, gefolgt von den 3d-Orbitalen.
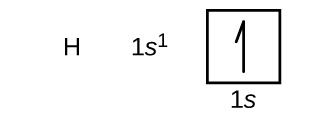
Wir werden nun die Grundzustandselektronenkonfiguration und das Orbitaldiagramm für eine Auswahl von Atomen in der ersten und zweiten Periode des Periodensystems konstruieren. Orbitaldiagramme sind bildliche Darstellungen der Elektronenkonfiguration, die die einzelnen Orbitale und die Paarungsanordnung der Elektronen zeigen. Wir beginnen mit einem einzelnen Wasserstoffatom (Ordnungszahl 1), das aus einem Proton und einem Elektron besteht. Bezieht man sich auf die Abbildung \(\PageIndex{3}\) oder \(\PageIndex{4}\), würde man erwarten, dass sich das Elektron im 1s-Orbital befindet. Der Konvention entsprechend wird der Wert \(m_s=+\dfrac{1}{2}\) in der Regel zuerst ausgefüllt. Die Elektronenkonfiguration und das Orbitaldiagramm lauten:
Nach Wasserstoff folgt das Edelgas Helium, das die Ordnungszahl 2 hat. Das Heliumatom enthält zwei Protonen und zwei Elektronen. Das erste Elektron hat die gleichen vier Quantenzahlen wie das Elektron des Wasserstoffatoms (n = 1, l = 0, ml = 0, \(m_s=+\dfrac{1}{2}\)). Das zweite Elektron geht ebenfalls in das 1s-Orbital und füllt dieses Orbital auf. Das zweite Elektron hat die gleichen n-, l- und ml-Quantenzahlen, muss aber die entgegengesetzte Spin-Quantenzahl haben, \(m_s=-\dfrac{1}{2}\). Dies steht im Einklang mit dem Pauli-Ausschlussprinzip: Keine zwei Elektronen im selben Atom können denselben Satz von vier Quantenzahlen haben. Für Orbitaldiagramme bedeutet dies, dass in jedem Kästchen zwei Pfeile stehen (für zwei Elektronen in jedem Orbital) und die Pfeile in entgegengesetzte Richtungen zeigen müssen (für gepaarte Spins). Die Elektronenkonfiguration und das Orbitaldiagramm von Helium lauten:
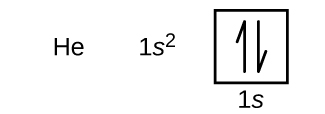
Die n = 1-Schale ist bei einem Heliumatom vollständig gefüllt.
Das nächste Atom ist das Alkalimetall Lithium mit der Ordnungszahl 3. Die ersten beiden Elektronen in Lithium besetzen das 1s-Orbital und haben dieselbe Menge von vier Quantenzahlen wie die beiden Elektronen in Helium. Das verbleibende Elektron muss das Orbital mit der nächst niedrigeren Energie, das 2s-Orbital, besetzen (Abbildung \(\PageIndex{3}\) oder \(\PageIndex{4}\)). Die Elektronenkonfiguration und das Orbitaldiagramm von Lithium lauten also:
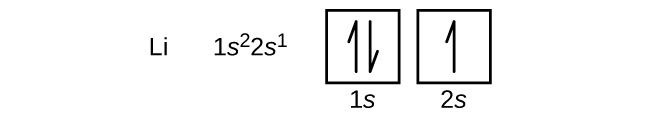
Ein Atom des Erdalkalimetalls Beryllium mit der Ordnungszahl 4 enthält vier Protonen im Kern und vier Elektronen, die den Kern umgeben. Das vierte Elektron füllt den verbleibenden Platz im 2s-Orbital.
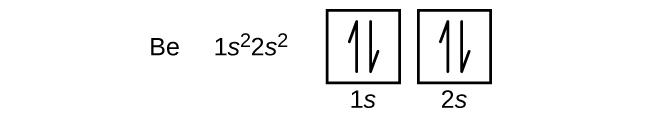
Ein Atom des Bors (Ordnungszahl 5) enthält fünf Elektronen. Die n = 1-Schale ist mit zwei Elektronen besetzt und drei Elektronen besetzen die n = 2-Schale. Da jede s-Unterschale nur zwei Elektronen enthalten kann, muss das fünfte Elektron das nächste Energieniveau besetzen, das ein 2p-Orbital ist. Es gibt drei entartete 2p-Orbitale (ml = -1, 0, +1), und das Elektron kann ein beliebiges dieser p-Orbitale besetzen. Beim Zeichnen von Orbitaldiagrammen werden leere Kästchen eingefügt, um alle leeren Orbitale in der gleichen Unterschale darzustellen, die wir füllen.

Kohlenstoff (Ordnungszahl 6) hat sechs Elektronen. Vier davon besetzen die 1s und 2s Orbitale. Die restlichen zwei Elektronen besetzen die 2p-Unterschale. Wir haben nun die Wahl, eines der 2p-Orbitale zu füllen und die Elektronen zu paaren oder die Elektronen ungepaart in zwei verschiedenen, aber entarteten p-Orbitalen zu belassen. Die Orbitale werden gemäß der Hund’schen Regel gefüllt: Die Konfiguration mit der niedrigsten Energie für ein Atom mit Elektronen innerhalb eines Satzes entarteter Orbitale ist diejenige, die die maximale Anzahl ungepaarter Elektronen aufweist. So haben die beiden Elektronen in den 2p-Orbitalen des Kohlenstoffs identische n-, l- und ms-Quantenzahlen und unterscheiden sich in ihrer ml-Quantenzahl (gemäß dem Pauli-Ausschlussprinzip). Die Elektronenkonfiguration und das Orbitaldiagramm für Kohlenstoff lauten:

Stickstoff (Ordnungszahl 7) füllt die 1s und 2s Unterschalen und hat gemäß der Hund’schen Regel ein Elektron in jedem der drei 2p Orbitale. Diese drei Elektronen haben ungepaarte Spins. Sauerstoff (Ordnungszahl 8) hat ein Elektronenpaar in einem der 2p-Orbitale (die Elektronen haben entgegengesetzte Spins) und ein einzelnes Elektron in jedem der beiden anderen. Fluor (Ordnungszahl 9) hat nur ein 2p-Orbital, das ein ungepaartes Elektron enthält. Beim Edelgas Neon (Ordnungszahl 10) sind alle Elektronen gepaart, und alle Orbitale in den Schalen n = 1 und n = 2 sind gefüllt. Die Elektronenkonfigurationen und Orbitaldiagramme dieser vier Elemente sind:
Das Alkalimetall Natrium (Ordnungszahl 11) hat ein Elektron mehr als das Neonatom. Dieses Elektron muss in die energieärmste verfügbare Unterschale, das 3s-Orbital, gehen, was eine 1s22s22p63s1-Konfiguration ergibt. Die Elektronen, die das/die äußerste(n) Schalenorbital(e) besetzen (höchster Wert von n), werden als Valenzelektronen bezeichnet, während die Elektronen, die die inneren Schalenorbitale besetzen, als Kernelektronen bezeichnet werden ( Abbildung \PageIndex5\PageIndex5). Da die Kernelektronenschalen den Edelgas-Elektronenkonfigurationen entsprechen, können wir die Elektronenkonfigurationen abkürzen, indem wir das Edelgas, das der Kernelektronenkonfiguration entspricht, zusammen mit den Valenzelektronen in einer komprimierten Form schreiben. Für unser Natrium-Beispiel steht das Symbol für die Kernelektronen (1s22s22p6) und unsere abgekürzte oder kondensierte Konfiguration ist 3s1.

In ähnlicher Weise kann die verkürzte Konfiguration von Lithium als 2s1 dargestellt werden, wobei die Konfiguration des Heliumatoms mit der der gefüllten inneren Schale von Lithium identisch ist. Diese Schreibweise der Konfigurationen unterstreicht die Ähnlichkeit der Konfigurationen von Lithium und Natrium. Beide Atome, die zur Familie der Alkalimetalle gehören, haben nur ein Elektron in einer s-Valenzunterschale außerhalb einer gefüllten inneren Schale.
Das Erdalkalimetall Magnesium (Ordnungszahl 12) mit seinen 12 Elektronen in einer 3s2-Konfiguration ist analog zu seinem Familienmitglied Beryllium, 2s2. Beide Atome haben eine gefüllte s-Unterschale außerhalb ihrer gefüllten inneren Schalen. Aluminium (Ordnungszahl 13), mit 13 Elektronen und der Elektronenkonfiguration 3s23p1, ist analog zu seinem Familienmitglied Bor, 2s22p1.
Die Elektronenkonfigurationen von Silizium (14 Elektronen), Phosphor (15 Elektronen), Schwefel (16 Elektronen), Chlor (17 Elektronen) und Argon (18 Elektronen) sind in den Elektronenkonfigurationen ihrer Außenschalen analog zu den entsprechenden Familienmitgliedern Kohlenstoff, Stickstoff, Sauerstoff, Fluor und Neon, außer dass die Hauptquantenzahl der Außenschale der schwereren Elemente um eins auf n = 3 erhöht wurde. Abbildung \(\PageIndex{6}\) zeigt die Elektronenkonfiguration mit der niedrigsten Energie oder im Grundzustand für diese Elemente sowie für die Atome aller bekannten Elemente.
Wenn wir zum nächsten Element im Periodensystem, dem Alkalimetall Kalium (Ordnungszahl 19), kommen, könnten wir erwarten, dass wir beginnen, Elektronen zur 3d-Unterschale hinzuzufügen. Alle verfügbaren chemischen und physikalischen Beweise deuten jedoch darauf hin, dass Kalium wie Lithium und Natrium ist und dass das nächste Elektron nicht dem 3d-Niveau hinzugefügt wird, sondern stattdessen dem 4s-Niveau (Abbildung \(\PageIndex{3}\) oder \(\PageIndex{4}\)). Wie bereits erwähnt, hat das 3d-Orbital ohne radiale Knoten eine höhere Energie, da es weniger durchdringend und stärker vom Kern abgeschirmt ist als das 4s-Orbital, das drei radiale Knoten hat. Kalium hat also eine Elektronenkonfiguration von 4s1. Damit entspricht Kalium in seiner Valenzschalenkonfiguration dem Li und dem Na. Das nächste Elektron wird hinzugefügt, um die 4s-Unterschale zu vervollständigen, und Kalzium hat eine Elektronenkonfiguration von 4s2. Damit hat Calcium eine Elektronenkonfiguration der äußeren Schale, die der von Beryllium und Magnesium entspricht.
Beginnend mit dem Übergangsmetall Scandium (Ordnungszahl 21) werden sukzessive weitere Elektronen in die 3d-Unterschale aufgenommen. Diese Unterschale wird bis zu ihrer Kapazität mit 10 Elektronen aufgefüllt (man bedenke, dass es für l = 2 2l + 1 = 5 Werte von ml gibt, was bedeutet, dass es fünf d-Orbitale gibt, die zusammen eine Kapazität von 10 Elektronen haben). Die 4p-Unterschale füllt sich als nächstes. Man beachte, dass bei drei Serien von Elementen, Scandium (Sc) bis Kupfer (Cu), Yttrium (Y) bis Silber (Ag) und Lutetium (Lu) bis Gold (Au), insgesamt 10 d-Elektronen nacheinander zur (n – 1)-Schale neben der n-Schale hinzugefügt werden, um diese (n – 1)-Schale von 8 auf 18 Elektronen zu bringen. Bei zwei Serien, Lanthan (La) bis Lutetium (Lu) und Actinium (Ac) bis Lawrencium (Lr), werden 14 f-Elektronen (l = 3, 2l + 1 = 7 ml-Werte; also sieben Orbitale mit einer Gesamtkapazität von 14 Elektronen) nacheinander zur (n – 2)-Schale hinzugefügt, um diese Schale von 18 Elektronen auf insgesamt 32 Elektronen zu bringen.
Beispiel \(\PageIndex{1}\): Quantenzahlen und Elektronenkonfigurationen
Wie lautet die Elektronenkonfiguration und das Orbitaldiagramm für ein Phosphoratom? Wie lauten die vier Quantenzahlen für das letzte hinzugefügte Elektron?
Lösung
Die Ordnungszahl von Phosphor ist 15. Ein Phosphoratom enthält also 15 Elektronen. Die Reihenfolge der Besetzung der Energieniveaus ist 1s, 2s, 2p, 3s, 3p, 4s, . . . Die 15 Elektronen des Phosphoratoms füllen sich bis zum 3p-Orbital, das drei Elektronen enthält:
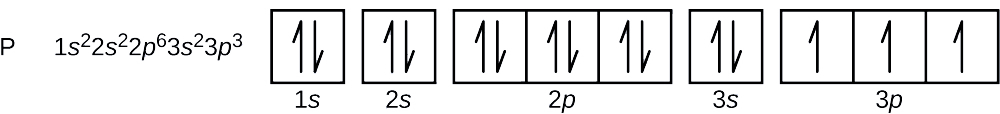
Das letzte hinzugefügte Elektron ist ein 3p-Elektron. Daher ist n = 3 und für ein p-Orbital ist l = 1. Der ml-Wert könnte -1, 0 oder +1 sein. Die drei p-Orbitale sind entartet, so dass jeder dieser ml-Werte korrekt ist. Für ungepaarte Elektronen weist die Konvention den Wert \(+\dfrac{1}{2}\) für die Spinquantenzahl zu; somit ist \(m_s=+\dfrac{1}{2}\).
Übung \(\PageIndex{1}\)
Identifizieren Sie die Atome anhand der gegebenen Elektronenkonfigurationen:
- 4s23d5
- 5s24d105p6
Antwort a
Mn
Antwort b
Xe
Das Periodensystem kann ein leistungsfähiges Werkzeug sein, um die Elektronenkonfiguration eines Elements vorherzusagen. Es gibt jedoch Ausnahmen von der Reihenfolge der Besetzung der Orbitale, die in Abbildung \(\PageIndex{3}\) oder \(\PageIndex{4}\) dargestellt sind. So sind beispielsweise die Elektronenkonfigurationen der Übergangsmetalle Chrom (Cr; Ordnungszahl 24) und Kupfer (Cu; Ordnungszahl 29) nicht die, die wir erwarten würden. Im Allgemeinen handelt es sich bei solchen Ausnahmen um Unterschalen mit sehr ähnlicher Energie, und kleine Effekte können zu Änderungen in der Reihenfolge der Füllung führen.
Im Fall von Cr und Cu stellen wir fest, dass halbgefüllte und vollständig gefüllte Unterschalen offenbar Bedingungen bevorzugter Stabilität darstellen. Diese Stabilität ist so beschaffen, dass ein Elektron vom 4s-Orbital in das 3d-Orbital wechselt, um die zusätzliche Stabilität einer halbgefüllten 3d-Unterschale (in Cr) oder einer gefüllten 3d-Unterschale (in Cu) zu gewinnen. Es gibt auch andere Ausnahmen. So wird beispielsweise für Niob (Nb, Ordnungszahl 41) die Elektronenkonfiguration 5s24d3 vorhergesagt. Experimentell wurde festgestellt, dass seine Grundzustandselektronenkonfiguration tatsächlich 5s14d4 ist. Diese Beobachtung lässt sich damit erklären, dass die Abstoßung der Elektronen bei der Paarung der Elektronen im 5s-Orbital größer ist als die Energielücke zwischen dem 5s-Orbital und dem 4d-Orbital. Es gibt keine einfache Methode, um die Ausnahmen für Atome vorherzusagen, bei denen die Größe der Abstoßungen zwischen den Elektronen größer ist als die geringen Energieunterschiede zwischen den Unterschalen.