Fläche eines unregelmäßigen Polygons

Dieser Artikel beschreibt eine einfache Lösung für ein geometrisches Problem, das ich im Internet auf allzu komplexe Weise beschrieben finde. Das Problem besteht darin, den Flächeninhalt und die Umfangslänge einer zweidimensionalen, geschlossenen Figur wie dem Grundriss eines Zimmers, eines Grundstücks oder einer beliebigen anderen zweidimensionalen, begrenzten Figur (eines „unregelmäßigen Polygons“) zu berechnen, unabhängig davon, wie komplex sie ist.

Ich erhebe sicherlich keinen Anspruch auf Originalität für diese Methode. Versionen gibt es seit der Zeit von Gauß oder davor. Aber die meisten Online-Artikel beschreiben die Methode auf unnötig komplexe Weise. Zu den Referenzen gehören der Wikipedia-Artikel über die Schnürsenkelformel, eine ähnlich komplexe Methode im Polygon-Artikel und eine Reihe von Artikeln, die eher darauf abzielen, die Gelehrsamkeit des Autors zu demonstrieren, als eine möglichst komplexe Darstellung der Methode zu liefern. Dieser Artikel (PDF) zeigt einen der am wenigsten komplexen (aber keineswegs einfachen) Ausdrücke:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\ \end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\\ y_1 & y_2\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\\ y_2 & y_3\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\ y_{n-2} & y_{n-1}\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\\ y_{n-1} & y_0\\ \end{array} \right| \right\}$

Dabei ist $x_n,y_n$ ein in kartesischen Koordinaten ausgedrückter Polygonpunkt, und $\left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\ \end{array} \right|$ bezieht sich auf eine Determinante mit dem Wert $x_0 \mal y_1 – y_0 \mal x_1$

Lassen Sie sich von der obigen Darstellung nicht entmutigen – die Anwendung dieser Methode ist einfacher als das Verständnis ihrer mathematischen Grundlagen. Bei der Recherche zu diesem Artikel habe ich zahlreiche Antworten auf Schüleranfragen gefunden, die so komplex waren, dass sie den Schüler unmöglich hätten aufklären können. In diesem Artikel werde ich alles tun, was ich kann, um diese Methode so einfach und zugänglich wie möglich zu machen.

Die Methode lässt sich am einfachsten als Algorithmus darstellen:

• Die Eckpunkte eines unregelmäßigen Polygons können als kartesische Koordinaten dargestellt werden: $x,y$.
• Jedes Koordinatenpaar wird in einem Flächensummenalgorithmus verarbeitet, der wie folgt aussieht:
  

  $A = A + \frac{(x_1 \Zeiten y_0 – y_1 \Zeiten x_0)}{2}$
  $A = A + \frac{(x_2 \Zeiten y_1 – y_2 \Zeiten x_1)}{2}$
  …

• Ein einfacher mathematischer Ausdruck für das Obige wäre:
  

  (2) Unregelmäßige Polygonfläche $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \mal y_i – y_{i+1} \mal x_i}$

• HINWEIS: In Gleichung (2) endet die durchlaufene Zahl mit dem letzten angegebenen Datenelement, sie wiederholt nicht das Anfangselement, wie in Gleichung (1) oben gezeigt. Für meine Zwecke, die weiter unten erläutert werden, ist diese Form beabsichtigt – in einer Landvermessung sollten die Felddaten die Abbildung abschließen, d. h. das letzte Element sollte dem ersten entsprechen. In einer solchen Anwendung würde ein automatisches Schließen der Abbildung wie in Gleichung (1) Fehler verbergen, die ausgewertet werden müssen.

  Benutzer können die in Gleichung (1) gezeigte Form für andere Zwecke als die Reduzierung von Vermessungsdaten bevorzugen. Für diese Zwecke wird bei der Verarbeitung einfach das erste Datenelement am Ende des Traversals neu ausgewertet, oder es werden Datensätze bereitgestellt, die das erste Datenelement als letztes wiederholen.

• Hier ist eine vollständige, funktionierende Python-Funktion:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Das „array“-Argument oben ist eine Menge kartesischer $x,y$-Koordinaten, d.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Beachten Sie bei diesem Datensatz, dass der erste Datensatz am Ende wiederholt wird.

• Hier ist eine etwas komplexere Python-Funktion, die sowohl die Fläche als auch die Umfangslänge berechnet:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Noch einmal diese Erinnerung: Bei den beiden obigen Codebeispielen sollte in anderen Anwendungen als der Reduzierung von Vermessungsdaten der bereitgestellte Datensatz eine Kopie des ersten Datenelements als letztes enthalten, d. h.

• Ich habe Python für diese Beispiele gewählt, weil ein Python-Listing die algorithmische Bedeutung maximiert und gleichzeitig den Ballast minimiert.

• Die obigen Funktionen können leicht in andere Sprachen konvertiert werden, fast direkt – mit Ausnahme der oben gezeigten Perimetersummierung, die die Tatsache ausnutzt, dass Python komplexe Zahlen unterstützt. Für Sprachen, die keine komplexen Zahlen unterstützen, kann man das Perimeterergebnis auf diese Weise erzeugen:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formell ist die Umfangslänge die Summe der Vektorbeträge:
  

  (3) Umfangslänge $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

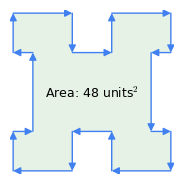
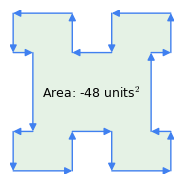Abbildung 1: Uhrzeigersinn vs. Vektoren gegen den Uhrzeigersinn

Hier einige wichtige Eigenschaften dieser Methode:

• Der gewählte Ursprungspunkt innerhalb des Polygons ist weder für die Flächen- noch für die Umfangsberechnung von Bedeutung, sondern nur, dass die Figur geschlossen ist, d.h. dass die letzte Koordinate gleich der letzten Koordinate ist.
• „Uhrzeigersinn-Regel“: Die Reihenfolge der Vektoren ist von Bedeutung – wenn der Umfang im Uhrzeigersinn durchlaufen wird, ist das Flächenergebnis positiv, wenn gegen den Uhrzeigersinn, ist es negativ (Abbildung 1). Es ist diese Eigenschaft der Methode, die die Fläche der Krümmungen von einer komplexen Figur wie in Abbildung 1 subtrahiert – die „Krümmungen“ stellen eine Traversierung gegen den Uhrzeigersinn innerhalb des Polygons dar.
• Viele Anwendungen dieser Methode verwenden ursprüngliche Datenquellen, die aus Polarvektoren bestehen (ein Beispiel sind rechtliche Beschreibungen der Landvermessung), aber diese Methode erfordert kartesische Koordinaten. Die Umwandlung von Polarkoordinaten in kartesische Koordinaten ist trivial, aber es ist wichtig, diese Anforderung im Auge zu behalten.
• Auch für eine genaue Flächenberechnung sollte das beschriebene Polygon eine geschlossene Figur sein – die letzte Koordinate sollte der ersten entsprechen. Bei Anwendungen, die Felddaten verwenden, die aus Längenvektoren bestehen, die anschließend in kartesische Form umgewandelt werden, ist es eine gute Idee, die kartesischen Anfangs- und Endkoordinaten zu vergleichen – sie sollten gleich sein. Ältere Landvermessungen (vor der Ära billiger Computerleistung) versagen beispielsweise regelmäßig bei diesem Test.

Dieser Abschnitt ist ein voll funktionsfähiger Flächen-/Perimeterrechner, der eingegebene kartesische oder polare Koordinatenpaare oder vermessungstechnische Beschreibungen verarbeiten kann. Wählen Sie einfach einen Datentyp (kartesische x,y-Koordinaten, polare m,θ-Koordinaten oder eine vermessungstechnische Beschreibung) und geben Sie die Daten in den Dateneingabebereich unten ein (oder fügen Sie sie ein). Sie können auch Beispieldatensätze auswählen, um sich mit dem Programm vertraut zu machen und zu üben.

Aus Gründen der Browsersicherheit müssen die Leser ihre Systemzwischenablage verwenden, um übermäßige Eingaben zu vermeiden und um große Datenmengen aus einer anderen Quelle zu importieren. Kopieren Sie einfach Daten in die Zwischenablage der Quellanwendung, klicken Sie dann auf den Dateneingabebereich darunter und drücken Sie Strg+A, um alles auszuwählen, Strg+V, um Daten von einer anderen Quelle zu übernehmen, und Strg+C, um Ihre eigenen eingegebenen Daten zu kopieren. Die meisten Browser bieten auch Funktionen für die Zwischenablage als Menüpunkte an.

Wählen Sie den Datentyp:

Kartesisch (x,y)

Polar (m,θ)

Vermessungsbeschreibung

Dateneingabebereich: Alles auswählen: Strg+A | Kopieren: Ctrl+C | Einfügen: Strg+V

Diagrammbereich:

Leider unterstützt Ihr Browser die für diese Funktion erforderlichen grafischen Fähigkeiten nicht –
erwägen Sie die Installation von Google Chrome oder Firefox.

Optionen:

Linien

Pfeile

Ursprung

Zentrum

Längeneinheit:

Linienbreite:

Umgekehrt

Ergebnisse:Alles auswählen: Strg+A | Kopieren: Ctrl+C | Einfügen: Strg+V

Der Flächen-/Perimeterrechner hat drei Eingabemodi:

• Kartesische (x,y) Koordinatenpaare:

  • Jede Koordinate ist eine zweidimensionale Position mit einem horizontalen (x) und einem vertikalen (y) Teil (eine kartesische Koordinate).
  • Die Koordinaten sind nicht kumulativ – jede beschreibt unabhängig ihre Position.
  • Ein Quadrat wäre also:
    • 0,0 (Ursprung)
    • 0,100 (oben)
    • 100,100 (rechts)
    • 100,0 (unten)
    • 0,0 (zurück zum Ursprung)
  

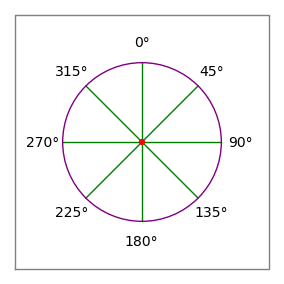  Abbildung 2: Windrose

  • Die Kommas im obigen Beispiel dienen nur dazu, die Datenpaare für den Leser zu gruppieren – sie haben keine Bedeutung für den Datenparser des Gebietscomputers.
  • Der Parser ist robust genug, dass das obige Beispiel in den Dateneingabebereich des Computers eingefügt werden kann und funktioniert (probieren Sie es aus).
  • Die einzige Einschränkung ist, dass erklärende Kommentare keine Zahlen enthalten dürfen.

• Polare (m,θ) Koordinatenpaare:

  • Jede Koordinate besteht aus einem Abstand und einem Winkel in Grad (einem polaren Vektor).
  • Die Winkel folgen der Kompasskonvention – 0 Grad ist nach oben oder „Norden“, 90 Grad ist nach rechts oder „Osten“ (Abbildung 2).
  • Im Gegensatz zur früheren kartesischen Form sind diese Koordinaten kumulativ – jeder neue Vektor addiert sich zu der aktuellen Position.
  • Ein Quadrat wäre also:
    • 100,0 (nach oben)
    • 100,90 (nach rechts)
    • 100,180 (nach unten)
    • 100,270 (zurück zum Ursprung)
  • Wie zuvor funktioniert dieses Beispiel, wenn es in den Dateneingabebereich des Computers eingefügt und der Polarmodus ausgewählt wird.
  • Bei Polarkoordinaten ist zu beachten, dass der Ursprung implizit und auf x = 0, y = 0 voreingestellt ist.
  

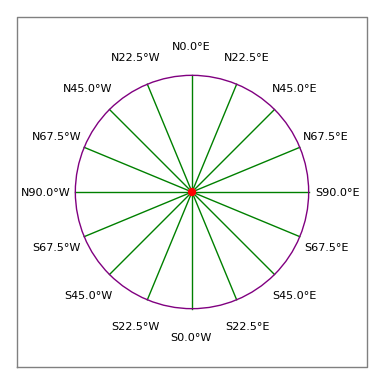  Abbildung 3: Kompassrose des Vermessungsingenieurs

• Rechtliche Beschreibung:

  • Zunächst eine Erläuterung des Zusammenhangs zwischen der Auswahl „Längeneinheiten“ und der Ergebnisanzeige:
    • Für jedes Polygon wird eine Liste von Flächenergebnissen unter Verwendung eines festen Satzes von gemeinsamen Flächeneinheiten (Fuß2, Meter2 usw.) berechnet. Damit diese Flächenliste aussagekräftig ist, müssen die eingegebenen Längeneinheiten bekannt sein.
    • Im kartesischen und polaren Modus haben die Dateneinträge keine Einheiten, so dass der Benutzer wählt, welche Einheiten er den Längen zuordnet. Wenn der Benutzer also die Längeneinheiten ändert, ändern sich die Flächenwerte und die Längenbezeichnungen, nicht aber die Längenwerte.
    • Im Vermessungsmodus enthält die rechtliche Beschreibung Längeneinheiten (Fuß, Meter usw.), was bedeutet, dass die Längeneinheiten von der Quelle vordefiniert sind. Wenn der Benutzer also die Längeneinheiten ändert, ändert dies die Längenbezeichnungen und -werte, nicht die Flächenwerte.
  • Der Vermessungsbeschreibungs-Parser ist bei weitem die unzuverlässigste der drei Daten-Parsing-Methoden – es handelt sich eher um ein Experiment als um eine robuste Datenkonvertierungsmethode.
  • Ich habe diesen Parser geschrieben, indem ich eine Reihe von Gesetzesbeschreibungen heruntergeladen habe (die als Beispiele im obigen Rechner enthalten sind) und den Code des Parsers so lange angepasst habe, bis alle erfolgreich dekodiert werden konnten.

  Die Kriterien für „Erfolg“ waren, dass das Ergebnis die gleiche quadratische Fläche wie die Beschreibung hat und dass die Abbildung „geschlossen“ ist.

  • Der Begriff „Abschluss“, und insbesondere der Abschlussfehler, wird in der Vermessungsarbeit verwendet, um den Grad zu beschreiben, in dem der Endpunkt des Vermessungsgangs mit dem Anfangspunkt übereinstimmt. Dies ist in der Realität nur selten der Fall – Fehler in der Schließung ergeben sich in der Regel aus Fehlern bei der Feldarbeit, und ältere Vermessungen, die vor dem Aufkommen billiger Computer veröffentlicht wurden, neigen dazu, eher schlechte Schließungen sowie sehr ungenaue Schätzungen der quadratischen Fläche aufzuweisen.
  • Eine vermessungstechnische Beschreibung ist eine formale Art und Weise, ein Grundstück zu beschreiben – ihre Form und Syntax hat sich über Jahrzehnte durch gegenseitig akzeptierte, etwas willkürliche Konventionen entwickelt, die von Vermessungsfachleuten geteilt werden.
  • Für diesen Flächen-/Perimeterrechner müssen die eingegebenen Daten bestimmten strengen Konventionen folgen, die einige, aber nicht alle vermessungstechnischen Beschreibungen einhalten. Die wesentlichen Elemente sind:
    • Das Vorhandensein des Begriffs „Anfangspunkt“, der einen vorläufigen Inhalt von demjenigen trennt, der die Abmessungen des beschriebenen Flurstücks beschreibt. In einigen Dokumenten heißt es „Wahrer Anfangspunkt“, in anderen „Tatsächlicher Anfangspunkt“ und in wieder anderen „Punkt des Beginns“. Ein erfolgreicher Parser muss den Inhalt vor dieser Phrase entfernen und alles danach beibehalten.
    • Eine Reihe von Phrasen, die eine spezielle Art von polarem Vektor beschreiben, der von Vermessern verwendet wird:
      • Das Wort „Nord“ oder „Süd“ oder seine Abkürzung „N“ oder „S“.
      • Dann ein Winkel, ausgedrückt in Grad, Minuten und Sekunden.
      • Dann das Wort „Ost“ oder „West“ oder seine Abkürzung „E“ oder „W“.
      • Dann eine Entfernung.
      • Dann eine Entfernungseinheit – Fuß, Meter usw.
  • Hier sind einige verschiedene Beispiele für Vermessungsvektoren aus den Musterrechtsbeschreibungen:
    • N 2°0’0″ W – 63.50 feet
    • N90°00’00 „W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.86 feet
    • S. 22 degrees 41′ 55″ E. 174.10 feet
  • Bei den obigen Beispielen ist zu beachten, dass sie alle eine unterschiedliche Syntax haben. Es gibt viele rechtliche Beschreibungen, die dieser Parser nicht erfolgreich entschlüsseln kann, nur weil ich nicht versucht habe, ihre Syntax zu übernehmen. Aber es ist wichtig, hinzuzufügen, dass ein wirklich robuster Parser für die Vielzahl der existierenden rechtlichen Beschreibungen so schlau wie Watson sein müsste.
  • Die Benutzer dieses Gebiets-/Perimeter-Computers sollten es vermeiden, rechtliche Beschreibungen im Klartext einzureichen und zu hoffen, dass der Parser es herausfindet. Um direkte Eingaben von Hand zu machen (oder um eine Liste von Traversen zu erstellen, die an anderer Stelle importiert werden können), verwenden Sie diese Konvention:
    • Denken Sie daran, dass ein akzeptabler Traverseneintrag aus dem Wort „Nord“ oder „Süd“ oder dem Buchstaben „N“ oder „S“ besteht, gefolgt von bis zu drei Zahlen, die Grad, Minuten und Sekunden des Winkels angeben, gefolgt von dem Wort „Ost“ oder „West“ oder dem Buchstaben „E“ oder „W“, gefolgt von einer Entfernung, gefolgt von einer Entfernungseinheit.
    • Ein akzeptabler Eintrag wäre also „N 30 15 45 W 100 Fuß“, was bedeutet, dass eine Strecke von 100 Fuß 30 Grad, 15 Minuten und 45 Sekunden westlich von Norden liegt (d. h. ungefähr 330 Kompassgrade, siehe Abbildung 3).
    • Die Einträge für Minuten und Sekunden können übersprungen werden, wenn sie gleich Null sind, oder wenn der Eintrag in Dezimalgraden oder Grad und Dezimalminuten erfolgt.
  • Es ist nicht schwierig, eine gedruckte rechtliche Beschreibung in solche Einträge umzuwandeln, und es gibt eine Reihe von Möglichkeiten, Fehler zu erkennen. Wenn nach der Eingabe aller Traversen die Abbildung keinen Abschlussfehler aufweist und die gleiche quadratische Fläche wie das Original angibt, sind die Einträge wahrscheinlich korrekt (oder sie weisen die gleichen Fehler wie die Originalbeschreibung auf).
  • Wenn nach der Eingabe einer rechtlichen Beschreibung auf diese Weise ein inakzeptabler Abschlussfehler auftritt oder die quadratische Fläche falsch ist, denken Sie daran, dass die Originaldaten falsch sein könnten. Es gibt jede Menge rechtlicher Beschreibungen, die nie mit einer Computermethode wie dieser überprüft wurden und die nie korrekt waren.

Beim Durchsehen der kartesischen (x,y) Beispiele fällt das Verhältnis von Fläche zu Umfang der verschiedenen Formen auf. Das „seltsam geformte Polygon“ hat ein mittleres Verhältnis, der Kreis hat das kleinste Verhältnis, und der Hilbert-Raum hat bei weitem das größte Verhältnis. Dieses Verhältnis erstreckt sich auch auf höhere Dimensionen, wo eine Kugel bekanntlich das größte Volumen pro Fläche hat.

Zum Kreisbeispiel: Es handelt sich um einen „Einheitskreis“, einen Kreis mit dem Radius eins. Für das angegebene Beispiel entspricht die Fläche ungefähr $\pi$ und der Umfang ungefähr $2\pi$, die richtigen Werte für einen Einheitskreis. Damit diese Werte mehr als Näherungen sind, nämlich genau $\pi$ und $2\pi$, müsste die Anzahl der Polygonseiten unendlich sein. Ich habe mich dagegen entschieden 🙂

Das Beispiel für den Hilbert-Raum wurde mit einem Sage-Algorithmus mit einer bescheidenen Ordnungswahl erzeugt (um nicht zu viele Daten zu erzeugen). Im Prinzip kann ein Hilbert-Raum ein unendliches Verhältnis von Umfang zu Fläche in zwei Dimensionen oder von Oberfläche zu Volumen in drei Dimensionen haben. Um zu sehen, wie komplex ein Hilbert-Raum werden kann, klicken Sie hier, um einen Hilbert-Raum der Ordnung 7 zu sehen.

Beim Hilbert-Beispiel ist zu beachten, dass die berechnete Fläche für eine 1×1-Fläche nahe bei 1/2 liegt. Im Idealfall, ohne die Notwendigkeit, eine Linienfigur in eine Flächenfigur umzuwandeln, und mit dem richtigen Algorithmus, wäre die Fläche genau 1/2 der Fläche eines Quadrats mit den gleichen Abmessungen.

Der polare Eingabemodus ist mehr oder weniger gleichwertig mit der Schildkrötengrafik, wenn man Null Grad für „oben“, 90 Grad für „rechts“ usw. ersetzt und wenn jede Dreh- und Bewegungssequenz in einem Befehl zusammengefasst wird. Die Verwendung des polaren Eingabemodus ist ein einfacher Weg, um eine komplexe Form von Hand zu konstruieren, da Entfernungen und Winkel leichter zu verfolgen sind als kartesische Koordinaten.

Ich habe die oben beschriebene Methode zur Berechnung von Landvermessungsflächen zum ersten Mal vor Jahren verwendet, als ich im ländlichen Oregon lebte, umgeben von Leuten, die die Fläche und den Umfang ihrer Grundstücke wissen mussten. Ich bin auf viele schockierende Beispiele gestoßen, in denen Immobilienmakler die Leute schamlos betrogen haben, die keine Möglichkeit hatten, herauszufinden, was los war. Bei vielen Gelegenheiten berechnete ich eine Fläche anhand einer rechtlichen Beschreibung, nur um dann festzustellen, dass die in der Garantieurkunde angegebene Fläche völlig ungenau war – und immer höher als die Realität.

Bei einer Gelegenheit wurde ich gebeten, ein Grundstück in zwei gleiche Abschnitte zu teilen und für jeden eine rechtliche Beschreibung zu erstellen. Da ich einen neu erworbenen Apple II besaß (der die Rechenleistung eines modernen Bleistiftspitzers hatte), war dies sehr einfach – aber während der Arbeit stellte ich fest, dass die Gesamtfläche um etwa drei Hektar, d.h. etwa 25 % der Gesamtfläche, falsch war. Ich wandte mich an die Grundstücksgesellschaft, die mir dreist antwortete: „Sehen Sie hier, wo in der Urkunde ‚mehr oder weniger‘ steht?“

Bei einer anderen Gelegenheit begann ich mit dem Kauf eines Grundstücks, aber durch die obige Erfahrung vorgewarnt, beschloss ich, als ich die Eigentumsurkunde erhielt, die rechtliche Beschreibung in mein Programm einzugeben, um zu sehen, ob die Flächenangabe korrekt war. Zu meinem Entsetzen musste ich jedoch feststellen, dass alle Titelpolicen für die Parzellen in diesem Abschnitt dieselbe rechtliche Beschreibung enthielten – die des ersten vermessenen Grundstücks. Es stellte sich heraus, dass die Erschließungsfirma beschlossen hatte, Geld zu sparen, indem sie nur eines der Dutzenden von zum Verkauf angebotenen Grundstücken vermessen ließ und diese rechtliche Beschreibung in alle Titelpolicen aufnahm. Sie waren sich sicher, dass sie damit durchkommen würden – denn wer versteht schon etwas von Mathematik?

Nach einem Streit mit der Grundstücksgesellschaft und dem Erschließungsunternehmen und dem Versuch, sie davon zu überzeugen, für Vermessungen zu bezahlen, damit die rechtlichen Beschreibungen keine höflichen Fiktionen waren, gab ich auf und beschloss, das Grundstück nicht zu kaufen. Es war, als würde man herausfinden, wie Wurst gemacht wird – man kann zu viel wissen.

• 04.15.2013 Version 1.3. Detaillierte Erklärung des Standard-Datenformats hinzugefügt, d.h. Listen, die den ersten Datenpunkt als letzten wiederholen.
• 03.24.2013 Version 1.2. Weitere Optimierung des Vermessungsbeschreibungsparsers, Hinzufügen weiterer Ergebnisdatenfelder.
• 03.23.2013 Version 1.1. Verbesserte den Parser für rechtliche Beschreibungen, um mit mehr Arten von Beschreibungen umzugehen, fügte einen Selektor für Längeneinheiten und eine Ergebnisliste von Flächen in gemeinsamen Einheiten hinzu.
• 03.22.2013 Version 1.0. Erste öffentliche Version.