Die logistische Gleichung (manchmal auch Verhulst-Modell oder logistische Wachstumskurve genannt) ist ein Modell des Bevölkerungswachstums, das erstmals von Pierre Verhulst (1845, 1847) veröffentlicht wurde. Das Modell ist zeitlich kontinuierlich, aber eine Modifikation der kontinuierlichen Gleichung zu einer diskreten quadratischen Rekursionsgleichung, die als logistische Karte bekannt ist, wird ebenfalls häufig verwendet.
Die kontinuierliche Version des logistischen Modells wird durch die Differentialgleichung
 |
(1)
|
beschrieben, wobei 
der Malthus’sche Parameter (Rate des maximalen Bevölkerungswachstums) und 
die sogenannte Tragfähigkeit (d.h., die maximal tragbare Bevölkerung). Dividiert man beide Seiten durch 
und definiert 
, erhält man die Differentialgleichung
 |
(2)
|
, die als als logistische Gleichung bezeichnet wird und die Lösung
 |
(3)
|
Die Funktion 
wird manchmal als Sigmoidfunktion bezeichnet.
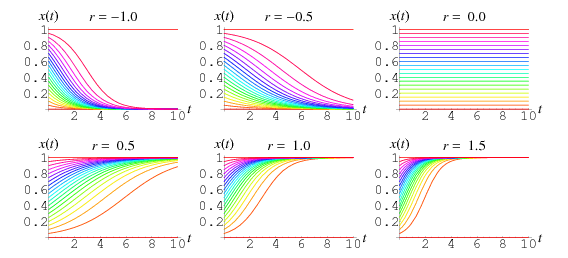
Während 
normalerweise positiv sein muss, werden Diagramme der obigen Lösung für verschiedene positive und negative Werte von 
und Anfangsbedingungen 
gezeigt, die von 0,00 bis 1,00 in Schritten von 0,05 reichen.
Die diskrete Version der logistischen Gleichung (3) ist als logistische Karte bekannt.
Die Kurve
 |
(4)
|
, die sich aus (3) ergibt, wird manchmal als logistische Kurve bezeichnet. In ähnlicher Weise wird eine normalisierte Form der Gleichung (3) üblicherweise als statistische Verteilung verwendet, die als logistische Verteilung bekannt ist.