Im heutigen Beitrag wirst du den Unterschied zwischen Primzahlen und zusammengesetzten Zahlen kennenlernen. Außerdem zeigen wir dir einige Beispiele, damit du sie besser verstehen kannst.
Index
Was sind Primzahlen?
Primzahlen sind die Zahlen, die nur durch sich selbst und 1 teilbar sind, das heißt, wenn man versucht, sie durch eine andere Zahl zu teilen, ist das Ergebnis keine ganze Zahl. Wenn man die Zahl also durch etwas anderes als durch 1 oder sich selbst teilt, erhält man einen Rest, der nicht Null ist.
Primzahlen bis 100
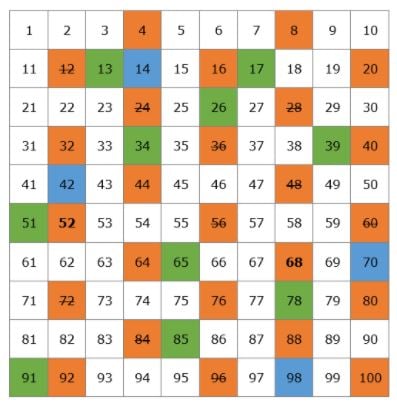
Wir werden eine Tabelle mit allen Primzahlen erstellen, die es bis 100 gibt.
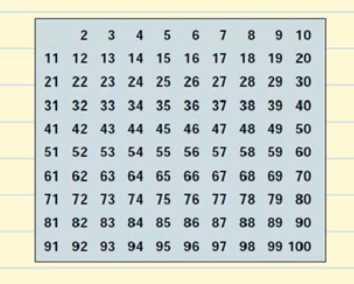
Fangen wir mit 2 an. 2 ist eine Primzahl, aber alle Vielfachen von 2 sind zusammengesetzte Zahlen, da sie durch 2 teilbar sind. Wir streichen alle Vielfachen von 2 in der Tabelle durch.
Die nächste Primzahl ist 3, also können wir alle Vielfachen von 3 durchstreichen, da sie zusammengesetzte Zahlen sein werden.
Nach 3 kommt die nächste Primzahl 5, also streichen wir alle Vielfachen von 5 durch.
Dann haben wir die Primzahl 7 und wir streichen alle Vielfachen von 7 durch.
Die nächste Primzahl ist 11, also streichen wir alle Vielfachen von 11, nämlich 22, 33, 44, 55, 66, 77, 88 und 99. Alle diese Zahlen wurden bereits durchgestrichen, so dass wir nun alle zusammengesetzten Zahlen auf unserer Tabelle durchgestrichen haben.

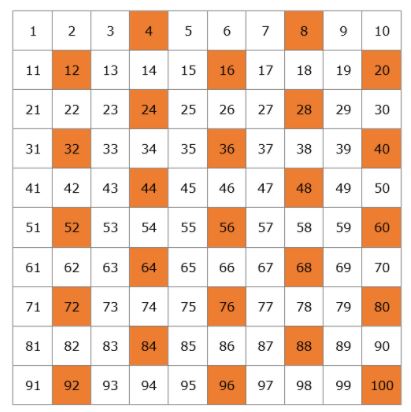
Das ist unsere Liste der Primzahlen von 1 bis 100. Du musst sie nicht auswendig lernen, aber es wäre am besten, wenn du dir die kleineren Zahlen merken würdest, wie 2, 3, 5, 7, 11, 13.
Wie viele Primzahlen gibt es?
Der griechische Mathematiker Eratosthenes (3. Jahrhundert v. Chr.) entwickelte eine schnelle Methode, um alle Primzahlen bis zu einer bestimmten Zahl zu finden. Dieses Verfahren wird das Sieb des Eratosthenes genannt.
Beachte, dass es zwischen 1 und 100 25 Primzahlen gibt. Wie viele Primzahlen gibt es insgesamt? Seit der Antike weiß man, dass es unendlich viele gibt, daher ist es unmöglich, sie alle aufzuzählen. Da Euklid, der im 4. Jahrhundert v. Chr. als erster zeigte, dass es eine unendliche Menge gibt, das Konzept der Unendlichkeit nicht kannte, sagte er: „Primzahlen sind mehr als jede feste Anzahl von ihnen“, was bedeutet, dass es mehr gibt, wenn man sich 100 vorstellt, und noch mehr, wenn man sich eine Million vorstellt.
Primzahlen 100 bis 1.000
Werfen wir einen Blick auf die Primzahlen von 100 bis 1.000.

Es tut uns leid, dass wir nicht alle zeigen können, denn ihr wisst ja, dass es unendlich viele gibt. 😉
Primzahlen Beispiele
Um die Primzahlen besser zu verstehen, werden wir eine Übung erklären.
Sara hat 6 Bonbons, die sie teilen möchte, aber sie weiß nicht, mit wie vielen Leuten sie sie teilen kann, damit alle die gleiche Menge bekommen und nichts übrig bleibt. Auf wie viele Arten kann sie das tun?
Hier ist Sara und ihre 6 Bonbons:

Wie können wir sie aufteilen?
Die erste und einfachste Möglichkeit ist, sie einer Person zu geben, also durch 1 zu teilen. Auf diese Weise hat diese Person 6 Bonbons.
Die nächste Möglichkeit ist, sie zwischen 2 Personen aufzuteilen. Da 6 geteilt durch 2 gleich 3 ist, bekommt jede Person 3 Bonbons!

Wir machen weiter mit der nächsten Zahl, 3. Wenn wir 6 Bonbons auf 3 Personen aufteilen, ist das auch eine exakte Teilung und jede Person bekommt 2 Bonbons:

Lassen Sie uns mit den Zahlen fortfahren. Bei 4 und 5 gibt es keine exakten Divisionen, aber bei 6 schon.
Da 6 geteilt durch 6 1 ist, können wir 6 Kindern je 1 Bonbon geben.

Wir werden einige Informationen sammeln. Wir haben 6 Bonbons, die wir (mit einer genauen Aufteilung) zwischen 1, 2, 3 und 6 Personen aufteilen können. Mit anderen Worten: Wir können die Zahl 6 teilen und erhalten 0 als Rest, wenn wir sie durch 1, 2, 3 und 6 teilen. Diese Zahlen nennt man die Teiler von 6.
Wir versuchen es mit einer anderen Zahl, zum Beispiel 7.
Nun hat Sara 7 Bonbons und möchte sie teilen, weiß aber nicht, mit wie vielen Leuten sie sie teilen kann, damit alle die gleiche Menge bekommen und nichts übrig bleibt. Auf wie viele Arten kann sie das tun?

Henry ist so glücklich! Er hat alle Bonbons bekommen!
Kann man das auch anders machen? Wir können 7 nicht durch 2, 3, 4, 5 oder 6 teilen, …aber 7 ist möglich!
Sara kann die Bonbons unter 7 Personen aufteilen, indem sie ihnen jeweils ein Bonbon gibt:

So kann 7 nur durch 1 und 7 geteilt werden, seine einzigen Teiler sind 1 und 7. Diese Art von Zahlen nennen wir Primzahlen.
Gibt es noch mehr Primzahlen? Ja, natürlich! Lass uns nach weiteren suchen:
- Ist 4? Nein! Denn ihre Teiler sind 1, 2 und 4.
- Ist 5? Ja! Weil seine Teiler 1 und 5 sind.
- Ist 8? Nein! Weil ihre Teiler 1, 2, 4 und 8 sind.
Kurz gesagt, eine Zahl ist prim, wenn sie nur 2 Teiler hat: 1 und sich selbst.
Jetzt kannst du nach vielen Primzahlen suchen!
Wie man Primzahlen findet
Pass gut auf! Wir geben dir einen Trick an die Hand, mit dem du herausfinden kannst, ob eine Zahl eine Primzahl ist oder nicht, ohne nach ihren Teilern suchen zu müssen, sondern auf eine Art und Weise, die mehr Spaß macht und uns die Teiler liefert (wenn sie welche haben).
Wählen wir eine beliebige Zahl, zum Beispiel 16.
Um zu überprüfen, ob es sich um eine Primzahl handelt oder nicht, verwenden wir eine Tabelle, die den Montessori-Karten zum Multiplizieren sehr ähnlich ist. Und wir bekommen so viele Kugeln wie die Zahl, die wir gewählt haben. In diesem Fall sind es 16 Kugeln.
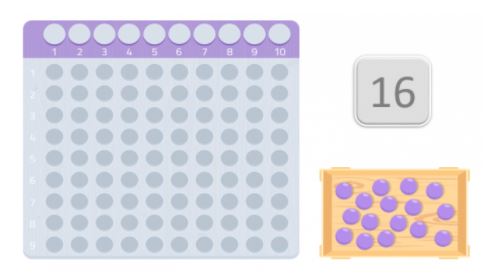
Wenn wir die Tabelle und die Kugeln haben, sollten wir sie auf dem Tisch platzieren, beginnend mit dem ersten Feld, und versuchen, ein Rechteck zu bilden. Die Zahlen, die die Ränder des Rechtecks bilden, sind die Teiler dieser Zahl.
Wenn es uns gelingt, nur mit der gleichen Zahl, die wir verwenden, und der Zahl 1 ein Rechteck zu bilden, wird es eine Primzahl sein.
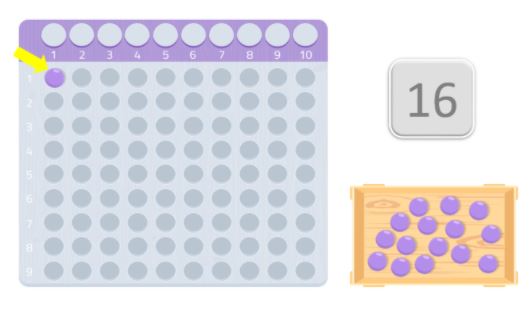
In diesem Fall legen wir zum Beispiel 8 Kugeln in die erste Reihe und 8 weitere in die zweite. Wie du siehst, haben wir ein Rechteck gebildet, und wir sehen, dass 8, wie auch 2, Teiler der Zahl 16 sind. Daher ist 16 keine Primzahl, denn wie du weißt, sind Primzahlen diejenigen, die nur durch sich selbst und 1 teilbar sind.
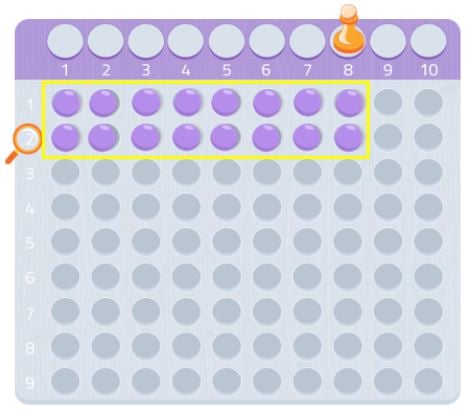
Wir können es mit einer anderen Zahl versuchen, zum Beispiel 7.
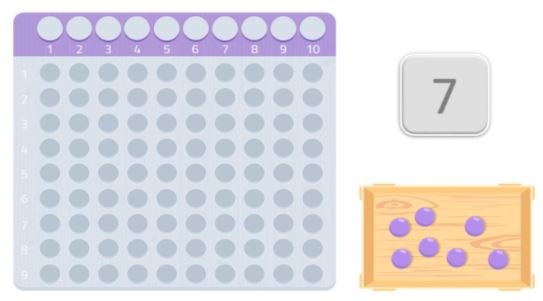
Wie wir sehen, können wir kein vollständiges Rechteck bilden, es würde uns eine Kugel fehlen. Da wir nicht in der Lage sind, ein Rechteck zu bilden, können wir sagen, dass die Zahl 7 keine anderen Teiler außer sich selbst und 1 hat, wie wir in der folgenden Abbildung sehen können.
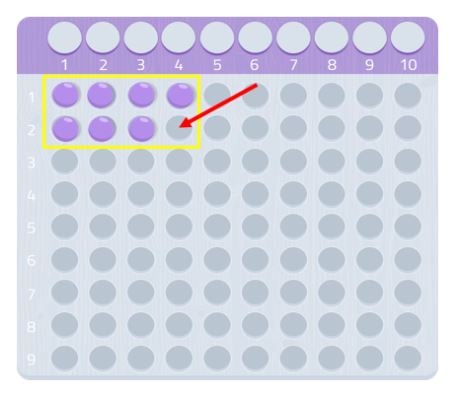
Daher ist 7 eine Primzahl!
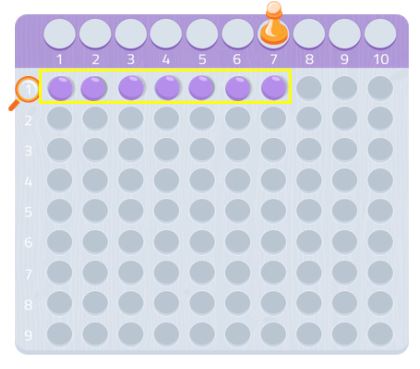
Versuch es mit jeder anderen Zahl, du wirst sehen, wie es funktioniert! Du kannst Diagrammpapier verwenden und nach Rechtecken mit dieser Anzahl von Quadraten suchen.
Warum sind Primzahlen wichtig?
Primzahlen sind der Schlüssel zur Arithmetik. Im Folgenden siehst du ein Beispiel, das ihre Bedeutung nicht nur in der Mathematik, sondern auch in der Natur zeigt.
Was bedeutet es, wenn wir sagen, dass Primzahlen der Schlüssel zur Arithmetik sind?
Das liegt daran, dass jede Zahl aus einem einzigartigen Produkt aus einer Reihe dieser Zahlen besteht.
Man nimmt an, dass sie seit etwa 20.000 Jahren erforscht werden, als ein Vorfahr von uns eine Reihe von Primzahlen (11, 13, 17 und 19) auf dem Ishango-Knochen aufschrieb. Als ob dies ein Zufall wäre, wurde bestätigt, dass die alten Ägypter bereits vor 4.000 Jahren mit ihnen arbeiteten.
Darüber hinaus kennt die Natur sie sehr gut, und einige Arten konnten sie im Laufe ihrer Evolution entdecken und für ihr Überleben nutzen.
Ich beziehe mich auf mehrere Zikadenarten, wie die Magicicada septendecium, die in Nordamerika lebt. Diese Zikadenart hat ihren Brutzyklus auf 13 oder 17 Jahre festgelegt, nicht 12, 14, 15, 16 oder 18 – genau 13 oder 17. Dadurch kann sie Raubtieren ausweichen, die ebenfalls periodische Fortpflanzungszyklen haben; man stelle sich ein Raubtier mit einem vierjährigen Fortpflanzungszyklus vor.
Wenn der Lebenszyklus einer Zikade 12 oder 14 Jahre betragen würde, würde er sehr häufig mit einem Raubtier zusammenfallen, viel häufiger als wenn er 13 oder 17 Jahre betragen würde. Genau 2 Mal alle 100 Jahre, während sie sonst in 11 Zyklen zusammentreffen würden, was die Entwicklung der Art gefährden würde.
Auch die Sicherheit der elektronischen Kommunikation basiert auf Primzahlen. Jede verschlüsselte Nachricht, die über das Internet verschickt wird (Nachrichtennetzwerke, Einkäufe oder elektronisches Bankwesen), ist mit einer großen Zahl verbunden, und es ist sehr schwierig zu wissen, ob sie eine Primzahl ist oder nicht. Der Empfänger hat einen ihrer Teiler und kann sie deshalb entschlüsseln. Primzahlen sind also entscheidend für unsere Privatsphäre bei der elektronischen Kommunikation.
Was sind zusammengesetzte Zahlen?
Zusammengesetzte Zahlen sind Zahlen, die sowohl durch 1 und sich selbst als auch durch andere Zahlen teilbar sind.
Wir werden uns ein Beispiel für eine Primzahl und eine zusammengesetzte Zahl ansehen.
11 kann als Multiplikation 1 x 11 geschrieben werden, aber sie kann nicht als irgendeine andere Multiplikation natürlicher Zahlen geschrieben werden. Sie hat nur die Teiler 1 und 11 und ist daher eine Primzahl.
12 kann als Multiplikation 1 x 12 und als Multiplikation 3 x 4 und 2 x 6 geschrieben werden. Da 12 durch mehr Zahlen als 1 und sich selbst teilbar ist, ist 12 eine zusammengesetzte Zahl.
Ist 1 eine Primzahl?
Es gibt Leute, die das glauben, weil sie sagen, dass 1 nur durch 1 und sich selbst geteilt werden kann, aber in der Mathematik ist die Zahl 1 als Primzahl verworfen worden, weil sie nur einen Teiler hat. Tatsächlich wird das Kriterium „eine positive ganze Zahl ist primär, wenn sie genau zwei positive Teiler hat“ verwendet, um die Zahl 1 aus der Liste der Primzahlen auszuschließen. Das liegt nicht daran, dass wir pingelig sind, aber wenn die Zahl 1 als Primzahl gelten würde, müssten viele mathematische Eigenschaften anders ausgedrückt werden.
So, 1 ist eine zusammengesetzte Zahl?
Nun, sie ist auch nicht zusammengesetzt, da sie nicht als Produkt von Primzahlen gesetzt werden kann. Die Zahl 1 ist weder prim noch zusammengesetzt. Und bevor du fragst, die Null ist auch nicht prim oder zusammengesetzt, aber das liegt daran, dass alle Überlegungen, die wir für positive Zahlen erklärt haben, also größer als Null sind.
Teiler einer Zahl
Der Teiler einer Zahl ist der Wert, der die Zahl in exakte Teile teilt, mit anderen Worten, einen Rest von 0 hat.
Als Beispiel wollen wir die Teiler von 24 berechnen.
Wir beginnen mit der kleinsten Zahl, die mit 1 beginnt.
- 24 / 1 = 24. Sowohl 1 als auch 24 sind Teiler.
- 24 / 2 = 12. Also sind 2 und 12 Teiler.
- 24 / 3 = 8. Also sind 3 und 8 Teiler.
- 24 / 4 = 6. Also sind 4 und 6 Teiler.
- 24 / 5 = 4. Es ist keine exakte Division und hat einen Rest von 4, also ist 5 kein Teiler.
Die nächste Zahl ist 6, aber da wir bereits wissen, dass 6 ein Teiler von 24 ist, haben wir die Berechnung der Teiler für 24 abgeschlossen.
Video: Faktorisierung und Primzahlen
Wenn du mehr über Primzahlen und zusammengesetzte Zahlen wissen möchtest, schau dir das folgende Video an. Sie lernen auch das Konzept der Faktorisierung anhand der Montessori-Tabelle kennen.
Dieses Video ist eines unserer interaktiven Lernprogramme. Obwohl es nicht interaktiv ist, können Sie es sich so oft wie nötig ansehen und es mit Freunden teilen. Wenn Sie Zugang zu unseren interaktiven Tutorials haben möchten, registrieren Sie sich bei Smartick! Die Online-Methode, die Kindern im Alter von 4 bis 14 Jahren hilft, Mathematik zu lernen und zu üben.
Wenn du weiter über Primzahlen und die beste Mathematik für dein Niveau lernen möchtest, registriere dich bei Smartick und probiere es kostenlos aus!
Mehr erfahren:
- Primzahlen und zusammengesetzte Zahlen
- Primzahlen: Ein Trick, um sie zu erkennen
- Hauptzahlen: Wie man sie mit dem Sieb des Eratosthenes findet
- Lernen Sie, wie man mit Primzahlen faktorisiert
- Primzahlenaktivitäten mit Smartick



- Autor
- Recent Posts
Ein multidisziplinäres und multikulturelles Team, das sich aus Mathematikern, Lehrern, Professoren und anderen Bildungsexperten zusammensetzt!
Sie bemühen sich, die bestmöglichen mathematischen Inhalte zu erstellen.
- Beispiele für Mathe-Wortaufgaben der 3. Klasse mit Lösungen – 25.03.2021
- Aufeinanderfolgende Innenwinkel: Was sie sind und wie man sie findet mit Beispielen – 03/11/2021
- Beispiele für Wortprobleme der zweiten Klasse mit Lösungen – 02/04/2021