DS:n laskeminen termodynaamisista sykleistä
Voidaan myös laskea entropian muutos termodynaamisen syklin avulla. Kuten aiemmin opit, molaarinen lämpökapasiteetti (Cp) on lämpömäärä, joka tarvitaan nostamaan 1 mol aineen lämpötilaa 1 °C:lla vakiopaineessa. Vastaavasti Cv on lämpömäärä, joka tarvitaan nostamaan 1 mol aineen lämpötilaa 1 °C:lla vakiotilavuudessa. Entropian kasvu lämpötilan kasvaessa kuvassa \(\PageIndex{2}\) on suunnilleen verrannollinen aineen lämpökapasiteettiin.
Muistutetaan, että entropian muutos (ΔS) liittyy lämpövirtaan (qrev) kaavalla ΔS = qrev/T. Koska qrev = nCpΔT vakiopaineessa tai nCvΔT vakiotilavuudessa, missä n on läsnä olevien ainemoolien lukumäärä, entropian muutos aineessa, jonka lämpötila muuttuu T1:stä T2:een, on seuraava:
\
Kuten huomaat edistyneemmillä matematiikan kursseilla kuin mitä tässä vaaditaan, voidaan osoittaa, että tämä on yhtä suuri kuin: Luonnollisten logaritmien tarkastelu, ks. perustaidot 6 luvussa 11 ”Nesteet”.
\
Samoin,
\
Siten voimme käyttää yhdistelmää lämpökapasiteettimittauksista (Yhtälö 18.20 tai Yhtälö 18.21) ja kokeellisesti mitatuista fuusio- tai höyrystymisentalpioiden arvoista, jos kyseessä on faasimuutos (Yhtälö 18.18) laskeaksemme näytteen lämpötilan muutosta vastaavan entropian muutoksen.
Voidaan käyttää termodynaamista sykliä entropian muutoksen laskemiseen silloin, kun rikin kaltaisen aineen faasimuutosta ei voida mitata suoraan. Kuten esimerkin 6 harjoituksessa todettiin, alkuainerikkiä esiintyy kahdessa muodossa (kuvan \(\PageIndex{3}\) osa a)): orthorhombisessa muodossa, jolla on hyvin järjestäytynyt rakenne (Sα), ja vähemmän järjestäytyneessä monokliinisessä muodossa (Sβ). Orthorhombinen (α) muoto on vakaampi huoneenlämmössä, mutta tapahtuu faasimuutos monokliiniseen (β) muotoon yli 95,3 °C:n (368,5 K) lämpötiloissa. Siirtyminen Sα:sta Sβ:hen voidaan kuvata kuvan \(\PageIndex{3}\) osassa (b) esitetyllä termodynaamisella syklillä, jossa nestemäinen rikki on välivaihe. Entropian muutosta, joka liittyy nestemäisen rikin muuttumiseen Sβ:ksi (-ΔSfus(β) = ΔS3 syklissä), ei voida mitata suoraan. Koska entropia on tilafunktio, ΔS3 voidaan kuitenkin laskea Sα-Sβ-siirtymän kokonaisentropian muutoksesta (ΔSt), joka on yhtä suuri kuin termodynaamisen syklin vaiheiden ΔS-arvojen summa, yhtälön 18 avulla.20 ja taulukoituja termodynaamisia parametreja (Sα:n ja Sβ:n lämpökapasiteetit ΔHfus(α) ja Sα:n sulamispiste.)

Luotaamalla ΔS3:n arvoksi saadaan -3,24 J/(mol-K). Odotetusti vähemmän järjestäytyneen tilan (neste) muuttuessa järjestäytyneemmäksi (kide) ΔS3 on negatiivinen.
Miten entropiat mitataan
Aineen absoluuttinen entropia missä tahansa 0 K:n yläpuolella olevassa lämpötilassa on määritettävä laskemalla lämmöntuoton lisäykset q, jotka tarvitaan aineen saattamiseksi 0 K:sta kiinnostavaan lämpötilaan, ja summaamalla sitten suhdeluvut q/T. Tarvitaan kahdenlaisia kokeellisia mittauksia:
- Aineen mahdollisiin faasimuutoksiin liittyvät entalpiat kiinnostavalla lämpötila-alueella. Kiinteän aineen sulaminen ja nesteen höyrystyminen vastaavat lämpöenergian vastaanottamiseen käytettävissä olevien mikrotilojen lukumäärän huomattavaa lisääntymistä, joten näiden prosessien tapahtuessa systeemiin virtaa energiaa, joka täyttää nämä uudet mikrotilat siinä määrin kuin on tarpeen vakiolämpötilan (jäätymis- tai kiehumispisteen) ylläpitämiseksi; nämä lämpöenergian virtaukset vastaavat fuusio- ja höyrystymislämpöjä. Esimerkiksi sulamiseen liittyvä entropian lisäys on vain ΔHfuusio/Tm.
- Faasin lämpökapasiteetti C ilmaisee lämpömäärän, joka tarvitaan lämpötilan muuttamiseen pienellä määrällä ΔT , tai tarkemmin sanottuna äärettömän pienellä määrällä dT . Näin ollen entropian lisäys, joka aiheutuu aineen lämpenemisestä lämpötila-alueella, joka ei sisällä faasimuutosta, saadaan suureiden C dT/T summana kutakin lämpötilan lisäystä dT kohti. Tämä on tietenkin vain integraali
\
Koska lämpökapasiteetti on itsessään hieman lämpötilariippuvainen, absoluuttisten entropioiden tarkimmat määritykset edellyttävät, että edellä esitetyssä integraalissa käytetään C:n funktionaalista riippuvuutta T:stä vakion C sijasta.
\
Jos tätä ei tiedetä, voidaan ottaa sarja lämpökapasiteettimittauksia kapeilla lämpötilaväleillä ΔT ja mitata pinta-ala kunkin käyrän osan alla.
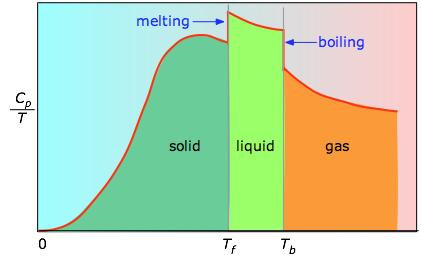
Käyrän kunkin jakson alapuolella oleva pinta-ala edustaa entropian muutosta, joka liittyy aineen lämmittämiseen välin ΔT läpi. Tähän on lisättävä sulamisen, höyrystymisen ja kiinteiden ja kiinteiden faasimuutosten entalpiat. Cp:n arvoja lämpötiloissa lähellä nollaa ei mitata suoraan, vaan ne voidaan arvioida kvanttiteorian avulla.
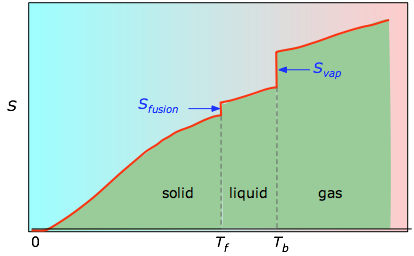
Kumulatiiviset pinta-alat 0 K:sta mihin tahansa lämpötilaan (jotka on otettu vasemmalla olevasta kokeellisesta kuvaajasta) piirretään sitten T:n funktiona, ja mahdolliset faasimuutosentropiat, kuten Svap = Hvap / Tb, lisätään, jotta saadaan absoluuttinen entropia lämpötilassa T.