Epäsäännöllisen monikulmion pinta-ala

Tässä artikkelissa kuvataan yksinkertainen ratkaisu geometriseen ongelmaan, joka on mielestäni kuvattu verkossa liian monimutkaisilla tavoilla. Ongelmana on laskea kaksiulotteisen, suljetun kuvion, kuten huoneen pohjapiirroksen tai tontin, tai minkä tahansa muun kaksiulotteisen rajatun kuvion (”epäsäännöllinen monikulmio”) pinta-ala ja ympärysmitan pituus, riippumatta siitä, kuinka monimutkainen se on.

En todellakaan väitä tämän menetelmän olevan omaperäinen. Versioita on ollut olemassa Gaussin ajoista lähtien tai sitä ennen. Mutta useimmat verkkoartikkelit kuvaavat menetelmää tarpeettoman monimutkaisella tavalla. Viitteitä ovat muun muassa Wikipedian Shoelace Formula -artikkeli, yhtä monimutkainen menetelmä Polygon-artikkelissa ja joukko artikkeleita, jotka vaikuttavat lasketuilta enemmänkin osoittamaan kirjoittajan oppineisuutta kuin tarjoamaan menetelmän vähiten monimutkaisen ilmentymän. Tässä artikkelissa (PDF) esitetään yksi vähiten monimutkaisista (mutta ei suinkaan yksinkertaisista) lausekkeista:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\\ \end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\\ y_1 & y_2\\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\\ y_2 & y_3\\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\\ y_{n-2} & y_{n-1}\\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\\ y_{n-1} & y_0\\\ \end{array} \right| \right\}$

Missä $x_n,y_n$ on monikulmion kärki ilmaistuna kartesiankoordinaatistossa, ja $\left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\\ \end{array} \right|$ viittaa determinanttiin, jonka arvo on $x_0 \times y_1 – y_0 \times x_1$

Älä lannistu yllä olevasta selostuksesta – tämän menetelmän käyttäminen on helpompaa kuin sen matemaattisen perustan ymmärtäminen. Tätä artikkelia tutkiessani löysin minkä tahansa määrän vastauksia opiskelijoiden kyselyihin, jotka olivat niin monimutkaisia, että ne eivät mitenkään voineet valaista opiskelijaa. Tässä artikkelissa teen kaikkeni tehdäkseni menetelmästä mahdollisimman yksinkertaisen ja helposti lähestyttävän.

Menetelmä on helpoin ilmaista algoritmina:

• Epäsäännöllisen monikulmion kärjet voidaan esittää kartesiokoordinaatteina: $x,y$.
• Jokaista koordinaattiparia käsitellään pinta-alan summausalgoritmissa, joka näyttää seuraavalta:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Yksinkertainen matemaattinen lauseke edellä mainitulle olisi:
  

  (2) Epäsäännöllisen monikulmion pinta-ala $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \kertoja y_i – y_{i+1} Jäljempänä selitettävissä tarkoituksissani tämä muoto on tarkoituksellinen – maanmittauksessa kenttätietojen pitäisi sulkea luku, eli viimeisen kohteen pitäisi vastata ensimmäistä. Tällaisessa sovelluksessa kuvion automaattinen sulkeminen yhtälön (1) mukaisesti kätkisi sisäänsä virheitä, jotka on arvioitava.

  Käyttäjät saattavat suosia yllä olevassa yhtälössä (1) esitettyä muotoa muihin tarkoituksiin kuin maanmittaustietojen vähentämiseen. Näitä tarkoituksia varten käsittelyn aikana yksinkertaisesti arvotetaan uudelleen ensimmäinen tietoerä läpikäynnin lopussa tai annetaan tietokokonaisuuksia, joissa ensimmäinen tietoerä toistuu viimeisenä.

• Tässä on täydellinen, toimiva Python-funktio:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• Ylläoleva ”array”-argumentti on joukko kartesiolaisia $x,y$-koordinaatteja, i.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Huomaa tästä datajoukosta, että ensimmäinen tieto toistuu lopussa.

• Tässä on hieman monimutkaisempi Python-funktio, joka laskee sekä pinta-alan että kehän pituuden:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Tämä muistutus taas: Molemmissa edellä mainituissa koodiesimerkeissä muissa sovelluksissa kuin maanmittaustietojen redusoinnissa toimitetun datasarjan tulisi sisältää kopio ensimmäisestä tietoerästä viimeisenä, i.eli luku pitäisi olla nimenomaisesti suljettu.

• Valitsin näissä esimerkeissä Pythonin, koska Python-listaus maksimoi algoritmisen merkityksen ja minimoi cruftin.

• Ylläolevat funktiot voidaan helposti muuntaa muille kielille, melkeinpä suoraan – lukuun ottamatta yllä esiteltyä kehän yhteenlaskemista, jossa hyödynnetään sitä, että Python tukee kompleksilukuja. Kielille, jotka eivät tue kompleksilukuja, voidaan luoda kehän tulos näin:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formallisesti kehän pituus on vektorien suuruuksien summa:
  

  (3) Kehän pituus $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}-y_i)^2}}$

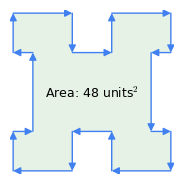
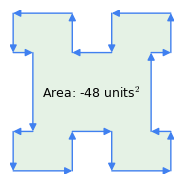Kuva 1: Kellon ympäri vs. vastapäivään vektorit

Tässä on joitakin tämän menetelmän tärkeitä ominaisuuksia:

• monikulmion sisällä valitulla alkupisteellä ei ole merkitystä pinta-alan tai ympärysmitan laskennan kannalta, ainoastaan sillä, että hahmo on suljettu, eli.eli viimeisen koordinaatin on oltava yhtä suuri kuin ensimmäisen koordinaatin.
• ”myötäpäiväsääntö”: vektoreiden järjestyksellä on merkitystä – jos kehä kuljetaan myötäpäivään, pinta-alan tulos on positiivinen, jos vastapäivään, se on negatiivinen (kuva 1). Juuri tämä menetelmän ominaisuus vähentää taivutusten pinta-alan monimutkaisesta kuviosta kuten kuvassa 1 – ”taivutukset” edustavat vastapäivään tapahtuvaa kulkua monikulmion sisällä.
• Monissa tämän menetelmän sovelluksissa käytetään alkuperäisiä tietolähteitä, jotka koostuvat polaarivektoreista (esimerkkinä maanmittauslaitoksen lailliset kuvaukset), mutta tämä menetelmä vaatii kartesiankoordinaatit. Muuntelu polaarikoordinaateista kartesiankoordinaatteihin on triviaalia, mutta on tärkeää pitää tämä vaatimus mielessä.
• Tarkan pinta-alalaskennan vuoksi kuvatun monikulmion on oltava suljettu kuvio – viimeisen koordinaatin on oltava yhtä suuri kuin ensimmäisen koordinaatin. Sovelluksissa, joissa käytetään kenttätietoja, jotka koostuvat pituusvektoreista, jotka jälkikäteen muunnetaan kartesiittiseen muotoon, on hyvä idea verrata alku- ja loppukoordinaatteja kartesiittiseen muotoon – niiden pitäisi olla samat. Esimerkiksi vanhemmat maanmittaukset (ennen halvan tietokonetehon aikakautta) epäonnistuvat säännöllisesti tässä testissä.

Tämä osio on täysin toimintakykyinen pinta-ala-/perimittaritietokone, joka pystyy käsittelemään syötettyjä kartesiolaisia tai polaarikoordinaattitietopareja tai maanmittauksen lainopillisia kuvauksia. Valitse vain tietotyyppi (kartesialaiset x,y-koordinaatit, polaariset m,θ-koordinaatit tai maanmittauksen oikeudellinen kuvaus) ja syötä (tai liitä) tiedot alla olevaan tietojen syöttöalueeseen. Voit myös valita esimerkkitietoaineistoja tutustumista ja harjoittelua varten.

Selaimen tietoturvaongelmien vuoksi lukijoiden on käytettävä järjestelmän leikepöytää liiallisen kirjoittamisen välttämiseksi ja merkittävien tietomäärien tuomiseksi toisesta lähteestä. Kopioi vain tiedot leikepöydälle lähdesovelluksessa, napsauta sitten alla olevaa tietojen syöttöaluetta ja paina Crtl+A valitaksesi kaikki, Ctrl+V poistaaksesi tietoja muualta ja Ctrl+C kopioidaksesi omat syötetyt tietosi. Useimmissa selaimissa on leikepöytätoiminnot myös valikkokohteina.

Valitse tietotyyppi:

Kartesiallinen (x,y)

polaarinen (m,θ)

Maanmittauskuvaus

Tietojen syöttöalue: Valitse kaikki: Ctrl+A | Kopioi: Ctrl+C | Liitä: Ctrl+V

Kaavioalue:

Pahoittelemme – selaimesi ei tue tämän ominaisuuden vaatimaa graafista kykyä –
harkitse Google Chromen tai Firefoxin asentamista.

Valinnat:

Viivat

Nuolet

Alkupiste

Keskipiste

Pituusyksikkö:

Viivan leveys:

Käänteinen

Tulokset: Valitse kaikki: Valitse kaikki: Ctrl+A | Kopioi: Ctrl+C | Liitä: Ctrl+V

Pinta-ala-/perimetritietokoneessa on kolme syöttötilaa:

• Kartesiolaiset (x,y) koordinaattiparit:

  • Jokainen koordinaatti on kaksiulotteinen sijainti, jossa on vaakasuora (x) ja pystysuora (y) osa (kartesiankoordinaatti).
  • Koordinaatit eivät ole kumulatiivisia – kukin kuvaa itsenäisesti sijaintiaan.
  • Siten neliö olisi:
    • 0,0 (origo)
    • 0,100 (ylös)
    • 100,100 (oikealle)
    • 100,0 (alas)
    • 0,0 (takaisin origoon)
  

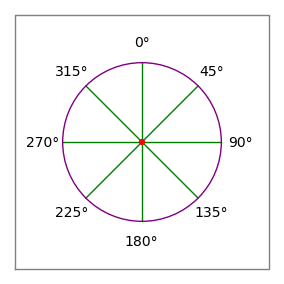  Avio 2: Kompassiruusu

  • Yllä olevan esimerkin pilkut on tarkoitettu vain ryhmittelemään tietopareja lukijaa varten – niillä ei ole mitään merkitystä aluetietokoneen tietojen jäsentäjälle.
  • Parseri on sen verran vankka, että yllä olevan esimerkin voi liittää tietokoneen tietojen syöttöalueelle ja se toimii (kokeile).
  • Ainut rajoitus on, että selittävät kommentit eivät voi sisältää numeroita.

• Polaariset (m,θ) koordinaattiparit:

  • Jokainen koordinaatti koostuu etäisyydestä ja kulmasta asteina (polaarinen vektori).
  • Kulmat noudattavat kompassikonventiota – 0 astetta on ylöspäin eli ”pohjoiseen”, 90 astetta on oikealle eli ”itään” (kuva 2).
  • Toisin kuin aiempi kartesiolaismuoto, nämä koordinaatit ovat kumulatiivisia – kukin uusi vektori lisää tämänhetkistä sijaintia.
  • Neliö olisi siis:
    • 100,0 (ylös)
    • 100,90 (oikealle)
    • 100,180 (alas)
    • 100,270 (takaisin alkupisteeseen)
  • Kuten aiemminkin, tämä esimerkki toimii, jos se liimataan tietokoneen tietojen syöttöalueelle ja valitaan polaarinen tila.
  • Huomaa polaarikoordinaateista, että origo on implisiittinen ja esiasetettu arvoon x = 0, y = 0.
  

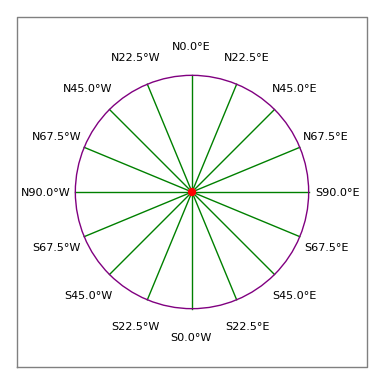  Kuvio 3: Maanmittarin kompassiruusu

• Lainmukainen kuvaus:

  • Aluksi selitys ”Pituusyksiköt”-valinnan ja tulosnäytön välisestä suhteesta:
    • Kullekin polygonille lasketaan luettelo pinta-alatuloksista käyttäen kiinteää joukkoa yleisiä pinta-alayksiköitä (jalkaa2, metriä2 jne.). Jotta tämä pinta-alaluettelo olisi mielekäs, syötetyt pituusyksiköt on tunnettava.
    • Kartesiallisessa ja polaarisessa tilassa tietueilla ei ole yksiköitä, joten käyttäjä valitsee, mitä yksiköitä pituuksille annetaan. Kun käyttäjä siis vaihtaa pituusyksiköitä, pinta-alan arvot muuttuvat, pituusmerkinnät muuttuvat, mutta pituusarvot eivät.
    • Mittaustilassa oikeudellinen kuvaus sisältää pituusyksiköt (jalat, metrit jne.), mikä tarkoittaa, että pituusyksiköt ovat lähteen ennalta määrittelemiä. Kun käyttäjä siis muuttaa pituusyksiköitä, tämä muuttaa pituusmerkintöjä ja -arvoja, ei pinta-ala-arvoja.
  • Kartoituskuvauksen jäsentäjä on ylivoimaisesti epäluotettavin kolmesta tietojen jäsentämismenetelmästä – se on enemmänkin kokeilu kuin vankka tietojen muuntamismenetelmä.
  • Kirjoitin tämän jäsentäjän lataamalla useita lakisääteisiä kuvauksia (jotka on annettu esimerkkeinä yllä olevassa laskurissa) ja virittämällä jäsentäjän koodia, kunnes kaikki voitiin onnistuneesti purkaa.

  ”Onnistumisen” kriteerit olivat, että tuloksessa olisi sama neliöala kuin kuvauksen väittämissä, ja että luku olisi ”lähellä”.

  • Termiä ”sulkeutuminen”, ja erityisesti sulkeutumisvirhe, käytetään maanmittaustöissä kuvaamaan sitä, missä määrin maanmittauksen loppupiste vastaa alkupistettä. Tämä pitää harvoin paikkansa todellisuudessa – sulkeutumisvirheet johtuvat yleensä kenttätyön virheistä, ja vanhemmissa kartoituksissa, jotka on julkaistu ennen halpojen tietokoneiden tuloa, sulkeutumisvirheet ovat yleensä melko huonoja ja neliöalojen arviot ovat hyvin epätarkkoja.
  • Kartoituksen laillinen kuvaus on muodollinen tapa kuvata tontti – sen muoto ja syntaksi on syntynyt vuosikymmenten aikana maanmittareiden yhteisesti hyväksymien, jokseenkin mielivaltaisten ja yhteisten konventioiden avulla.
  • Tässä pinta-ala/ympyräkohta-tietokoneessa syötettävien tietojen on noudatettava tiettyjä tiukkoja konventioita, joita jotkin lailliset kuvaukset noudattavat, mutta eivät kaikki. Olennaiset elementit ovat seuraavat:
    • Esiintyy ilmaisu ”alkupiste”, joka erottaa osan alustavasta sisällöstä siitä sisällöstä, joka kuvaa kuvattavan lohkon mittoja. Joissakin asiakirjoissa sanotaan ”Todellinen alkupiste”, joissakin ”Todellinen alkupiste” ja joissakin ”Alkupiste”. Onnistuneen jäsentäjän on poistettava tätä lausetta edeltävä sisältö ja säilytettävä kaikki sen jälkeinen sisältö.
    • Sarja lauseita, jotka kuvaavat maanmittareiden käyttämää erityyppistä napavektoria:
      • Sana ”North” tai ”South” tai sen lyhenne ”N” tai ”S”.
      • Seuraava kulma ilmaistuna asteina, minuutteina ja sekunteina.
      • Seuraava sana ”East” tai ”West” tai sen lyhenne ”E” tai ”W”.
      • Sitten etäisyys.
      • Sitten etäisyysyksikkö – jalat, metrit jne.
  • Tässä on joitain erilaisia esimerkkejä maanmittausvektoreista oikeudellisista esimerkkikuvauksista:
    • N 2°0’0″ W – 63.50 feet
    • N90°00’00 ”W ALONG A LINE PARALLEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.86 jalkaa
    • S. 22 astetta 41′ 55″ E. 174.10 jalkaa
  • Huomaa yllä olevista esimerkeistä, että niissä kaikissa on erilainen syntaksi. On olemassa monia oikeudellisia kuvauksia, joita tämä jäsentäjä ei onnistu purkamaan, vain siksi, että en ole yrittänyt sisällyttää niiden syntaksia. On kuitenkin tärkeää lisätä, että todella vankan jäsentäjän, joka soveltuisi lukuisiin olemassa oleviin oikeudellisiin kuvauksiin, pitäisi olla yhtä älykäs kuin Watson.
  • Tämän alue/alue- ja kehätietokoneen käyttäjät voivat välttää lähettämästä pelkkiä oikeudellisia kuvauksia ja toivoa, että jäsentäjä selvittää ne. Jos haluat tehdä suoria käsin tehtäviä merkintöjä (tai luoda luettelon muualta tuotavista traversseista), käytä tätä konventiota:
    • Muista, että hyväksyttävä traverssimerkintä koostuu sanasta ”North” (pohjoinen) tai ”South” (etelä) tai kirjaimesta ”N” (N) tai ”S” (S), jota seuraa enintään kolme numeroa, jotka ilmoittavat kulman asteet, minuutit ja sekunnit, jota seuraa sana ”East” (itä) tai ”West” (länsi) tai kirjain ”E” (E) tai ”W” (W), jota seuraa välimatka ja sen jälkeen välimatkayksikkö.
    • Kelpoinen merkintä olisi siis ”N 30 15 45 W 100 jalkaa”, joka tarkoittaa 100 jalan pituista poikkileikkausta, joka osoittaa 30 astetta, 15 minuuttia ja 45 sekuntia pohjoisen länsipuolelle (eli suunnilleen 330 kompassiastetta, ks. kuva 3).
    • Minuutti- ja sekuntimerkinnät voidaan ohittaa, jos ne ovat nolla tai jos merkintä on tehty desimaaliasteina tai asteina ja desimaaliminuutteina.
  • Painetun oikeudellisen kuvauksen muuntaminen tällaisiksi merkinnöiksi ei ole vaikeaa, ja virheiden havaitsemiseen on useita tapoja. Kun kaikki poikkileikkaukset on syötetty, jos kuviossa ei ole sulkuvirheitä ja se ilmoittaa saman neliöalan kuin alkuperäinen, on todennäköistä, että merkinnät ovat oikeita (tai niissä on samat virheet kuin alkuperäisessä kuvauksessa).
  • Kun olet syöttänyt oikeudellisen kuvauksen tällä tavoin, jos sulkuvirheitä ei voida hyväksyä tai neliöala on väärä, muista, että alkuperäiset tiedot saattavat olla virheellisiä. On olemassa mitä tahansa määrää oikeudellisia kuvauksia, joita ei ole koskaan tarkistettu tällaisella tietokonemenetelmällä ja jotka eivät ole koskaan olleet oikeita.

Kartesiolaisia (x,y)-esimerkkejä selaillessasi huomaa erilaisten muotojen pinta-alan ja ympärysmitan suhde. ”Omituisen muotoisella monikulmiolla” on keskimmäinen suhde, ympyrällä on pienin suhde, ja Hilbertin avaruudella on ylivoimaisesti suurin suhde. Tämä suhde ulottuu korkeampiin ulottuvuuksiin, joissa pallolla tiedetään olevan suurin tilavuus pinta-alaa kohti.

Ympyräesimerkistä – se on ”yksikköympyrä”, ympyrä, jonka säde on yksi. Annetussa esimerkissä pinta-ala on likimain $\pi$ ja ympärysmitta likimain $2\pi$, jotka ovat oikeat arvot yksikköympyrälle. Jotta nämä arvot olisivat enemmän kuin approksimaatioita, jotta ne olisivat täsmälleen yhtä suuret $\pi$ ja $2\pi$, monikulmion sivujen lukumäärän pitäisi olla ääretön. Päätin vastustaa tätä. 🙂

Hilbert-avaruuden esimerkki luotiin käyttäen Sagen algoritmia, jonka järjestysvalinta oli vaatimaton (jotta vältyttäisiin tuottamasta liikaa dataa). Periaatteessa Hilbert-avaruudella voi olla ääretön kehän ja pinta-alan suhde kahdessa ulottuvuudessa tai pinta-alan ja tilavuuden suhde kolmessa ulottuvuudessa. Jos haluat nähdä, kuinka monimutkaiseksi Hilbert-avaruus voi muuttua, klikkaa tästä nähdäksesi järjestyksen 7 Hilbert-avaruuden.

Huomaa Hilbert-esimerkistä, että laskettu pinta-ala on lähellä 1/2 1×1-pinnalle. Ihannetapauksessa, ilman tarvetta muuntaa viivakuvio pinta-alaluvuksi ja oikealla algoritmilla, pinta-ala olisi täsmälleen 1/2 samanmittaisen neliön pinta-alasta.

Polaarinen syöttötila vastaa suurin piirtein Turtle-grafiikkaa, jos ”ylös” korvataan nollalla asteella, ”oikealle” 90 asteella jne. ja jos kukin kääntö- ja siirtosekvenssi tiivistetään yhdeksi komennoksi. Polaarisen syöttötilan käyttäminen on helppo tapa rakentaa monimutkainen muoto käsin, koska etäisyyksiä ja kulmia on helpompi seurata kuin kartesiankoordinaatteja.

Käytin edellä kuvattua maanmittausalueen laskentamenetelmää ensimmäisen kerran vuosia sitten asuessani Oregonin maaseudulla, jossa asui ihmisiä, jotka tarvitsivat tietää kiinteistöjensä pinta-alan ja kehän. Törmäsin moniin järkyttäviin esimerkkeihin, joissa kiinteistönvälittäjät röyhkeästi huijasivat ihmisiä, joilla ei ollut mitään keinoa saada selville, mistä oli kyse. Laskin useaan otteeseen pinta-alan oikeudellisen kuvauksen perusteella vain havaitakseni, että takuukirjan pinta-alaa koskeva väite oli täysin epätarkka – ja aina todellisuutta suurempi.

Eräässä tapauksessa minua pyydettiin jakamaan kiinteistö kahteen yhtä suureen osaan ja laatimaan oikeudelliset kuvaukset kummallekin. Koska minulla oli vastikään hankittu Apple II (jossa oli nykyaikaisen kynänteroittimen prosessointiteho), tämä oli hyvin helppoa – mutta työskennellessäni huomasin, että kokonaispinta-ala oli noin kolme eekkeriä, noin 25 prosenttia kokonaispinta-alasta, pielessä. Otin asian puheeksi omistusoikeusyhtiön kanssa, joka vastasi röyhkeästi: ”Näetkö tässä, missä kauppakirjassa sanotaan ’enemmän tai vähemmän’?”

Toisen kerran aloitin maa-alueen oston, mutta edellä mainitun kokemuksen varoittamana, kun sain omistusoikeuskirjan, päätin syöttää sen juridisen kuvauksen ohjelmaani nähdäkseni, oliko pinta-alaa koskeva väite oikea. Mutta kauhukseni huomasin, että kaikissa kyseisen osaston lohkojen omistusoikeuskirjoissa oli sama oikeudellinen kuvaus – ensimmäisenä mitatun kiinteistön oikeudellinen kuvaus. Kävi ilmi, että maanrakennusyhtiö oli päättänyt säästää rahaa kartoittamalla vain yhden kymmenistä myytäväksi tarjotuista tonteista ja sisällyttämällä tämän oikeudellisen kuvauksen kaikkiin omistusoikeuskirjoihin. He olivat varmoja, että he pääsisivät siitä pälkähästä – kuka loppujen lopuksi tietää mitään matematiikasta?

Kiisteltyäni omistusoikeusyhtiön ja rakennuttajan kanssa ja yritettyäni taivutella heitä maksamaan maanmittauksista, jotta lailliset kuvaukset eivät olisi kohteliaita fiktioita, luovutin ja päätin olla ostamatta maata. Se oli kuin selvittäisi, miten makkaraa valmistetaan – on mahdollista tietää liikaa.

• 04.15.2013 Versio 1.3. Lisätty yksityiskohtainen selitys oletusdatamuodosta, eli listoista, jotka toistavat ensimmäisen datapisteen viimeisenä.
• 03.24.2013 Versio 1.2. Kyselyn kuvauksen jäsentäjää optimoitu edelleen, lisätty lisää tulostietokenttiä.
• 03.23.2013 Versio 1.1. Parannettu oikeudellisen kuvauksen jäsentäjää käsittelemään useampia kuvaustyyppejä, lisätty pituusyksiköiden valitsin ja tulosluettelo alueista yleisissä yksiköissä.
• 03.22.2013 Versio 1.0. Ensimmäinen julkinen julkaisu.