Tämän päivän postauksessa opit eron prime- ja komposiittilukujen välillä. Lisäksi näytämme useita esimerkkejä, jotka auttavat sinua ymmärtämään niitä paremmin.
Index
Mitä ovat alkuluvut?
Primiluvut ovat lukuja, jotka ovat jaollisia vain itsellään ja 1:llä, eli jos yritämme jakaa ne jollakin muulla luvulla, tulos ei ole kokonainen luku. Jos siis jaat luvun jollain muulla kuin ykkösellä tai itsellään, saat jäännöksen, joka ei ole nolla.
Primaluvut 100:aan asti
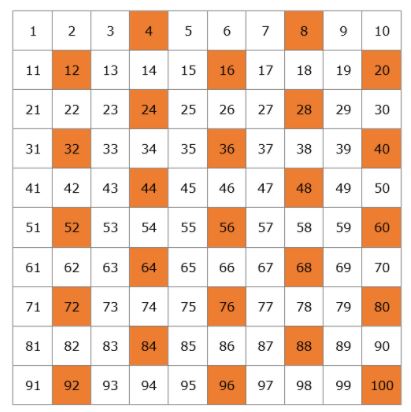
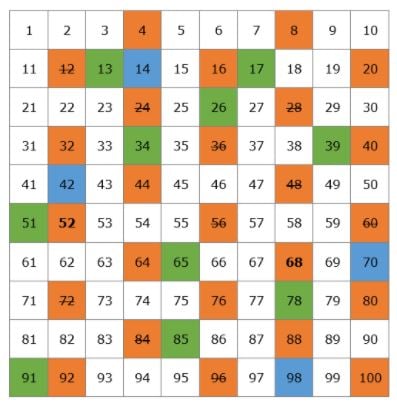
Luomme taulukon, jossa on kaikki primaluvut, jotka ovat olemassa 100:aan asti.
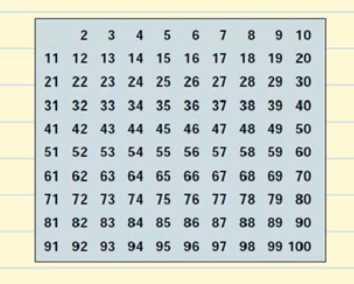
Aloitetaan luvusta 2. 2 on alkuluku, mutta kaikki 2:n kertaluvut ovat yhdistettyjä lukuja, koska ne ovat jaollisia 2:lla. Poistetaan taulukosta kaikki 2:n kertaluvut.
Seuraava alkuluku on 3, joten voimme yliviivata kaikki 3:n kertaluvut, koska ne ovat yhdistettyjä lukuja.
3:n jälkeen on seuraava alkuluku 5, joten yliviivaamme kaikki 5:n kertaluvut.
Sitten on alkuluku 7 ja yliviivaamme kaikki 7:n kertaluvut.
Seuraava alkuluku on 11, joten yliviivaamme kaikki 11:n kertaluvut, jotka ovat 22, 33, 44, 55, 66, 77, 88 ja 99. Kaikki nämä luvut olimme jo yliviivanneet, joten olemme saaneet valmiiksi kaikkien taulukkomme yhdistelmälukujen yliviivaamisen.

Tässä on listamme alkuluvuista 1-100. Sinun ei tarvitse opetella niitä ulkoa, mutta olisi parasta, jos muistaisit pienemmät luvut, kuten 2, 3, 5, 7, 11, 13.
Kuinka monta alkulukua on olemassa?
Kreikkalainen matemaatikko Eratosthenes (3. vuosisata eaa.) suunnitteli nopean tavan löytää kaikki alkuluvut mihin tahansa numeroon asti. Menetelmää kutsutaan Eratostenesin seulaksi.
Huomaa, että 1:n ja 100:n välillä on 25 alkulukua. Kuinka monta alkulukua on yhteensä? Olemme jo antiikin ajoista lähtien tienneet, että niitä on ääretön määrä, joten on mahdotonta luetella niitä kaikkia. Koska Eukleides, joka ensimmäisenä osoitti 4. vuosisadalla eaa., että niitä on ääretön määrä, ei tuntenut äärettömyyden käsitettä, hän sanoi, että ”alkulukuja on enemmän kuin mikä tahansa kiinteä määrä niitä”, mikä tarkoittaa, että jos kuvittelet 100, niitä on enemmän, ja jos kuvittelet miljoona, niitä on vieläkin enemmän.
Alkuluvut 100:sta 1000:een
Katsotaan alkulukuja 100:sta 1000:een.

Olemme pahoillamme, ettemme voi näyttää niitä kaikkia, sillä kuten tiedät, niitä on ääretön määrä. 😉
Primaluvut Esimerkkejä
Voidaksemme auttaa sinua ymmärtämään paremmin primalukuja selitämme harjoituksen.
Saralla on 6 karkkia, jotka hän haluaa jakaa, mutta hän ei tiedä, kuinka monelle ihmiselle hän voi jakaa ne niin, että kaikki saavat saman määrän eikä yhtään jää yli. Kuinka monella tavalla hän voi tehdä tämän?
Tässä on Sara ja hänen 6 karkkipalaansa:

Miten karkit voidaan jakaa?
Ensimmäinen ja helpoin tapa on antaa ne yhdelle henkilölle, eli jakaa ne 1:llä. Näin tämä henkilö saa 6 karkkia.
Seuraava mahdollisuus on jakaa ne 2 henkilön kesken. Koska 6 jaettuna 2:lla on 3, jokainen henkilö saa 3 karkkia!

Jatketaan seuraavalla luvulla, 3. Jos jaamme 6 karkkia 3 henkilön kesken, sekin on tarkka jako, ja jokainen henkilö saa 2 karkkia:

Jatketaan numeroiden kanssa. Meillä ei ole tarkkoja jakoja 4:n ja 5:n kanssa, mutta 6:n kanssa on.
Koska 6 jaettuna 6:lla on 1, voimme antaa 6 lapselle kullekin 1 karkin.

Keräämme joitakin tietoja. Meillä on 6 karkkia, jotka voimme jakaa (tarkalla jaolla) 1, 2, 3 ja 6 ihmisen kesken. Toisin sanoen voimme jakaa luvun 6 ja saada jäännökseksi 0, kun jaamme sen luvulla 1, 2, 3 ja 6. Näitä lukuja kutsutaan 6:n jakajiksi.
Kokeillaan toisella luvulla, esimerkiksi 7:llä.
Nyt Saralla on 7 karkkia ja hän haluaa jakaa ne, mutta hän ei tiedä, kuinka monelle ihmiselle hän voi jakaa karkkeja niin, että kaikki saavat saman verran eikä yhtään jää yli. Kuinka monella tavalla hän voi tehdä tämän?

Henry on niin onnekas! Hän sai kaikki karkkipalat!
Onko muita tapoja tehdä se? Emme voi jakaa 7:ää 2:lla, 3:lla, 4:llä, 5:llä tai 6:lla, …mutta 7:n jakaminen on mahdollista!
Sara voi jakaa karkkipalat 7:n kesken antamalla kullekin yhden karkkipalan:

Seuraavasti 7:n voi jakaa vain 1:llä ja 7:llä, sen ainoat jakajajoukot ovat 1:n ja 7:n. Tällaisia lukuja kutsumme alkuluvuiksi.
Onko muitakin alkulukuja? Totta kai! Etsitäänpä niitä lisää:
- Onko 4? Ei! Koska sen jakajat ovat 1, 2 ja 4.
- Onko 5? Kyllä! Koska sen jakajat ovat 1 ja 5.
- Onko 8? Ei! Koska sen jakajat ovat 1, 2, 4 ja 8.
Lyhyesti sanottuna luku on alkuluku, jos sillä on vain kaksi jakajaa: 1 ja oma itsensä.
Nyt voit etsiä paljon alkulukuja!
Miten löytää alkulukuja
Katso tarkasti! Annamme sinulle tempun, jolla voit tietää, onko luku alkuluku vai ei, ilman että sinun tarvitsee etsiä sen jakajia, mutta tavalla, joka on hauskempi ja antaa meille jakajat (jos niitä on).
Valitaan satunnainen luku, esimerkiksi 16.
Tarkistaaksemme, onko se alkuluku vai ei, käytämme taulukkoa, joka on hyvin samankaltainen kuin Montessori-kortit kertolaskuun. Ja saamme niin monta palloa kuin valitsemamme luku on. Tässä tapauksessa 16 palloa.
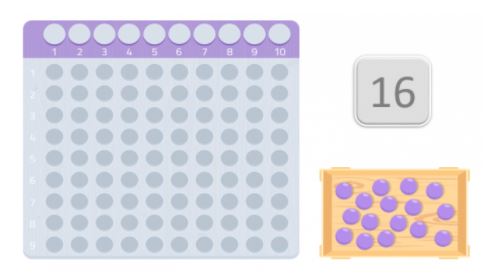
Kun meillä on taulukko ja pallot, meidän on asetettava ne pöydälle aloittaen ensimmäisestä tilasta ja yritettävä muodostaa suorakulmio. Luvut, jotka muodostavat suorakulmion reunat, ovat kyseisen luvun jakajia.
Jos onnistumme muodostamaan suorakulmion vain käyttämällä samaa lukua, jota käytämme, ja lukua 1, se on alkuluku.
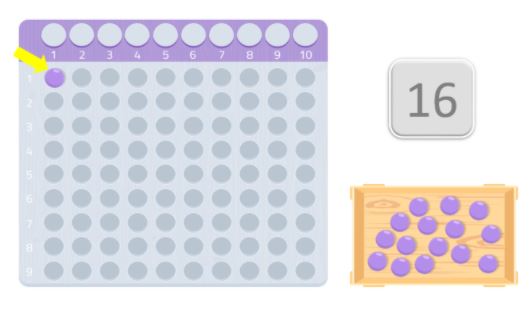
Esimerkiksi tässä tapauksessa asetamme ensimmäiselle riville 8 palloa ja toiselle riville vielä 8 palloa. Kuten näet, olemme muodostaneet suorakulmion ja voimme nähdä, että 8, kuten 2, ovat luvun 16 jakajia. Siksi 16 ei ole alkuluku, koska kuten tiedät, alkuluvut ovat sellaisia, jotka ovat jaollisia vain itsellään ja 1:llä.
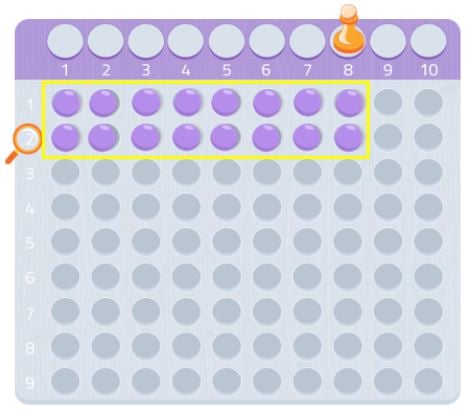
Voidaan kokeilla toisella luvulla, esimerkiksi 7:llä.
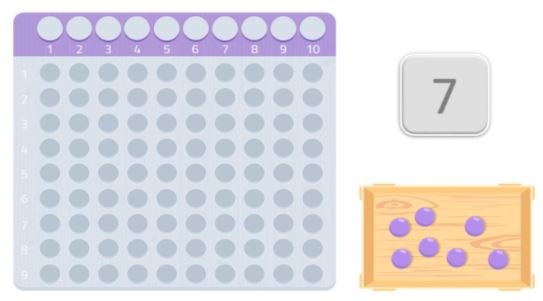
Kuten näemme, emme voisi tehdä täyttä suorakulmiota, meiltä puuttuisi yksi pallo. Koska emme pysty muodostamaan suorakulmiota, voimme sanoa, että luvulla 7 ei ole muita jakajia kuin se itse ja 1, kuten näemme seuraavasta kuvasta.
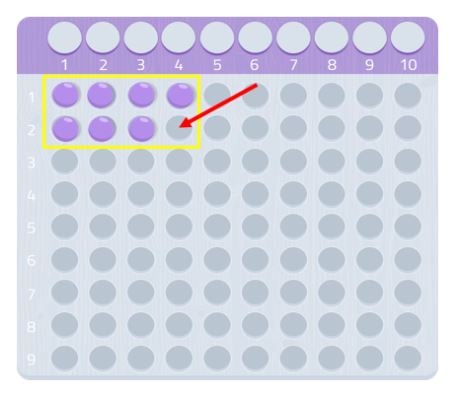
Siten 7 on alkuluku!
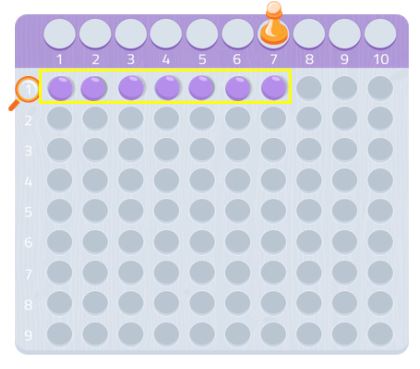
Kokeile mitä tahansa muuta lukua, niin näet, miten se toimii! Voit käyttää kuvaajapaperia ja etsiä suorakulmioita, joissa on kyseinen määrä neliöitä.
Miksi alkuluvut ovat tärkeitä?
Primiluvut ovat avain aritmetiikkaan, alla näet esimerkin, joka osoittaa niiden tärkeyden paitsi matematiikassa myös luonnossa.
Mitä tarkoitamme, kun sanomme, että primiluvut ovat avain aritmetiikkaan?
Se johtuu siitä, että mikä tahansa luku koostuu ainutlaatuisesta tuotteesta, joka muodostuu näiden lukujen sarjasta.
Es uskotaan, että niitä on tutkittu noin 20 000 vuoden ajan, kun esi-isämme kirjoitti sarjan alkulukuja (11, 13, 17 ja 19) Ishangon luuhun. Ikään kuin tämä olisi sattumaa, on vahvistettu, että muinaiset egyptiläiset työskentelivät niiden parissa 4 000 vuotta sitten.
Lisäksi luonto tuntee ne hyvin, ja jotkut lajit ovat pystyneet löytämään ne koko evoluutionsa ajan ja käyttäneet niitä hyväkseen selviytyäkseen.
Viittaan useisiin sirkkalajeihin, kuten Pohjois-Amerikassa elävään Magicicada septendeciumiin. Tämä sikada-laji on vakiinnuttanut lisääntymiskiertonsa noin 13 tai 17 vuodeksi, ei 12, 14, 15, 16 tai 18 – tasan 13 tai 17. Näin ne pystyvät välttämään saalistajia, joilla on myös jaksoittainen lisääntymissykli; kuvittele saalistajaa, jolla on nelivuotinen lisääntymissykli.
Jos sirkan elinkaari olisi 12 tai 14 vuotta, se osuisi saalistajan kanssa samaan aikaan hyvin usein, paljon useammin kuin jos elinkaari olisi 13 tai 17 vuotta. Tasan 2 kertaa sadan vuoden välein, kun taas muuten ne osuisivat yhteen 11 syklissä, mikä vaarantaisi lajin kehityksen.
Sähköisen viestinnän turvallisuus perustuu myös alkulukuihin. Jokaiseen salattuun viestiin, joka lähetetään internetissä (viestiverkoissa, ostoksissa tai sähköisessä pankkiasioinnissa), liittyy jokin suurluku, ja on hyvin vaikea tietää, onko se alkuluku vai ei. Vastaanottajalla on yksi sen jakaja, ja siksi hän voi purkaa salauksen. Primuslukujen olemassaolo on siis kriittistä yksityisyytemme kannalta, kun kommunikoimme sähköisesti.
Mitä ovat yhdistetyt luvut?
Komposiittiluvut ovat lukuja, jotka ovat jaollisia 1:llä ja itsellään sekä muilla luvuilla.
Katsomme esimerkin alkuluvusta ja komposiittiluvusta.
11 voidaan kirjoittaa kertolaskuna 1 x 11, mutta sitä ei voida kirjoittaa muuna luonnollisten lukujen kertolaskuna. Sillä on vain jakajat 1 ja 11, ja siksi se on alkuluku.
12 voidaan kirjoittaa kertolaskuna 1 x 12 sekä kertolaskuna 3 x 4 ja 2 x 6. Koska 12 on jaollinen useammalla luvulla kuin 1:llä ja itsellään, 12 on yhdistetty luku.
Onko 1 alkuluku?
On ihmisiä, jotka uskovat niin, koska he sanovat, että 1 voidaan jakaa vain 1:llä ja itsellään, mutta matematiikassa luku 1 on hylätty alkulukuna, koska sillä on vain yksi jakaja. Itse asiassa kriteeriä ”positiivinen kokonaisluku on alkuluku, jos sillä on täsmälleen kaksi positiivista jakajaa” käytetään jättämään luku 1 pois alkulukujen listalta. Tämä ei johdu siitä, että olisimme nirsoilevia, mutta jos lukua yksi pidettäisiin alkulukuna, niin monet matemaattiset ominaisuudet olisi sanottava toisin.
Niin, 1 on siis komposiittiluku?
Noh, se ei myöskään ole komposiittiluku, koska sitä ei voi laittaa alkulukujen tuloksi. Luku 1 ei ole alkuluku eikä komposiittiluku. Ja ennen kuin kysyt, nollakaan ei ole alkuluku eikä komposiittiluku, mutta tämä johtuu siitä, että kaikki ne seikat, jotka selitimme positiivisille luvuille eli nollaa suuremmille luvuille.
Luvun jakaja
Luvun jakaja on arvo, joka jakaa luvun täsmällisiin osiin, toisin sanoen jäännös on 0.
Laskemme esimerkkinä 24:n jakajat.
Aloitamme jakamisen pienimmistä luvuista alkaen numerosta 1.
- 24 / 1 = 24. Sekä 1 että 24 ovat jakajia.
- 24 / 2 = 12. Eli 2 ja 12 ovat jakajia.
- 24 / 3 = 8. Eli 3 ja 8 ovat jakajia.
- 24 / 4 = 6. Eli 4 ja 6 ovat jakajia.
- 24 / 5 = 4. Eli 4 ja 6 ovat jakajia. Se ei ole tarkka jakolasku ja jäännös on 4, joten 5 ei ole jakaja.
Seuraava luku on 6, mutta koska tiedämme jo, että 6 on 24:n jakaja, olemme saaneet valmiiksi 24:n jakajien laskemisen.
Video: Faktorisointi ja alkuluvut
Jos haluat tietää lisää alkuluvuista ja yhdistelmäluvuista, katso seuraava video. Opit myös faktoroinnin käsitteen Montessori-taulukon avulla.
Tämä video on yksi interaktiivisista opetusohjelmistamme, ja vaikka se ei olekaan interaktiivinen, voit silti katsoa sen niin monta kertaa kuin haluat ja jakaa sen ystävien kanssa. Jos haluat käyttää interaktiivisia opetusohjelmiamme, rekisteröidy Smartickiin! Verkkomenetelmä, joka auttaa 4-14-vuotiaita lapsia oppimaan ja harjoittelemaan matematiikkaa.
Jos haluat jatkaa oppimista alkuluvuista ja parhaasta matematiikasta, joka on sovitettu tasollesi, rekisteröidy Smartickiin ja kokeile sitä ilmaiseksi!
Learn More:
- Ykkösluvut ja komposiittiluvut
- Ykkösluvut: A Trick to Help You Identify Them
- Prime Numbers:
- Learn How to Factor into Prime Numbers
- Prime Numbers Activities with Smartick



- Author
- Recent Posts
Matemaatikoista, opettajista, professoreista ja muista koulutuksen ammattilaisista koostuva monialainen ja monikulttuurinen tiimi!
Hän pyrkii luomaan parasta mahdollista matematiikan sisältöä.
- Esimerkkejä 3. luokan matemaattisista sanatehtävistä ja niiden ratkaisuista – 03/25/2021
- Peräkkäiset sisäkulmat: What They Are and How to Find Them With Examples – 03/11/2021
- Esimerkkejä toisen luokan sanaongelmista ratkaisuineen – 02/04/2021