Työnnettävässä nesteessä on potentiaalienergiaa (paineenkorkeus) ja liike-energiaa (nopeuskorkeus). Neste voi olla kokoonpuristuvaa tai kokoonpuristumatonta. Turbiinit käyttävät useita fysikaalisia periaatteita tämän energian keräämiseksi:
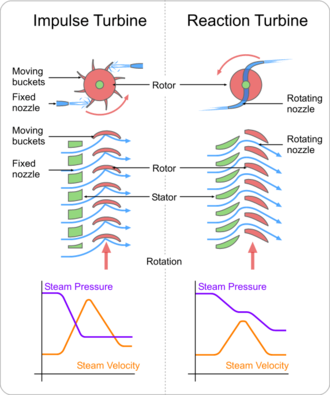
Impulssiturbiinit muuttavat suuren nopeuden nesteen tai kaasusuihkun virtaussuuntaa. Syntyvä impulssi pyörittää turbiinia ja jättää nestevirtauksen pienentyneellä liike-energialla. Nesteen tai kaasun paine ei muutu turbiinin siivissä (liikkuvissa siivissä), kuten höyry- tai kaasuturbiinissa, vaan kaikki paineen lasku tapahtuu paikallaan olevissa siivissä (suuttimissa). Ennen turbiiniin pääsyä nesteen painekorkeus muutetaan nopeuskorkeudeksi kiihdyttämällä nestettä suuttimella. Pelton-pyörissä ja de Laval -turbiineissa käytetään yksinomaan tätä prosessia. Impulssiturbiinit eivät vaadi roottorin ympärillä olevaa painekoteloa, koska suuttimella luodaan nestesuihku ennen roottorin lapojen saavuttamista. Newtonin toinen laki kuvaa impulssiturbiinien energiansiirtoa. Impulssiturbiinit ovat tehokkaimpia silloin, kun virtaus on pieni ja tulopaine korkea.
Reaktioturbiinit kehittävät vääntömomentin reagoimalla kaasun tai nesteen paineeseen tai massaan. Kaasun tai nesteen paine muuttuu, kun se kulkee turbiinin roottorin lapojen läpi. Työnesteen hillitsemiseksi tarvitaan painekotelo, kun se vaikuttaa turbiinin lapoihin, tai turbiini on upotettava kokonaan nestevirtaukseen (kuten tuuliturbiinissa). Kotelo sisältää ja ohjaa työstönestettä, ja vesiturbiinien osalta se ylläpitää vetoputken aiheuttamaa imua. Francis-turbiinit ja useimmat höyryturbiinit käyttävät tätä konseptia. Kokoonpuristuvissa nesteissä käytetään yleensä useita turbiinivaiheita paisuvan kaasun tehokkaan hyödyntämisen varmistamiseksi. Newtonin kolmas laki kuvaa energiansiirtoa reaktioturbiineissa. Reaktioturbiinit soveltuvat paremmin suuremmille virtausnopeuksille tai sovelluksiin, joissa nesteen virtauskorkeus (paine ylävirtaan) on alhainen.
Höyryturbiinien tapauksessa, jollaisia käytettäisiin esimerkiksi merenkulkusovelluksissa tai maalla tapahtuvassa sähköntuotannossa, Parsons-tyyppinen reaktioturbiini vaatisi suunnilleen kaksinkertaisen määrän siipirivejä de Laval -tyyppiseen impulssiturbiiniin verrattuna, jotta lämpöenergian muuntaminen olisi yhtä tehokasta. Vaikka tämä tekee Parsonsin turbiinista paljon pidemmän ja raskaamman, reaktioturbiinin kokonaishyötysuhde on hieman korkeampi kuin vastaavalla impulssiturbiinilla samalla lämpöenergiamuunnoksella.
Käytännössä nykyaikaisissa turbiinisuunnitelmissa käytetään sekä reaktio- että impulssiturbiinikonsepteja vaihtelevassa määrin aina kun se on mahdollista. Tuulivoimaloissa käytetään siipiprofiilia tuottamaan liikkuvasta nesteestä reaktiovoimaista nostetta ja siirtämään sitä roottoriin. Tuulivoimalat saavat jonkin verran energiaa myös tuulen impulssista poikkeuttamalla sitä kulmassa. Monivaiheisissa turbiineissa voidaan käyttää joko reaktio- tai impulssilaippoja korkeassa paineessa. Höyryturbiinit ovat perinteisesti olleet enemmän impulssiturbiinimoottoreita, mutta ne ovat edelleen siirtymässä kohti reaktiomalleja, jotka muistuttavat kaasuturbiineissa käytettyjä malleja. Matalassa paineessa väliaineena toimivan nesteen tilavuus laajenee pienellä paineen alenemisella. Näissä olosuhteissa siivekkeistä tulee puhtaasti reaktiotyyppisiä, ja siiven pohja on yksinomaan impulssityyppinen. Tämä johtuu kunkin siiven pyörimisnopeuden vaikutuksesta. Tilavuuden kasvaessa terän korkeus kasvaa, ja terän pohja pyörii hitaammin kuin kärki. Tämä nopeuden muutos pakottaa suunnittelijan vaihtamaan impulssin tyvestä korkean reaktion tyyliseen kärkeen.
Klassiset turbiinien suunnittelumenetelmät kehitettiin 1800-luvun puolivälissä. Vektorianalyysi yhdisti nestevirtauksen turbiinin muotoon ja pyörimiseen. Aluksi käytettiin graafisia laskentamenetelmiä. Turbiinin osien perusmittoja koskevat kaavat on dokumentoitu hyvin, ja erittäin tehokas kone voidaan suunnitella luotettavasti mihin tahansa nestevirtaustilanteeseen. Osa laskelmista on empiirisiä tai nyrkkisääntöjä, osa perustuu klassiseen mekaniikkaan. Kuten useimmissa teknisissä laskelmissa, yksinkertaistavia oletuksia on tehty.

Turbiiniportaan perustehon laskemiseen voidaan käyttää nopeuskolmioita. Kaasu poistuu paikallaan olevasta turbiinisuuttimen ohjainsiivestä absoluuttisella nopeudella Va1. Roottori pyörii nopeudella U. Suhteessa roottoriin kaasun nopeus sen osuessa roottorin suuaukkoon on Vr1. Roottori kääntää kaasua ja se poistuu roottoriin nähden nopeudella Vr2. Absoluuttisesti tarkasteltuna roottorin ulostulonopeus on kuitenkin Va2. Nopeuskolmiot muodostetaan näiden eri nopeusvektoreiden avulla. Nopeuskolmiot voidaan muodostaa missä tahansa siiven kohdassa (esim. napa, kärki, keskiosa jne.), mutta yleensä ne esitetään keskivaiheen säteen kohdalla. Lavan keskimääräinen suorituskyky voidaan laskea nopeuskolmioista tällä säteellä Eulerin yhtälön avulla:
Δ h = u ⋅ Δ v w {\displaystyle \Delta h=u\cdot \Delta v_w}}

Siten:
Δ h T = u ⋅ Δ v w T {\displaystyle {\frac {\Delta h}{T}}={\frac {u\cdot \Delta v_{w}}{T}}}}

missä:
Δ h {\displaystyle \Delta h}

on ominaisentalpiapudotus vaiheessa T {\displaystyle T}

on turbiinin sisääntulon kokonaislämpötila (tai pysähtymislämpötila) u {\displaystyle u}

on turbiinin roottorin kehänopeus Δ v w {\displaystyle \Delta v_{w}}

on pyörimisnopeuden muutos
Turbiinin painesuhde on funktiona Δ h T {\displaystyle {\frac {\Delta h}{T}}}

ja turbiinin hyötysuhteesta.
Nykyaikainen turbiinisuunnittelu vie laskelmia pidemmälle. Laskennallinen fluididynamiikka luopuu monista yksinkertaistavista oletuksista, joita käytettiin klassisten kaavojen johtamisessa, ja tietokoneohjelmistot helpottavat optimointia. Nämä välineet ovat parantaneet turbiinien suunnittelua tasaisesti viimeisten neljänkymmenen vuoden aikana.
Turbiinin ensisijainen numeerinen luokitus on sen ominaisnopeus. Tämä luku kuvaa turbiinin nopeutta sen maksimihyötysuhteessa tehoon ja virtausmäärään nähden. Ominaisnopeuden on johdettu olevan riippumaton turbiinin koosta. Kun otetaan huomioon nesteen virtausolosuhteet ja haluttu akselin ulostulonopeus, ominaisnopeus voidaan laskea ja valita sopiva turbiinirakenne.
Ominaisnopeuden ja joidenkin perustavanlaatuisten kaavojen avulla voidaan luotettavasti skaalata olemassa oleva, suorituskyvyltään tunnettu turbiinirakenne uuteen kokoon, jolla on vastaava suorituskyky.
Suunnittelun ulkopuolinen suorituskyky esitetään yleensä turbiinikarttana tai -ominaisuutena.
Roottorin lapojen lukumäärä ja staattorin siipien lukumäärä ovat usein kaksi eri alkulukua harmonisten yliaaltojen vähentämiseksi ja lapojen läpimenotaajuuden maksimoimiseksi.