Calcul de ΔS à partir de cycles thermodynamiques
Nous pouvons également calculer un changement d’entropie en utilisant un cycle thermodynamique. Comme vous l’avez appris précédemment, la capacité thermique molaire (Cp) est la quantité de chaleur nécessaire pour élever la température de 1 mol d’une substance de 1°C à pression constante. De même, la Cv est la quantité de chaleur nécessaire pour élever la température d’une mole d’une substance de 1°C à volume constant. L’augmentation de l’entropie avec l’augmentation de la température dans la figure \(\PageIndex{2}\) est approximativement proportionnelle à la capacité thermique de la substance.
Rappelons que la variation d’entropie (ΔS) est liée au flux de chaleur (qrev) par ΔS = qrev/T. Parce que qrev = nCpΔT à pression constante ou nCvΔT à volume constant, où n est le nombre de moles de substance présente, la variation d’entropie pour une substance dont la température passe de T1 à T2 est la suivante :
Comme vous le découvrirez dans des cours de mathématiques plus avancés que ceux requis ici, on peut montrer que cette variation est égale à ce qui suit :Pour une révision des logarithmes naturels, voir la compétence essentielle 6 du chapitre 11 « Liquides ».
\
De même,
\
On peut donc utiliser une combinaison de mesures de capacité thermique (équation 18.20 ou équation 18.21) et de valeurs mesurées expérimentalement des enthalpies de fusion ou de vaporisation si un changement de phase est impliqué (équation 18.18) pour calculer le changement d’entropie correspondant à un changement de température d’un échantillon.
Nous pouvons utiliser un cycle thermodynamique pour calculer le changement d’entropie lorsque le changement de phase d’une substance telle que le soufre ne peut être mesuré directement. Comme indiqué dans l’exercice de l’exemple 6, le soufre élémentaire existe sous deux formes (partie (a) de la figure \(\PageIndex{3}\)) : une forme orthorhombique avec une structure hautement ordonnée (Sα) et une forme monoclinique moins ordonnée (Sβ). La forme orthorhombique (α) est plus stable à température ambiante mais subit une transition de phase vers la forme monoclinique (β) à des températures supérieures à 95,3°C (368,5 K). La transition de Sα à Sβ peut être décrite par le cycle thermodynamique illustré dans la partie (b) de la figure \(\PageIndex{3}\), dans lequel le soufre liquide est un intermédiaire. Le changement d’entropie qui accompagne la conversion du soufre liquide en Sβ (-ΔSfus(β) = ΔS3 dans le cycle) ne peut pas être mesuré directement. Cependant, comme l’entropie est une fonction d’état, ΔS3 peut être calculé à partir de la variation d’entropie globale (ΔSt) pour la transition Sα-Sβ, qui est égale à la somme des valeurs ΔS pour les étapes du cycle thermodynamique, en utilisant l’équation 18.20 et des paramètres thermodynamiques tabulés (les capacités thermiques de Sα et Sβ, ΔHfus(α), et le point de fusion de Sα.)

La résolution de ΔS3 donne une valeur de -3,24 J/(mol-K). Comme prévu pour la conversion d’un état moins ordonné (un liquide) en un état plus ordonné (un cristal), ΔS3 est négatif.
Comment sont mesurées les entropies
L’entropie absolue d’une substance à toute température supérieure à 0 K doit être déterminée en calculant les incréments de chaleur q nécessaires pour amener la substance de 0 K à la température d’intérêt, puis en additionnant les rapports q/T. Deux types de mesures expérimentales sont nécessaires :
- Les enthalpies associées à tout changement de phase que la substance peut subir dans la gamme de température d’intérêt. La fusion d’un solide et la vaporisation d’un liquide correspondent à des augmentations notables du nombre de micro-états disponibles pour accepter l’énergie thermique, donc lorsque ces processus se produisent, l’énergie s’écoulera dans un système, remplissant ces nouveaux micro-états dans la mesure requise pour maintenir une température constante (le point de congélation ou d’ébullition) ; ces entrées d’énergie thermique correspondent aux chaleurs de fusion et de vaporisation. L’augmentation d’entropie associée à la fusion, par exemple, est juste ΔHfusion/Tm.
- La capacité thermique C d’une phase exprime la quantité de chaleur nécessaire pour changer la température d’une petite quantité ΔT , ou plus précisément, d’une quantité infinitésimale dT . Ainsi, l’augmentation d’entropie provoquée par le réchauffement d’une substance sur une plage de températures qui n’englobe pas une transition de phase est donnée par la somme des quantités C dT/T pour chaque incrément de température dT . Ce n’est bien sûr que l’intégrale
\
Parce que la capacité thermique est elle-même légèrement dépendante de la température, les déterminations les plus précises des entropies absolues exigent que la dépendance fonctionnelle de C par rapport à T soit utilisée dans l’intégrale ci-dessus au lieu d’une constante C.
\
Lorsque cela n’est pas connu, on peut prendre une série de mesures de la capacité thermique sur des incréments de température étroits ΔT et mesurer l’aire sous chaque section de la courbe.
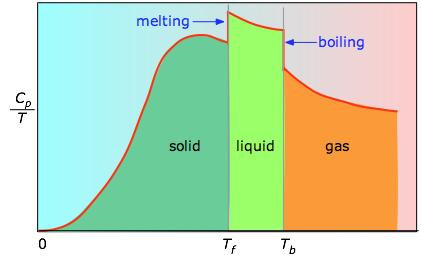
L’aire sous chaque section du tracé représente la variation d’entropie associée au chauffage de la substance sur un intervalle ΔT. Il faut y ajouter les enthalpies de fusion, de vaporisation, et de tout changement de phase solide-solide. Les valeurs de Cp pour les températures proches de zéro ne sont pas mesurées directement, mais peuvent être estimées à partir de la théorie quantique.
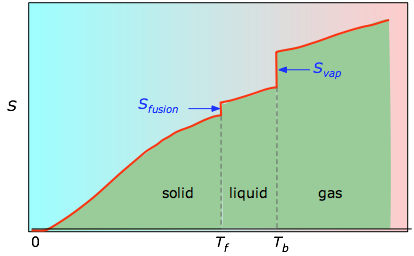
Les aires cumulées de 0 K à toute température donnée (tirées du tracé expérimental de gauche) sont ensuite tracées en fonction de T, et toute entropie de changement de phase telle que Svap = Hvap / Tb est ajoutée pour obtenir l’entropie absolue à la température T.
.