Nombres premiers et nombres composés

Dans le billet d’aujourd’hui, vous apprendrez la différence entre les nombres premiers et les nombres composés. De plus, nous vous montrerons plusieurs exemples pour vous aider à mieux les comprendre.

Que sont les nombres premiers ?

Les nombres premiers sont les nombres qui ne sont divisibles que par eux-mêmes et 1, c’est-à-dire que si on essaie de les diviser par un autre nombre, le résultat n’est pas un nombre entier. Donc, si vous divisez le nombre par autre chose que 1 ou lui-même, vous obtiendrez un reste qui n’est pas zéro.

Nombres premiers jusqu’à 100

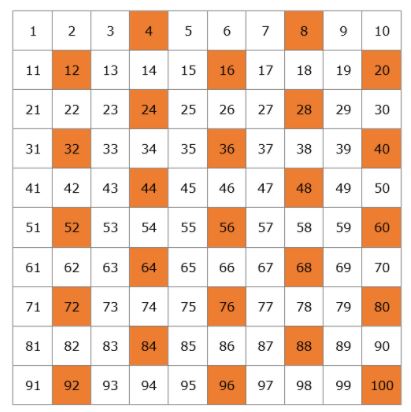
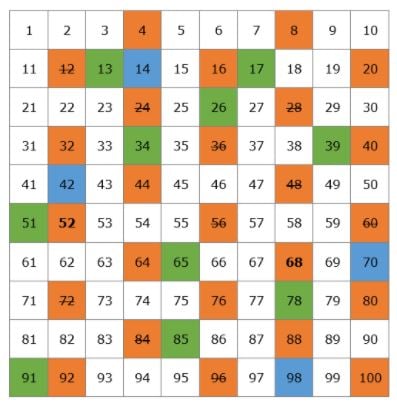
Nous allons créer un tableau avec tous les nombres premiers qui existent jusqu’à 100.

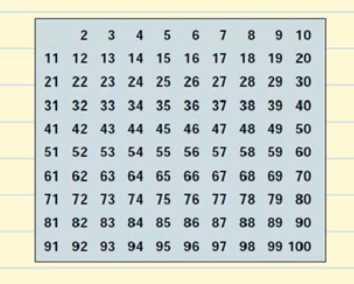
Commençons par 2. 2 est un nombre premier mais tous les multiples de 2 seront des nombres composés puisqu’ils seront divisibles par 2. On raye tous les multiples de 2 sur le tableau.

Le nombre premier suivant est 3, on peut donc rayer tous les multiples de 3 puisqu’ils seront des nombres composés.

Après 3, se trouve le prochain nombre premier 5, donc on raye tous les multiples de 5.

Puis on a le nombre premier 7 et on raye tous les multiples de 7.

Le prochain nombre premier est 11, donc on raye tous les multiples de 11 qui sont 22, 33, 44, 55, 66, 77, 88 et 99. Tous ces nombres avaient déjà été barrés, nous avons donc fini de barrer tous les nombres composés de notre tableau.

C’est notre liste de nombres premiers de 1 à 100. Vous n’avez pas à les mémoriser mais il serait préférable que vous vous souveniez des plus petits nombres, comme 2, 3, 5, 7, 11, 13.

Combien de nombres premiers y a-t-il ?

Le mathématicien grec Eratosthène (3e siècle avant JC) a conçu un moyen rapide de trouver tous les nombres premiers jusqu’à un nombre donné. C’est un procédé appelé le tamis d’Eratosthène.

Notez qu’entre 1 et 100 il y a 25 nombres premiers. Combien de nombres premiers y a-t-il au total ? On sait depuis l’Antiquité qu’il en existe une quantité infinie, il est donc impossible de tous les énumérer. Comme Euclide, qui a été le premier à montrer qu’il y en avait une quantité infinie au 4ème siècle avant JC, ne connaissait pas le concept d’infini, il a dit « les nombres premiers sont plus nombreux que toute multitude fixe d’entre eux », ce qui signifie que si vous imaginez 100, il y en a plus, et si vous imaginez un million, il y en a encore plus.

Nombres premiers de 100 à 1 000

Regardons les nombres premiers de 100 à 1 000.

Nous sommes désolés de ne pas pouvoir tous les montrer, car vous savez qu’il y en a une quantité infinie. 😉

Nombres premiers Exemples

Pour vous aider à mieux comprendre les nombres premiers, nous allons vous expliquer un exercice.

Sara a 6 bonbons qu’elle veut partager, mais elle ne sait pas avec combien de personnes elle peut les partager pour que tout le monde ait la même quantité et qu’il n’en reste aucun. De combien de façons peut-elle le faire ?

Voici Sara et ses 6 bonbons :

Comment peut-on les diviser ?

La première façon, la plus facile, est de les donner à une seule personne, c’est-à-dire de diviser par 1. Ainsi, cette personne aura 6 bonbons.

La prochaine possibilité est de les diviser entre 2 personnes. Comme 6 divisé par 2 fait 3, chaque personne aura 3 bonbons!

Nous allons continuer avec le nombre suivant, 3. Si nous divisons 6 bonbons entre 3 personnes, c’est aussi une division exacte et chaque personne aura 2 bonbons:

Poursuivons avec les nombres. Nous n’avons pas de divisions exactes avec 4 et 5, mais nous en avons avec 6.

Puisque 6 divisé par 6 est 1, nous pouvons donner à 6 enfants 1 bonbon chacun.

Nous allons collecter quelques informations. Nous avons 6 bonbons que nous pouvons partager (avec une division exacte) entre 1, 2, 3 et 6 personnes. En d’autres termes, nous pouvons diviser le nombre 6 et obtenir 0 comme reste lorsque nous le divisons par 1, 2, 3 et 6. Ces nombres sont connus comme les diviseurs de 6.

Nous allons essayer avec un autre nombre, 7 par exemple.

Maintenant, Sara a 7 bonbons et veut les partager, mais elle ne sait pas avec combien de personnes elle peut les partager pour que tout le monde ait la même quantité et qu’il n’en reste aucun. De combien de façons peut-elle le faire ?

Henry a tellement de chance ! Il a obtenu tous les morceaux de bonbons !

Y a-t-il d’autres façons de le faire ? Nous ne pouvons pas diviser 7 par 2, 3, 4, 5 ou 6, …mais 7 est possible !

Sara peut partager les morceaux de bonbons entre 7 personnes, en leur donnant un morceau chacune :

Donc 7 ne peut être divisé que par 1 et 7, ses seuls diviseurs sont 1 et 7. Ce sont les types de nombres que l’on appelle des nombres premiers.

Y a-t-il d’autres nombres premiers ? Bien sûr ! Cherchons-en d’autres:

• C’est 4 ? Non ! Parce que ses diviseurs sont 1, 2 et 4.
• Est-ce 5 ? Oui ! Parce que ses diviseurs sont 1 et 5.
• Est-ce 8 ? Non ! Parce que ses diviseurs sont 1, 2, 4 et 8.

En bref, un nombre est premier s’il n’a que 2 diviseurs : 1 et lui-même.

Maintenant, vous pouvez rechercher beaucoup de nombres premiers !

Comment trouver des nombres premiers

Prêtez bien attention ! Nous allons vous donner une astuce pour savoir si un nombre est premier ou non, sans avoir à chercher ses diviseurs, mais d’une manière plus amusante et qui nous donne les diviseurs (s’ils en ont).

Prenons un nombre au hasard, 16 par exemple.

Pour vérifier si c’est un nombre premier ou non, nous allons utiliser un tableau qui ressemble beaucoup aux cartes Montessori pour multiplier. Et nous allons obtenir autant de boules que le nombre que nous avons choisi. Dans ce cas, 16 boules.

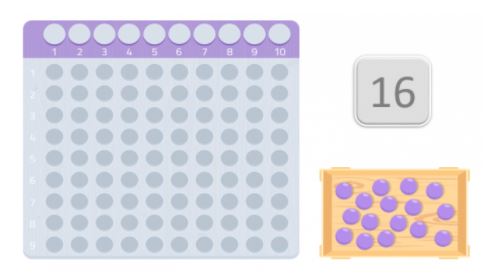
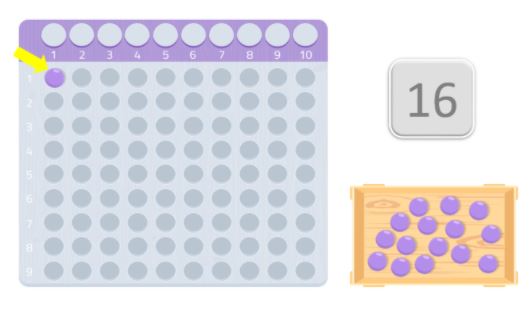
Une fois que nous avons la table et les boules, nous devons les placer sur la table en commençant par le premier espace, en essayant de former un rectangle. Les nombres qui constituent les bords du rectangle sont les diviseurs de ce nombre.

Dans le cas où nous ne parviendrions à former un rectangle qu’avec le même nombre que celui que nous utilisons et le nombre 1, ce sera un nombre premier.

Par exemple, dans ce cas, nous plaçons 8 boules dans la première rangée et 8 autres dans la seconde. Comme vous pouvez le constater, nous avons formé un rectangle et nous pouvons voir que 8, comme 2, sont des diviseurs du nombre 16. Donc, 16 n’est pas un nombre premier car, comme vous le savez, les nombres premiers sont ceux qui ne sont divisibles que par eux-mêmes et 1.

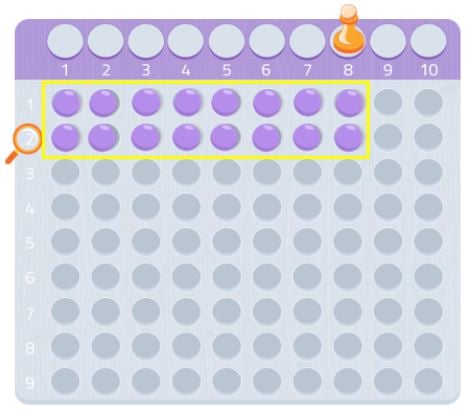
Nous pouvons essayer avec un autre nombre, 7 par exemple.

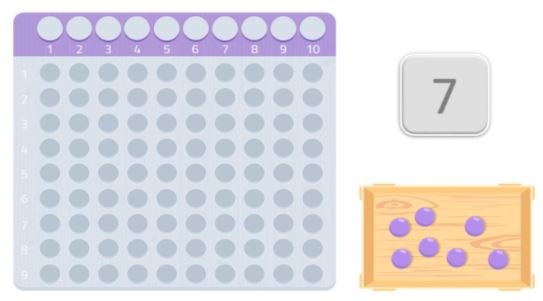
Comme on peut le voir, nous ne pourrions pas faire un rectangle complet, il nous manquerait une boule. Puisque nous sommes incapables de former un rectangle, nous pourrions dire que le nombre 7 n’a pas d’autres diviseurs que lui-même et 1, comme nous pouvons le voir dans l’image suivante.

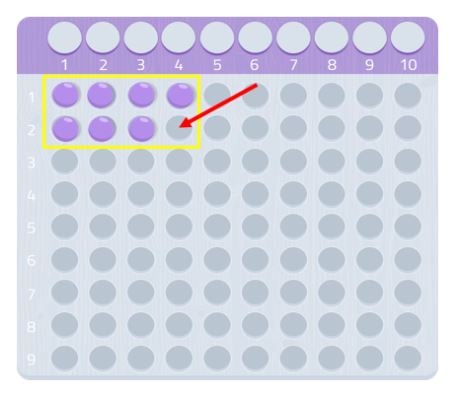
Par conséquent, 7 est un nombre premier !

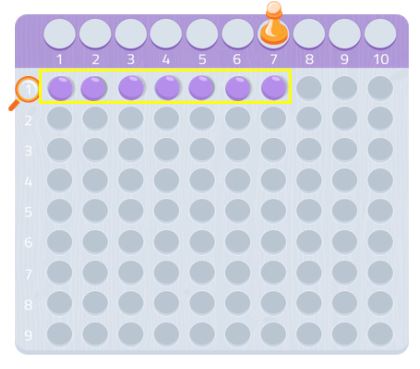
Essayez n’importe quel autre nombre, vous verrez comment cela fonctionne ! Tu peux utiliser du papier millimétré et chercher des rectangles utilisant ce nombre de carrés.

Pourquoi les nombres premiers sont-ils importants ?

Les nombres premiers sont la clé de l’arithmétique, ci-dessous vous verrez un exemple qui démontre leur importance, non seulement en mathématiques mais aussi dans la nature.

Que voulons-nous dire quand nous disons que les nombres premiers sont la clé de l’arithmétique ?

C’est parce que tout nombre consiste en un produit unique constitué d’une série de ces nombres.

On pense qu’ils sont étudiés depuis environ 20 000 ans lorsqu’un de nos ancêtres a inscrit une série de nombres premiers (11, 13, 17 et 19) sur l’os d’Ishango. Comme si c’était une coïncidence, il a été confirmé que les anciens Égyptiens travaillaient avec eux il y a 4 000 ans.

En outre, la nature les connaît très bien et certaines espèces ont pu les découvrir au cours de leur évolution et en tirer profit pour leur survie.

Je fais référence à plusieurs espèces de cigales, comme la Magicicada septendecium qui vit en Amérique du Nord. Cette espèce de cigale a établi son cycle de reproduction autour de 13 ou 17 ans, pas 12, 14, 15, 16 ou 18 – exactement 13 ou 17. Cela leur permet d’éviter les prédateurs qui ont également des cycles de reproduction périodiques ; imaginez un prédateur avec un cycle de reproduction de 4 ans.

Si le cycle de vie d’une cigale était de 12 ou 14 ans, il coïnciderait avec un prédateur très fréquemment, beaucoup plus que s’il était de 13 ou 17 ans. Exactement 2 fois tous les 100 ans, alors qu’autrement, ils coïncideraient sur 11 cycles, ce qui compromettrait le développement de l’espèce.

La sécurité des communications électroniques repose également sur les nombres premiers. Chaque message crypté envoyé sur Internet (réseaux de messages, achats ou banque électronique) est associé à un grand nombre, et il est très difficile de savoir s’il est premier ou non. Le récepteur possède l’un de ses diviseurs, et c’est pourquoi il peut le décrypter. Donc, avoir des nombres premiers est essentiel pour notre vie privée lorsque nous communiquons par voie électronique.

Que sont les nombres composés ?

Les nombres composites sont les nombres qui sont divisibles par 1 et par eux-mêmes ainsi que par d’autres nombres.

Nous allons examiner un exemple de nombre premier et de nombre composite.

11 peut s’écrire comme la multiplication 1 x 11, mais il ne peut pas s’écrire comme toute autre multiplication de nombres naturels. Il n’a que les diviseurs 1 et 11, et c’est donc un nombre premier.

12 peut s’écrire comme la multiplication 1 x 12 et comme la multiplication 3 x 4, et 2 x 6. Comme 12 est divisible par plus de nombres que 1 et lui-même, 12 est un nombre composite.

Est-ce que 1 est un nombre premier ?

Il y a des gens qui le croient parce qu’ils disent que 1 ne peut être divisé que par 1 et lui-même mais en mathématiques, le nombre 1 a été écarté comme nombre premier parce qu’il n’a qu’un seul diviseur. En fait, le critère selon lequel « un nombre entier positif est premier s’il a exactement deux diviseurs positifs » est utilisé pour exclure le nombre 1 de la liste des nombres premiers. Ce n’est pas parce qu’on fait la fine bouche, mais si le nombre un était considéré comme premier, alors de nombreuses propriétés mathématiques devraient être dites différemment.

Donc, 1 est un nombre composite ?

Eh bien, il n’est pas non plus composite puisqu’il ne peut pas être mis comme produit de nombres premiers. Le nombre 1 n’est ni premier ni composite. Et avant que vous ne demandiez, zéro n’est pas premier ou composite non plus mais c’est parce que toutes les considérations que nous expliquions pour les nombres positifs, c’est-à-dire supérieurs à zéro.

Diviseurs d’un nombre

Le diviseur d’un nombre est la valeur qui divise le nombre en parties exactes, c’est-à-dire qui a un reste de 0.

À titre d’exemple, nous allons calculer les diviseurs de 24.

On commence à diviser par les plus petits nombres en commençant par 1.

• 24 / 1 = 24. 1 et 24 sont des diviseurs.
• 24 / 2 = 12. Donc 2 et 12 sont des diviseurs.
• 24 / 3 = 8. Donc 3 et 8 sont des diviseurs.
• 24 / 4 = 6. Donc 4 et 6 sont des diviseurs.
• 24 / 5 = 4. Ce n’est pas une division exacte et il y a un reste de 4, donc 5 n’est pas un diviseur.

Le prochain nombre est 6, mais comme nous savons déjà que 6 est un diviseur de 24, nous avons fini de calculer les diviseurs de 24.

Vidéo : Factorisation et nombres premiers

Si vous souhaitez en savoir plus sur les nombres premiers et les nombres composés, jetez un œil à la vidéo suivante. Vous apprendrez également le concept de factorisation en utilisant la table Montessori.

Cette vidéo est l’un de nos tutoriels interactifs et, bien qu’elle ne soit pas interactive, vous pouvez néanmoins la regarder autant de fois que nécessaire et la partager avec vos amis. Si vous souhaitez accéder à nos tutoriels interactifs, inscrivez-vous sur Smartick ! La méthode en ligne pour aider les enfants de 4 à 14 ans à apprendre et à pratiquer les mathématiques.

Si vous souhaitez continuer à apprendre les nombres premiers et les meilleures mathématiques adaptées à votre niveau, inscrivez-vous sur Smartick et essayez-le gratuitement !

En savoir plus :

• Nombres premiers et nombres composés
• Nombres premiers : Une astuce pour vous aider à les identifier
• Nombres premiers : Comment les trouver avec le tamis d’Eratosthène
• Apprendre à factoriser en nombres premiers
• Activités sur les nombres premiers avec Smartick

.

• Auteur
• Postes récents

Équipe de création de contenu.
Une équipe pluridisciplinaire et multiculturelle composée de mathématiciens, d’enseignants, de professeurs et autres professionnels de l’éducation !
Ils s’efforcent de créer le meilleur contenu mathématique possible.

Derniers messages de Smartick (voir tous)

• Exemples de problèmes de mots mathématiques de 3e année avec solutions – 25/03/2021
• Angles intérieurs consécutifs : Ce qu’ils sont et comment les trouver avec des exemples – 03/11/2021
• Exemples de problèmes de mots de CE1 avec solutions – 02/04/2021

.