On trouve des factorielles partout en combinatoire car c’est là qu’elles sont nées. La factorielle a été créée comme un moyen d’exprimer le nombre d’arrangements d’un groupe d’éléments, que nous trouvons bien sûr en utilisant, dans sa forme la plus basique, la règle de multiplication du comptage.
La factorielle est en quelque sorte l’opération non officielle de la règle de multiplication du comptage.
Pourquoi la factorielle zéro est égale à 1
C’est là que cela devient délicat car si nous ne pensons aux factorielles que dans le contexte dans lequel elles sont habituellement définies, c’est-à-dire.c’est-à-dire le « produit de tous les entiers positifs inférieurs ou égaux au nombre », alors trouver 0 ! est comme se heurter à un mur de briques.
La plupart des gens vous diront que 0 ! est défini comme 1, et si vous demandez pourquoi ils disent simplement « parce que c’est défini comme un ».
Ouais, c’est assez frustrant. C’est l’équivalent mathématique de demander à vos parents pourquoi vous devez suivre une règle arbitraire qu’ils ont inventée et de vous entendre dire « parce que je l’ai dit ».
Bien que cela puisse être une technique parentale acceptée, c’est une façon nulle d’apprendre les mathématiques. Alors, c’est quoi le problème ? Comment avons-nous décidé que la factorielle zéro est égale à un ?
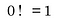
Une compréhension intuitive
Souvenez-vous comment nous avons dit que la factorielle provenait de l’opération mathématique consistant à trouver le nombre de permutations ou d’arrangements d’un ensemble ? (Note : pas les permutations d’un ensemble plus petit à partir d’un ensemble plus grand, mais juste les arrangements d’un ensemble donné.)
La factorielle zéro peut être considérée comme le nombre d’arrangements de zéro élément dans un ensemble, alias l’ensemble vide {}. (Si vous avez déjà étudié les ensembles, peut-être en statistiques de base ou en mathématiques discrètes, vous êtes probablement familier avec le concept d’ensemble vide. C’est littéralement l’ensemble de rien.)
Maintenant si je vous demandais combien d’arrangements il y a d’une chose, vous répondriez 1 parce qu’il n’y a qu’une seule façon d’arranger une chose. La même idée suit ici. Notre « une chose » est l’ensemble vide, et le nombre d’arrangements de l’ensemble vide est un. C’est tout. C’est pourquoi 0 ! égale 1.
Comment simplifier les expressions factorielles
Maintenant que nous avons les bases derrière nous, il est temps pour le cœur de notre tutoriel factoriel : simplifier.
La meilleure façon de voir les mathématiques est en action. Donc, je suis ici pour vous guider à travers les six problèmes montrés dans l’image en haut de ce post ! Nous commencerons gentiment, puis nous passerons à la formule des combinaisons avec des nombres puis des variables, et nous terminerons par des expressions factorielles plus délicates.
❤ STAY CONNECTED ❤
Ne manquez pas un battement, ou un problème de mathématiques !
.