Az SHM egyenletei
Tekintsünk egy súrlódásmentes asztalra rugóhoz rögzített blokkot (\(\(\PageIndex{3}\) ábra). Az egyensúlyi helyzetet (azt a helyzetet, ahol a rugó nincs sem megnyújtva, sem összenyomva) x = 0 -ként jelöljük. Az egyensúlyi helyzetben a nettó erő nulla.
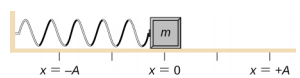
Munkát végzünk a tömbbel, hogy kihúzzuk x = + A helyzetbe, majd kiengedjük a nyugalmi helyzetből. A maximális x-helyzetet (A) a mozgás amplitúdójának nevezzük. A blokk SHM-ben kezd el oszcillálni x = + A és x = -A között, ahol A a mozgás amplitúdója, T pedig a rezgés periódusa. A periódus az egy rezgés időtartamát jelenti. A \(\PageIndex{4}\) ábra a blokk mozgását mutatja, amint a kioldás után másfél oszcillációt végez.
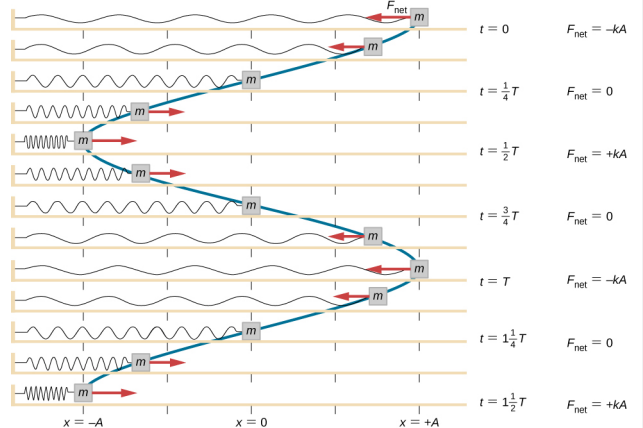
\
A helyzet egyenlete az idő függvényében \(x(t) = A\cos( \omega t)\) jól modellezi az adatokat, ahol a blokk helyzete a t = 0,00 s kezdeti időpontban A amplitúdójú, a kezdeti sebesség pedig nulla. Gyakran előfordul, hogy a kísérleti adatok felvételekor a tömeg helyzete a t = 0,00 s kezdeti időpontban nem egyenlő az amplitúdóval, és a kezdeti sebesség nem nulla. Tekintsük az \(\PageIndex{6}\) ábrán látható 10 másodperces adatokat, amelyeket egy hallgató gyűjtött a laborban.
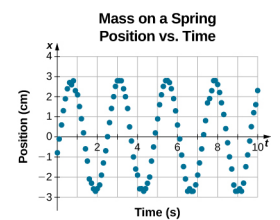
A \(\PageIndex{6}\) ábra adatai még mindig modellezhetők egy periodikus függvénnyel, például egy koszinuszfüggvénnyel, de a függvény jobbra van eltolva. Ezt az eltolódást fáziseltolódásnak nevezik, és általában a görög phi betűvel ábrázolják (\(\phi\)). A rugón lévő blokk helyzetének egyenlete az idő függvényében a következő:
\\
Ez az SHM általános egyenlete, ahol t az idő másodpercben mérve, \(\omega\) a szögfrekvencia inverz másodperces egységekkel, A az amplitúdó méterben vagy centiméterben mérve, és \(\phi\) a fáziseltolódás radiánban mérve (\(\PageIndex{7}\) ábra). Meg kell jegyezni, hogy mivel a szinusz és a koszinusz függvények csak a fáziseltolódásban különböznek, ez a mozgás modellezhető akár a koszinusz, akár a szinusz függvénnyel.
A SHM-ben oszcilláló rugón lévő tömeg sebességét a helyzetegyenlet deriváltjával találhatjuk meg:
\
Mivel a szinuszfüggvény -1 és +1 között oszcillál, a maximális sebesség a szögfrekvencia amplitúdójának szorzata, vmax = A\(\omega\). A maximális sebesség az egyensúlyi helyzetben (x = 0) akkor következik be, amikor a tömeg x = + A felé mozog. A negatív irányú maximális sebesség az egyensúlyi helyzetben (x = 0) akkor következik be, amikor a tömeg x = -A felé mozog, és egyenlő -vmax.
A rugón lévő tömeg gyorsulása a sebesség időbeli deriváltjával állapítható meg:
\
.