Egy szabálytalan sokszög területe

Ez a cikk egy egyszerű megoldást ír le egy geometriai problémára, amelyet az interneten túlságosan bonyolult módon leírtak. A probléma egy kétdimenziós, zárt alakzat, például egy szoba alaprajzának, vagy egy telek, vagy bármilyen más kétdimenziós, határolt alakzat (“szabálytalan sokszög”) területének és kerületének hosszának kiszámítása, függetlenül attól, hogy mennyire bonyolult.

A módszer eredetiségére természetesen nem tartok igényt. Ennek változatai már Gauss óta vagy még korábban is léteztek. De a legtöbb online cikk szükségtelenül bonyolult módon írja le a módszert. A hivatkozások között szerepel a Wikipedia Shoelace Formula szócikke, egy hasonlóan összetett módszer a Polygon szócikkben, és számos olyan szócikk, amelyek úgy tűnik, inkább a szerző erudíciójának demonstrálására vannak kiszámítva, mint a módszer legkevésbé összetett megvalósítására. Ez a cikk (PDF) az egyik legkevésbé bonyolult (de korántsem egyszerű) kifejezést mutatja be:

(1) $A = \frac{1}{2} \left\{ \left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\\ \end{array} \right| + \left|\begin{array}{cc} x_1 & x_2 \\\ y_1 & y_2\\\ \end{array} \right| + \left|\begin{array}{cc} x_2 & x_3 \\\ y_2 & y_3\\\ \end{array} \right| + … + \left|\begin{array}{cc} x_{n-2} & x_{n-1} \\\ y_{n-2} & y_{n-1}\\\ \end{array} \right| + \left|\begin{array}{cc} x_{n-1} & x_0 \\\ y_{n-1} & y_0\\\ \end{array} \right| \right\}$

ahol $x_n,y_n$ egy sokszög csúcsa kartéziánus koordinátákban kifejezve, és $\left|\begin{array}{cc} x_0 & x_1 \\\ y_0 & y_1\\\ \end{array} \right|$ egy determinánsra utal, amelynek értéke $x_0 \times y_1 – y_0 \times x_1$

Ne csüggedjünk a fenti kifejtésen – a módszer használata egyszerűbb, mint a matematikai alapok megértése. Ennek a cikknek a kutatása során tetszőleges számú olyan diákkérdésre adott választ találtam, amelyek annyira bonyolultak voltak, hogy nem tudták volna felvilágosítani a diákot. Ebben a cikkben mindent megteszek azért, hogy ezt a módszert a lehető legegyszerűbbé és legközérthetőbbé tegyem.

A módszer legegyszerűbben algoritmusként fejezhető ki:

• Egy szabálytalan sokszög csúcsai ábrázolhatók kartéziánus koordinátákkal:
• Minden koordinátapár egy területösszegző algoritmusban kerül feldolgozásra, amely így néz ki:
  

  $A = A + \frac{(x_1 \times y_0 – y_1 \times x_0)}{2}$
  $A = A + \frac{(x_2 \times y_1 – y_2 \times x_1)}{2}$
  …

• Egy egyszerű matematikai kifejezés a fentiekre a következő lenne:
  

  (2) Szabálytalan sokszög területe $\displaystyle A = \frac{1}{2} \sum_{i=m}^{n-1}{x_{i+1} \times y_i – y_{i+1} \times x_i}$

• MEGJEGYZÉS: A (2) egyenletben az átvitt ábra az utolsó megadott adatelemmel végződik, nem ismétli meg a kezdeti elemet, mint a fenti (1) egyenletben. Az alább kifejtett céljaim érdekében ez a forma szándékos – egy földmérésnél a terepi adatoknak kell lezárniuk az ábrát, azaz az utolsó elemnek meg kell egyeznie az elsővel. Egy ilyen alkalmazásban az ábra automatikus lezárása az (1) egyenlet szerint olyan hibákat rejtene el, amelyeket ki kell értékelni.

  A felhasználók a földmérési adatok csökkentésétől eltérő célokra a fenti (1) egyenletben látható formát részesíthetik előnyben. Ilyen célokra a feldolgozás során egyszerűen értékeljük újra az első adatelemet a keresztezés végén, vagy adjunk meg olyan adatkészleteket, amelyek az első adatelemet ismétlik meg utolsóként.

• Itt van egy teljes, működő Python függvény:
  

  def find_area(array): a = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) ox,oy = x,y return a/2 

• A fenti “array” argumentum a kartészi $x,y$ koordináták halmaza, i.e. ((10,10),(10,20),(20,20),(20,10),(10,10)). Vegyük észre ezzel az adathalmazzal kapcsolatban, hogy az első adatelem a végén megismétlődik.

• Itt egy kicsit bonyolultabb Python függvény, amely a területet és a kerület hosszát is kiszámítja:
  

  def find_area_perim(array): a = 0 p = 0 ox,oy = array for x,y in array: a += (x*oy-y*ox) p += abs((x-ox)+(y-oy)*1j) ox,oy = x,y return a/2,p 

• Még egyszer ez az emlékeztető: mindkét fenti kódpélda esetében a földmérési adatok redukciójától eltérő alkalmazásokban a megadott adathalmaznak tartalmaznia kell az első adatelem másolatát, mint az utolsó, azaz i.azaz az ábrát kifejezetten le kell zárni.

• A példákhoz azért választottam Pythont, mert egy Python-listázás maximalizálja az algoritmikus értelmet, miközben minimalizálja a cruftot.

• A fenti függvények könnyen, szinte közvetlenül konvertálhatók más nyelvekre – kivéve a fent látható peremösszegzést, amely kihasználja, hogy a Python támogatja a komplex számokat. Az olyan nyelvek esetében, amelyek nem támogatják a komplex számokat, a peremösszegzést így is létrehozhatjuk:

  C/C++: p += sqrt(pow(x-ox,2)+pow(y-oy,2));

  Java: p += Math.sqrt(Math.pow(x-ox,2)+Math.pow(y-oy,2));

• Formálisan a kerület hossza a vektorok nagyságának összege:
  

  (3) A kerület hossza $\displaystyle P = \sum_{i=m}^{n-1}{\sqrt{(x_{i+1}-x_i)^2 + (y_{i+1}- (y_{i+1}-y_i)^2}}}$

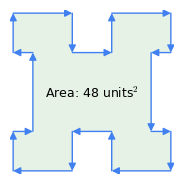
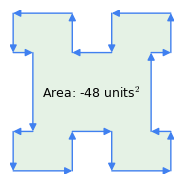1. ábra: Az óramutató járásával megegyezően vs. az óramutató járásával ellentétes irányú vektorok

Itt van néhány fontos tulajdonsága ennek a módszernek:

• A sokszögön belül választott kezdőpontnak nincs jelentősége sem a terület, sem a kerület kiszámítása szempontjából, csak az, hogy az ábra zárt legyen, azaz.azaz az utolsó koordinátának meg kell egyeznie az elsővel.
• “Óramutató járásával megegyező szabály”: a vektorok sorrendjének jelentősége van – ha a kerületet az óramutató járásával megegyező irányban haladjuk át, a terület eredménye pozitív, ha az óramutató járásával ellentétesen, akkor negatív (1. ábra). A módszernek ez a tulajdonsága az, ami az 1. ábrán látható összetett alakzatból kivonja az elhajlások területét – az “elhajlások” az óramutató járásával ellentétes irányú áthaladást jelentenek a sokszögön belül.
• A módszer számos alkalmazása polárvektorokból álló eredeti adatforrásokat használ (példa erre a földmérési jogi leírások), de ehhez a módszerhez kartéziánus koordináták szükségesek. A polárkoordinátákról kartéziánus koordinátákra való átváltás triviális, de fontos szem előtt tartani ezt a követelményt.
• A pontos területszámítás érdekében a leírt sokszögnek zárt alakzatnak kell lennie – az utolsó koordinátának meg kell egyeznie az elsővel. Azoknál az alkalmazásoknál, amelyek olyan terepi adatokat használnak, amelyek hosszvektorokból állnak, amelyeket később kartéziánus formába konvertálnak, érdemes összehasonlítani a kezdő és a befejező kartéziánus koordinátákat – ezeknek egyenlőnek kell lenniük. Például a régebbi földmérések (az olcsó számítógépes teljesítmény korszaka előtt) rendszeresen megbuknak ezen a teszten.

Ez a rész egy teljesen működőképes földrajzi/periméteres számítógép, amely képes feldolgozni a beírt kartézi vagy poláris koordinátaadatpárokat, illetve a földmérési jogi leírásokat. Csak válassza ki az adattípust (kartéziánus x,y koordináták, poláris m,θ koordináták vagy egy felmérési jogi leírás), és adja meg (vagy illessze be) az adatokat az alábbi adatbeviteli területre. Megismerkedés és gyakorlás céljából mintaadatkészleteket is választhat.

A böngésző biztonsági problémái miatt, a túlzott gépelés elkerülése érdekében és jelentős mennyiségű adat más forrásból történő importálásához az olvasóknak a rendszerük vágólapját kell használniuk. Csak másolja az adatokat a forrásalkalmazás vágólapjára, majd kattintson az alábbi adatbeviteli területre, és nyomja meg a Crtl+A billentyűkombinációt az összes kijelöléséhez, a Ctrl+V billentyűkombinációt a máshonnan származó adatok beillesztéséhez, valamint a Ctrl+C billentyűkombinációt a saját beírt adatainak másolásához. A legtöbb böngésző menüpontként is tartalmaz vágólap funkciókat.

Adattípus kiválasztása:

Kartézis (x,y)

polár (m,θ)

Felmérés leírása

Adatbeviteli terület: Válassza ki az összeset: Ctrl+A | Másolás: Ctrl+C | Beillesztés:

Grafikus terület:

Szomorú – az Ön böngészője nem támogatja az ehhez a funkcióhoz szükséges grafikus képességet –
fontolja meg a Google Chrome vagy Firefox telepítését.

Options:

Lines

Arrows

Origin

Center

Length Unit:

Vonalszélesség:

Fordított

Eredmények:Select All: Ctrl+A | Másolás: Ctrl+C | Beillesztés: Ctrl+V

A terület/periméter számítógép háromféle bemeneti móddal rendelkezik:

• Kartézi (x,y) koordinátapárok:

  • Minden koordináta egy kétdimenziós pozíció, amelynek van egy vízszintes (x) és egy függőleges (y) része (kartéziánus koordináta).
  • A koordináták nem kumulatívak – mindegyik önállóan írja le a helyét.
  • Egy négyzet tehát a következő lenne:
    • 0,0 (origó)
    • 0,100 (felfelé)
    • 100,100 (jobbra)
    • 100,0 (lefelé)
    • 0,0 (vissza az origóhoz)
  

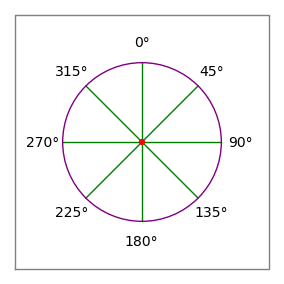  2. ábra: Iránytű rózsa

  • A vesszők a fenti példában csak arra szolgálnak, hogy az olvasó számára csoportosítsák az adatpárokat – a területi számítógép adatelemzője számára nincs jelentőségük.
  • A parser elég robusztus ahhoz, hogy a fenti példát beilleszthessük a számítógép adatbeviteli területére, és működni fog (próbáljuk ki).
  • Az egyetlen korlátozás, hogy a magyarázó megjegyzések nem tartalmazhatnak számokat.

• Poláris (m,θ) koordinátapárok:

  • Minden koordináta egy távolságból és egy fokban megadott szögből (polárvektor) áll.
  • A szögek az iránytű konvenciót követik – 0 fok felfelé vagy “északra”, 90 fok jobbra vagy “keletre” (2. ábra).
  • A korábbi kartéziánus formával ellentétben ezek a koordináták kumulatívak – minden új vektor hozzáadódik a jelenlegi pozícióhoz.
  • Egy négyzet tehát a következő lenne:
    • 100,0 (felfelé)
    • 100,90 (jobbra)
    • 100,180 (lefelé)
    • 100,270 (vissza az origóhoz)
  • Mint korábban, ez a példa is működik, ha beillesztjük a számítógép adatbeviteli területére és a poláris módot választjuk.
  • A polárkoordinátákkal kapcsolatban megjegyezzük, hogy az origó implicit és előre be van állítva x = 0, y = 0.
  

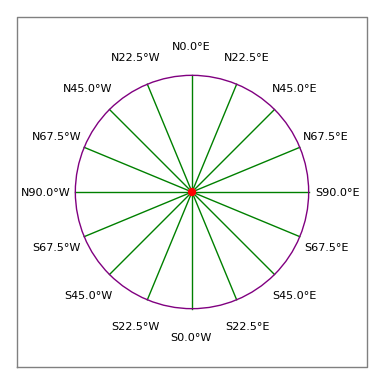  3. ábra: Földmérő iránytű rózsa

• Legális leírás:

  • Először a “Hosszegységek” kiválasztása és az eredmények megjelenítése közötti kapcsolat magyarázata:
    • Minden egyes poligon esetében a területeredmények listája a közös területegységek (láb2, méter2 stb.) rögzített készletének felhasználásával kerül kiszámításra. Ahhoz, hogy ez a területlista értelmes legyen, a bemeneti hosszegységeknek ismerteknek kell lenniük.
    • A kartéziánus és poláris üzemmódban az adatbeviteleknek nincsenek mértékegységei, így a felhasználó választja ki, hogy milyen mértékegységeket rendel a hosszúságokhoz. Így amikor a felhasználó megváltoztatja a hosszegységeket, a területértékek változnak, a hosszcímkék változnak, de a hosszértékek nem.
    • Felmérési módban a jogi leírás tartalmaz hosszegységeket (láb, méter stb.), ami azt jelenti, hogy a hosszegységeket a forrás előre meghatározza. Tehát amikor a felhasználó megváltoztatja a hosszegységeket, az a hosszcímkéket és -értékeket változtatja meg, a területértékeket nem.
  • A felmérési leírás elemzője messze a legkevésbé megbízható a három adatelemzési módszer közül – ez inkább egy kísérlet, mint egy robusztus adatkonverziós módszer.
  • Ezt az elemzőt úgy írtam meg, hogy letöltöttem néhány jogi leírást (amelyek példaként szerepelnek a fenti számológépben), és addig hangoltam az elemző kódját, amíg az összeset sikeresen dekódolni nem sikerült.

  A “siker” kritériumai a következők voltak: az eredménynek ugyanaz a négyzetméteres területe, mint amit a leírás állít, és hogy az ábra “közel legyen”.

  • A “zártság” kifejezést, és különösen a zártság hibáját a felmérési munkában arra használják, hogy leírják, hogy a felmérési traverz végpontja mennyire egyezik meg a kezdőponttal. Ez a valóságban ritkán igaz – a záródási hibák általában a terepi munka hibáiból adódnak, és a régebbi, az olcsó számítógépek megjelenése előtt közzétett felmérések általában meglehetősen rossz záródásúak, valamint a négyzetterület vadul pontatlan becslései.
  • A földmérési jogi leírás egy földterület leírásának formális módja – formája és szintaxisa évtizedek alatt alakult ki a földmérők által kölcsönösen elfogadott, némileg önkényes, közös konvenciók révén.
  • Ez a terület/periméter számítógép esetében a bevitt adatoknak bizonyos szigorú konvenciókat kell követniük, amelyeket néhány, de nem minden jogi leírás betart. Az alapvető elemek a következők:
    • A “kezdőpont” kifejezés megléte, amely elválaszt bizonyos előzetes tartalmat a leírt parcella méreteit leíró tartalomtól. Egyes dokumentumokban a “Valódi kezdőpont”, másokban a “Valódi kezdőpont”, megint másokban a “Kezdőpont” kifejezés szerepel. A sikeres elemzőnek el kell távolítania az e mondat előtti tartalmat, és meg kell tartania az összes utána következő tartalmat.
    • A földmérők által használt polárvektor egy speciális fajtáját leíró mondatok sorozata:
      • Az “Észak” vagy “Dél” szó, vagy annak “N” vagy “S” rövidítése.
      • Ezután egy fokban, percben és másodpercben kifejezett szög.
      • Ezután a “Kelet” vagy “Nyugat” szó, vagy annak “E” vagy “W” rövidítése.
      • Majd egy távolság.
      • Majd egy távolságegység – láb, méter stb.
  • Itt van néhány különböző példa a földmérő vektorokra a jogi leírások mintájából:
    • N 2°0’0″ W – 63.50 feet
    • N90°00’00 “W ALONG A LINE PARALEL WITH SAID NORTH LINE A DISTANCE OF 6.00 FEET
    • North 0°06’O0″ West a distance of 554.86 láb
    • D. 22 fok 41′ 55″ K. 174.10 láb
  • Nézzük meg a fenti példákat, hogy mindegyik különböző szintaxissal rendelkezik. Sok olyan jogi leírás létezik, amelyet ez az elemző nem fog sikeresen dekódolni, csak azért, mert nem próbáltam meg beépíteni a szintaxisukat. De fontos hozzátenni, hogy egy igazán robusztus elemzőnek a létező jogi leírások sokaságához olyan okosnak kellene lennie, mint Watson.
  • A terület/peremterület számítógép felhasználóinak érdemes elkerülniük, hogy egyszerű szöveges jogi leírásokat küldjenek be, és abban reménykedjenek, hogy az elemző majd rájön. A közvetlen kézi bejegyzésekhez (vagy a máshonnan importálható traverzek listájának létrehozásához) ezt a konvenciót használja:
    • Memlékezzen arra, hogy egy elfogadható traverzbejegyzés az “Észak” vagy “Dél” szóból vagy az “N” vagy “S” betűből áll, amelyet legfeljebb három szám követ, amelyek megadják a szög fokát, percét és másodpercét, majd a “Kelet” vagy “Nyugat” szó vagy az “E” vagy “W” betű, majd egy távolság, majd egy távolságegység.
    • Egy elfogadható bejegyzés tehát a következő lenne: “N 30 15 45 W 100 láb”, ami egy 100 láb hosszúságú, északról 30 fok, 15 perc és 45 másodpercnyire nyugatra (azaz nagyjából 330 iránytűfok, lásd a 3. ábrát) mutató keresztezést jelent.
    • A perc és másodperc bejegyzések kihagyhatók, ha nullával egyenlőek, vagy ha a bejegyzés tizedes fokokban vagy fokokban és tizedes percekben van megadva.
  • A nyomtatott jogi leírást nem nehéz ilyen bejegyzésekké alakítani, és a hibák felderítésére számos lehetőség van. Az összes traverz beírása után, ha az ábrán nincs zárási hiba, és ugyanazt a négyzetterületet jelenti, mint az eredeti, akkor jó eséllyel a bejegyzések helyesek (vagy ugyanazokat a hibákat tartalmazzák, mint az eredeti leírás).
  • A jogi leírás ilyen módon történő beírása után, ha elfogadhatatlan zárási hiba van, vagy a négyzetterület rossz, ne feledjük, hogy az eredeti adatok hibásak lehetnek. Bármennyi olyan jogi leírás létezik, amelyet soha nem ellenőriztek egy ilyen számítógépes módszerrel, és amelyek soha nem voltak helyesek.

A kartéziánus (x,y) példákat böngészve figyelje meg a különböző alakzatok terület és kerület arányát. A “furcsa alakú sokszög” aránya köztes, a köré a legkisebb, a Hilbert-téré pedig messze a legnagyobb. Ez az arány magasabb dimenziókba is átnyúlik, ahol köztudottan a gömbnek van a legnagyobb térfogata a felületre vetítve.

A kör példájáról – ez egy “egységkör”, egy olyan kör, amelynek sugara egy. A megadott példa esetében a terület megközelíti a $\pi$ értéket, a kerület pedig a $2\pi$ értéket, ami a megfelelő értékek egy egységkörhöz. Ahhoz, hogy ezek az értékek ne csak közelítések legyenek, hanem pontosan megegyezzenek a $\pi$ és $2\pi$ értékekkel, a sokszög oldalainak számának végtelennek kellene lennie. Ez ellen döntöttem. 🙂

A Hilbert-tér példát egy Sage algoritmussal generáltam, szerény sorrendválasztással (hogy ne generáljak túl sok adatot). Elvileg egy Hilbert-térnek végtelen lehet a kerület és a terület aránya két dimenzióban, vagy a felület és a térfogat aránya három dimenzióban. Hogy lássa, mennyire összetett lehet egy Hilbert-tér, kattintson ide egy 7-es rendű Hilbert-tér megtekintéséhez.

A Hilbert-példával kapcsolatban vegyük észre, hogy a számított terület közel 1/2 egy 1×1-es felület esetén. Ideális esetben, anélkül, hogy szükség lenne egy vonalas ábrát térbeli ábrává alakítani, és a megfelelő algoritmussal a felület területe pontosan 1/2 lenne egy ugyanolyan méretű négyzet területéhez képest.

A poláris beviteli mód nagyjából megegyezik a teknőcgrafikával, ha a “fel” helyett nulla fokot, a “jobbra” helyett 90 fokot stb. használunk, és ha minden egyes forduló- és mozdulatsort egyetlen parancsba tömörítünk. A poláris beviteli mód használata egyszerű módja az összetett alakzatok kézi konstruálásának, mivel a távolságokat és szögeket könnyebb nyomon követni, mint a kartéziánus koordinátákat.

A fent leírt földmérési területszámítási módszert először évekkel ezelőtt használtam, amikor Oregon vidéki részén éltem, olyan emberekkel körülvéve, akiknek tudniuk kellett a birtokaik területét és kerületét. Sok megdöbbentő példával találkoztam, amikor az ingatlanügynökök szemtelenül becsapták az embereket, akiknek nem volt módjuk megtudni, hogy mi folyik itt. Számtalan alkalommal számoltam ki egy területet egy jogi leírásból, hogy aztán kiderüljön, hogy a jótállási okiratban szereplő, területre vonatkozó állítás vadul pontatlan volt – és mindig magasabb, mint a valóság.

Egy alkalommal arra kértek, hogy osszak fel egy ingatlant két egyenlő részre, és készítsek jogi leírást mindkettőhöz. Mivel egy újonnan beszerzett Apple II-vel rendelkeztem (amelynek feldolgozási teljesítménye egy modern ceruzahegyezőé volt), ez nagyon egyszerű volt – de munka közben rájöttem, hogy a teljes terület nagysága körülbelül három hektárral, a teljes terület 25%-ával tévedett. Szembesítettem a tulajdonjoggal foglalkozó céget, amely szemtelenül azt válaszolta: “Látja itt, ahol az okiratban az áll, hogy “többé-kevésbé”?”

Egy másik alkalommal földvásárlásba kezdtem, de a fenti tapasztalatoktól előre figyelmeztetve, amikor megkaptam a tulajdoni lapot, úgy döntöttem, hogy a jogi leírást beírom a programomba, hogy lássam, pontos-e a hektárigénylés. De szörnyülködésemre felfedeztem, hogy az összes tulajdoni lap az adott szakasz parcelláira ugyanazzal a jogi leírással rendelkezett – az elsőként felmért ingatlanéval. Kiderült, hogy a területfejlesztő cég úgy döntött, hogy pénzt takarít meg azzal, hogy az eladásra kínált tucatnyi telek közül csak egyet mért fel, és ezt a jogi leírást szerepelteti az összes tulajdoni lapon. Biztosak voltak benne, hogy ezt megússzák – elvégre ki ért bármit is a matematikához?

Miután vitatkoztam a jogkezelő céggel és a fejlesztővel, és megpróbáltam meggyőzni őket, hogy fizessenek a felmérésekért, hogy a jogi leírások ne legyenek udvarias kitalációk, feladtam, és úgy döntöttem, hogy nem veszem meg a földet. Olyan volt, mint amikor rájöttem, hogyan készül a kolbász – túl sokat lehet tudni.”

• 04.15.2013 Version 1.3. Részletes magyarázatot adtunk az alapértelmezett adatformátumhoz, azaz az első adatpontot utolsóként megismétlő listákhoz.
• 03.24.2013 1.2. verzió. Tovább optimalizálták a felmérés leírásának elemzőjét, több eredményadatmezőt adtak hozzá.
• 03.23.2013 1.1. verzió. Javítottuk a jogi leírás elemzőjét, hogy többféle leírást tudjon kezelni, hozzáadtuk a hosszegységek kiválasztóját és a közös mértékegységekben lévő területek eredménylistáját.
• 03.22.2013 1.0. verzió. Első nyilvános kiadás.