Logisztikus regresszió

A logisztikus regressziót (más néven logit regresszió vagy logit modell) David Cox statisztikus fejlesztette ki 1958-ban, és egy olyan regressziós modell, ahol az Y válaszváltozó kategorikus. A logisztikus regresszió lehetővé teszi egy kategorikus válasz valószínűségének becslését egy vagy több előrejelző változó (X) alapján. Lehetővé teszi, hogy azt mondjuk, hogy egy prediktor jelenléte egy adott kimenetel valószínűségét egy adott százalékkal növeli (vagy csökkenti). Ez a bemutató azt az esetet tárgyalja, amikor az Y bináris, azaz csak két értéket, “0”-t és “1”-t vehet fel, amelyek olyan kimeneteleket képviselnek, mint a megfelelt/nem felelt meg, győzelem/veszteség, életben/halott vagy egészséges/beteg. Azokat az eseteket, amikor a függő változónak kettőnél több kimeneti kategóriája van, multinomiális logisztikus regresszióval lehet elemezni, vagy ha a több kategória rendezett, akkor ordinális logisztikus regresszióval. A diszkriminanciaanalízis azonban a többosztályos osztályozás népszerű módszerévé vált, ezért a következő bemutató anyagunk ezeknek az eseteknek a technikájára fog összpontosítani.

tl;dr
Replikációs követelmények
Miért logisztikus regresszió
Adataink előkészítése
Egyszerű logisztikus regresszió
A koefficiensek értékelése
Jóslatok készítése
Multiple Logistic Regression
Modell kiértékelése & Diagnosztika
Az illeszkedés jósága
Likelihood Ratio Test
Pszeudo
Reziduális értékelés
A jósolt értékek validálása
Klasszifikációs arány
Kiegészítő források

tl;dr

Ez a bemutató anyag bevezetésként szolgál a logisztikus regresszióba, és a következőkre terjed ki1:

Replikációs követelmények: Mire lesz szüksége az ebben az oktatóanyagban szereplő elemzés reprodukálásához
Miért logisztikus regresszió: Miért használjuk a logisztikus regressziót?
Adataink előkészítése: Adataink előkészítése a modellezéshez
Egyszerű logisztikus regresszió: Az Y válasz valószínűségének előrejelzése egyetlen X prediktor változóval
Többszörös logisztikus regresszió: Az Y válasz valószínűségének előrejelzése több prediktor változóval
Modellértékelés & diagnosztika: Mennyire illeszkedik a modell az adatokhoz? Mely prediktorok a legfontosabbak? Pontosak-e az előrejelzések?

Replikációs követelmények

Ez a bemutató elsősorban a ISLR csomag által biztosított Default adatokat használja. Ez egy szimulált adathalmaz, amely tízezer ügyfélre vonatkozó információkat tartalmaz, például azt, hogy az ügyfél nemteljesített-e, diák-e, az ügyfél által hordozott átlagos egyenleg és az ügyfél jövedelme. Használni fogunk még néhány csomagot, amelyek adatmanipulációs, vizualizációs, csővezeték-modellezési funkciókat és a modell kimenetét rendező funkciókat biztosítanak.

# Packageslibrary(tidyverse) # data manipulation and visualizationlibrary(modelr) # provides easy pipeline modeling functionslibrary(broom) # helps to tidy up model outputs# Load data (default <- as_tibble(ISLR::Default))## # A tibble: 10,000 × 4## default student balance income## <fctr> <fctr> <dbl> <dbl>## 1 No No 729.5265 44361.625## 2 No Yes 817.1804 12106.135## 3 No No 1073.5492 31767.139## 4 No No 529.2506 35704.494## 5 No No 785.6559 38463.496## 6 No Yes 919.5885 7491.559## 7 No No 825.5133 24905.227## 8 No Yes 808.6675 17600.451## 9 No No 1161.0579 37468.529## 10 No No 0.0000 29275.268## # ... with 9,990 more rows

Miért logisztikus regresszió

Kvalitatív válasz esetén a lineáris regresszió nem megfelelő. Miért nem? Tegyük fel, hogy a sürgősségi osztályon egy beteg egészségügyi állapotát próbáljuk megjósolni a tünetei alapján. Ebben az egyszerűsített példában három lehetséges diagnózis van: stroke, kábítószer-túladagolás és epilepsziás roham. Megfontolhatjuk ezen értékek kódolását egy mennyiségi válaszváltozóként, Y , a következőképpen:

Ezzel a kódolással a legkisebb négyzetek segítségével egy lineáris regressziós modellt illeszthetünk az Y előrejelzésére egy sor prediktor alapján . Sajnos ez a kódolás sorrendiséget feltételez a kimeneteken, a gyógyszer-túladagolást a stroke és az epilepsziás roham közé helyezi, és ragaszkodik ahhoz, hogy a stroke és a gyógyszer-túladagolás közötti különbség ugyanaz, mint a gyógyszer-túladagolás és az epilepsziás roham közötti különbség. A gyakorlatban nincs különösebb oka annak, hogy ennek így kell lennie. Például választhatnánk egy ugyanilyen ésszerű kódolást,

ami teljesen más kapcsolatot jelentene a három állapot között. Mindegyik ilyen kódolás alapvetően eltérő lineáris modelleket eredményezne, amelyek végső soron a tesztmegfigyelésekre vonatkozó előrejelzések különböző csoportjaihoz vezetnének.

A mi adataink szempontjából relevánsabb, ha egy ügyfelet az egyenlege alapján próbálunk magas vs. alacsony kockázatú nemteljesítőnek minősíteni, akkor lineáris regressziót használhatnánk; az alábbi bal oldali ábra azonban azt mutatja, hogy a lineáris regresszió hogyan jósolná meg a nemteljesítés valószínűségét. Sajnos a nullához közeli egyenlegek esetén negatív nemteljesítési valószínűséget jósolunk; ha nagyon nagy egyenlegekre jósolnánk, akkor 1-nél nagyobb értékeket kapnánk. Ezek az előrejelzések nem ésszerűek, mivel természetesen a nemteljesítés valódi valószínűségének a hitelkártyaegyenlegtől függetlenül 0 és 1 közé kell esnie.

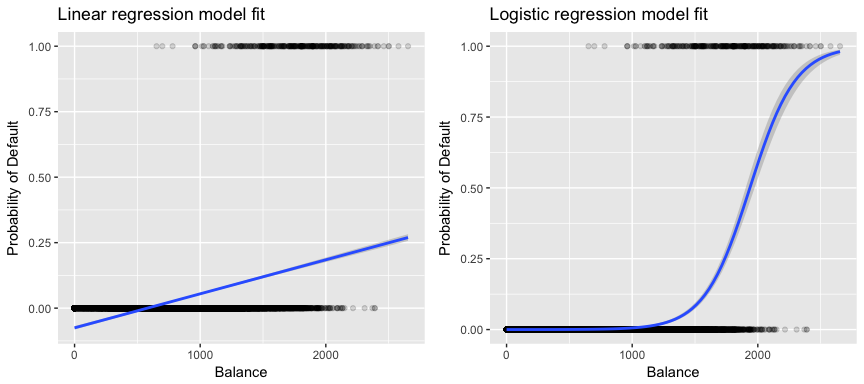
A probléma elkerülése érdekében a p(X)-t olyan függvény segítségével kell modelleznünk, amely X minden értékére 0 és 1 közötti kimenetet ad. Számos függvény megfelel ennek a leírásnak. A logisztikus regresszióban a logisztikus függvényt használjuk, amelyet az 1. egyenlet definiál, és amelyet a fenti jobb oldali ábra szemléltet.

Adataink előkészítése

A regressziós oktatóanyaghoz hasonlóan az adatainkat egy gyakorló (60%) és egy tesztelő (40%) adathalmazra osztjuk, hogy felmérhessük, milyen jól teljesít a modellünk egy mintán kívüli adathalmazon.

set.seed(123)sample <- sample(c(TRUE, FALSE), nrow(default), replace = T, prob = c(0.6,0.4))train <- defaulttest <- default

Egyszerű logisztikus regresszió

Logisztikus regressziós modellt fogunk illeszteni annak érdekében, hogy megjósoljuk egy ügyfél nemteljesítésének valószínűségét az ügyfél által hordozott átlagos egyenleg alapján. A glm függvény általánosított lineáris modelleket illeszt, amely a logisztikus regressziót is magában foglaló modellosztály. A glm függvény szintaxisa hasonló a lm szintaxisához, azzal a különbséggel, hogy át kell adnunk a family = binomial argumentumot, hogy megmondjuk az R-nek, hogy logisztikus regressziót futtasson, és ne valamilyen más típusú általánosított lineáris modellt.

model1 <- glm(default ~ balance, family = "binomial", data = train)

A háttérben a glm, maximális valószínűséget használ a modell illesztéséhez. A maximális valószínűség logisztikus regressziós modell illesztésére való használatának alapvető intuíciója a következő: olyan becsléseket keresünk az és értékekre, hogy a nemfizetés előrejelzett valószínűsége minden egyes egyén esetében az 1. egyenlet segítségével a lehető legjobban megfeleljen az egyén megfigyelt nemfizetési státuszának. Más szóval, megpróbálunk olyan és-t találni, hogy ezeket a becsléseket az 1. egyenletben megadott p(X) modellbe beillesztve egy egyhez közeli számot kapjunk az összes nemteljesítő egyénre, és egy nullához közeli számot az összes nemteljesítő egyénre. Ez az intuíció formalizálható egy matematikai egyenlet segítségével, amelyet valószínűségi függvénynek nevezünk:

A becsléseket és úgy választjuk meg, hogy maximalizáljuk ezt a valószínűségi függvényt. A maximális valószínűség egy nagyon általános megközelítés, amelyet számos olyan nemlineáris modell illesztésére használnak, amelyeket a későbbi oktatóanyagokban fogunk megvizsgálni. Az eredmény egy S alakú valószínűségi görbe, amelyet az alábbiakban szemléltetünk (megjegyezzük, hogy a logisztikus regresszió illeszkedési vonalának ábrázolásához a válaszváltozónkat bináris kódú változóvá kell alakítanunk).

default %>% mutate(prob = ifelse(default == "Yes", 1, 0)) %>% ggplot(aes(balance, prob)) + geom_point(alpha = .15) + geom_smooth(method = "glm", method.args = list(family = "binomial")) + ggtitle("Logistic regression model fit") + xlab("Balance") + ylab("Probability of Default")

A lineáris regresszióhoz hasonlóan a summary vagy glance segítségével értékelhetjük a modellt. Vegyük észre, hogy az együttható kimeneti formátuma hasonló a lineáris regresszióban látottakhoz; a summary alján található illeszkedés jóságának részletei azonban eltérnek. Erre később bővebben kitérünk, de csak annyit jegyezzünk meg, hogy a deviancia szót látja. Az eltérés analóg a lineáris regresszióban szereplő négyzetek összegének számításával, és a logisztikus regressziós modellben az adatokhoz való illeszkedés hiányának mérőszáma. A nulla deviancia a különbséget jelenti egy olyan modell között, amely csak a metszetet tartalmazza (ami azt jelenti, hogy “nincsenek prediktorai”) és egy telített modell (egy elméletileg tökéletes illeszkedésű modell) között. A cél az, hogy a modell eltérése (amelyet reziduális eltérésként jelölünk) alacsonyabb legyen; a kisebb értékek jobb illeszkedést jeleznek. Ebből a szempontból a nullmodell egy olyan kiindulási alapot biztosít, amely alapján a prediktormodelleket összehasonlíthatjuk.

summary(model1)## ## Call:## glm(formula = default ~ balance, family = "binomial", data = train)## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -2.2905 -0.1395 -0.0528 -0.0189 3.3346 ## ## Coefficients:## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.101e+01 4.887e-01 -22.52 <2e-16 ***## balance 5.669e-03 2.949e-04 19.22 <2e-16 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## ## (Dispersion parameter for binomial family taken to be 1)## ## Null deviance: 1723.03 on 6046 degrees of freedom## Residual deviance: 908.69 on 6045 degrees of freedom## AIC: 912.69## ## Number of Fisher Scoring iterations: 8

A koefficiensek értékelése

Az alábbi táblázat azokat a koefficiensbecsléseket és kapcsolódó információkat mutatja, amelyek egy logisztikus regressziós modell illesztéséből származnak a default = igen valószínűségének előrejelzése érdekében az egyenleg felhasználásával. Ne feledje, hogy a logisztikus regresszióból származó együtthatóbecslések a prediktor és a válaszváltozó közötti kapcsolatot logaritmikus esélyskálán jellemzik (további részletekért lásd az ISLR1 3. fejezetét). Így azt látjuk, hogy ; ez azt jelzi, hogy az egyenleg növekedése a nemfizetés valószínűségének növekedésével jár. Pontosabban, az egyenleg egy egységnyi növekedése a nemfizetés logaritmikus esélyének 0,0057 egységgel való növekedésével jár.

tidy(model1)## term estimate std.error statistic p.value## 1 (Intercept) -11.006277528 0.488739437 -22.51972 2.660162e-112## 2 balance 0.005668817 0.000294946 19.21985 2.525157e-82

Az egyenleg együtthatót tovább értelmezhetjük a következőképpen – a havi egyenleg minden egyes dollárnyi növekedése esetén az ügyfél nemfizetésének esélye 1-szeresére nő.0057.

exp(coef(model1))## (Intercept) balance ## 1.659718e-05 1.005685e+00

A koefficiens kimenetének számos szempontja hasonló a lineáris regresszió kimeneténél tárgyaltakhoz. Például az együtthatóbecslések konfidenciaintervallumait és pontosságát a standard hibáik kiszámításával mérhetjük. Például < 2e-16 p-értékkel rendelkezik, ami arra utal, hogy statisztikailag szignifikáns kapcsolat van a hordozott egyenleg és a nemfizetés valószínűsége között. A standard hibák segítségével konfidenciaintervallumokat is kaphatunk, ahogyan azt a lineáris regresszió bemutatójában tettük:

confint(model1)## 2.5 % 97.5 %## (Intercept) -12.007610373 -10.089360652## balance 0.005111835 0.006269411

Jóslatok készítése

Amikor az együtthatókat már megbecsültük, egyszerű feladat kiszámítani a nemfizetés valószínűségét bármely adott hitelkártyaegyenlegre. Matematikailag a modellünkből származó együtthatóbecslések felhasználásával azt jósoljuk, hogy egy 1000 dolláros egyenleggel rendelkező egyén nemteljesítési valószínűsége kevesebb, mint 0,5%

A nemteljesítés valószínűségét az R-ben a predict függvény segítségével tudjuk megjósolni (ügyeljünk arra, hogy a type = "response" szerepeljen benne). Itt összehasonlítjuk a nemfizetés valószínűségét az 1000 és 2000 dolláros egyenlegek alapján. Mint látható, ahogy az egyenleg 1000 dollárról 2000 dollárra nő, a nemfizetés valószínűsége jelentősen, 0,5%-ról 58%-ra nő!

predict(model1, data.frame(balance = c(1000, 2000)), type = "response")## 1 2 ## 0.004785057 0.582089269

A logisztikus regressziós modellel minőségi prediktorokat is használhatunk. Példaként illeszthetünk egy olyan modellt, amely a student változót használja.

model2 <- glm(default ~ student, family = "binomial", data = train)tidy(model2)## term estimate std.error statistic p.value## 1 (Intercept) -3.5534091 0.09336545 -38.05914 0.000000000## 2 studentYes 0.4413379 0.14927208 2.95660 0.003110511

A student = Yes változóhoz tartozó együttható pozitív, és a hozzá tartozó p-érték statisztikailag szignifikáns. Ez azt jelzi, hogy a hallgatóknak általában magasabb a nemteljesítési valószínűsége, mint a nem hallgatóknak. Valójában ez a modell azt sugallja, hogy egy diáknak közel kétszer akkora esélye van a nemteljesítésre, mint a nem diákoknak. A következő szakaszban azonban látni fogjuk, hogy miért.

predict(model2, data.frame(student = factor(c("Yes", "No"))), type = "response")## 1 2 ## 0.04261206 0.02783019

Multiple Logistic Regression

A modellünket az egyenletben látható módon ki is bővíthetjük. 1 úgy, hogy egy bináris választ több prediktor segítségével jósolhatunk meg, ahol a p prediktorok:

Menjünk tovább, és illesszünk be egy olyan modellt, amely az egyenleg, a jövedelem (ezer dollárban) és a hallgatói státusz változók alapján jósolja meg a nemfizetés valószínűségét. Itt egy meglepő eredményt kapunk. Az egyenleghez és a hallgatói=Igen státuszhoz kapcsolódó p-értékek nagyon kicsik, ami azt jelzi, hogy e változók mindegyike összefügg a nemfizetés valószínűségével. A hallgató változó együtthatója azonban negatív, ami azt jelzi, hogy a hallgatók kisebb valószínűséggel válnak fizetésképtelenné, mint a nem hallgatók. Ezzel szemben a hallgatói változó együtthatója a 2. modellben, ahol csak a hallgatói státusz alapján jósoltuk meg a nemfizetés valószínűségét, azt jelezte, hogy a hallgatóknak nagyobb a nemfizetés valószínűsége. Mi az oka?

model3 <- glm(default ~ balance + income + student, family = "binomial", data = train)tidy(model3)## term estimate std.error statistic p.value## 1 (Intercept) -1.090704e+01 6.480739e-01 -16.8299277 1.472817e-63## 2 balance 5.907134e-03 3.102425e-04 19.0403764 7.895817e-81## 3 income -5.012701e-06 1.078617e-05 -0.4647343 6.421217e-01## 4 studentYes -8.094789e-01 3.133150e-01 -2.5835947 9.777661e-03

Az alábbi ábra jobb oldali panelje magyarázatot ad erre az ellentmondásra. A hallgató és az egyenleg változók korrelálnak egymással. A diákok általában magasabb adóssággal rendelkeznek, ami viszont a nemfizetés nagyobb valószínűségével jár együtt. Más szóval, a diákok nagyobb valószínűséggel rendelkeznek nagy hitelkártyaegyenleggel, ami – amint azt az alábbi ábra bal oldali paneljéből tudjuk – általában magas nemteljesítési rátával jár együtt. Így annak ellenére, hogy egy adott hitelkártyaegyenleggel rendelkező egyéni diák esetében kisebb a nemfizetés valószínűsége, mint egy ugyanilyen hitelkártyaegyenleggel rendelkező nem diák esetében, az a tény, hogy a diákok összességében magasabb hitelkártyaegyenleggel rendelkeznek, azt jelenti, hogy a diákok összességében magasabb arányban nemfizetnek, mint a nem diákok. Ez fontos különbségtétel egy hitelkártya-társaság számára, amely megpróbálja meghatározni, hogy kinek ajánljon hitelt. Egy diák kockázatosabb, mint egy nem diák, ha nem áll rendelkezésre információ a diák hitelkártyaegyenlegéről. Ez a diák azonban kevésbé kockázatos, mint egy nem diák ugyanolyan hitelkártyaegyenleggel!

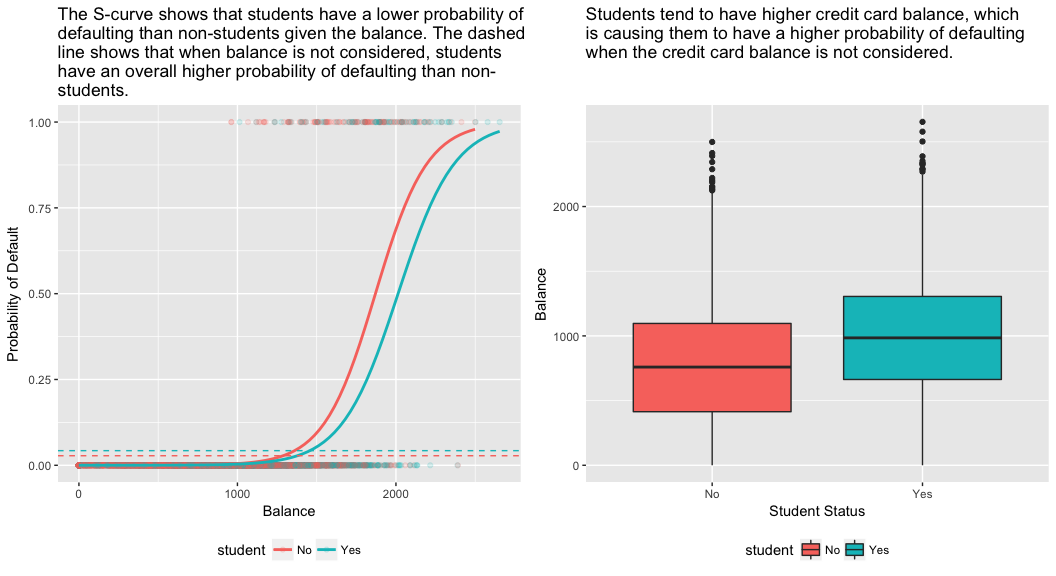
Ez az egyszerű példa jól szemlélteti a csak egyetlen prediktort tartalmazó regressziók elvégzésével kapcsolatos veszélyeket és finomságokat, amikor más prediktorok is relevánsak lehetnek. Az egy prediktor alkalmazásával kapott eredmények egészen mások lehetnek, mint a több prediktor alkalmazásával kapott eredmények, különösen akkor, ha a prediktorok között korreláció van. Ezt a jelenséget confoundingnak nevezzük.

Más prediktorváltozók esetén néha szeretnénk megérteni, hogy melyik változó van a legnagyobb hatással a válaszváltozó (Y) változó előrejelzésére. Ezt a caret csomagból származó varImp segítségével tehetjük meg. Itt azt látjuk, hogy a mérleg nagy különbséggel a legfontosabb, míg a hallgatói státusz kevésbé fontos, amit a jövedelem követ (amely egyébként is jelentéktelennek bizonyult (p = .64)).

caret::varImp(model3)## Overall## balance 19.0403764## income 0.4647343## studentYes 2.5835947

Amint korábban, ezzel a modellel is könnyen tudunk előrejelzéseket készíteni. Például egy 1500 dolláros hitelkártyaegyenleggel és 40 000 dolláros jövedelemmel rendelkező diák esetében a nemfizetés becsült valószínűsége

Egy nem diák esetében ugyanezzel az egyenleggel és jövedelemmel a nemfizetés becsült valószínűsége

new.df <- tibble(balance = 1500, income = 40, student = c("Yes", "No"))predict(model3, new.df, type = "response")## 1 2 ## 0.05437124 0.11440288

Azt látjuk tehát, hogy adott egyenleg és jövedelem esetén (bár a jövedelem nem szignifikáns) egy diáknak körülbelül fele akkora a nemfizetés valószínűsége, mint egy nem diáknak.

Modell kiértékelése & Diagnosztika

Ezidáig három logisztikus regressziós modellt építettünk, és megvizsgáltuk az együtthatókat. Néhány kritikus kérdés azonban továbbra is fennáll. Jók-e a modellek? Mennyire illeszkedik a modell az adatokhoz? És mennyire pontosak az előrejelzések egy mintán kívüli adatsoron?

Az illeszkedés jósága

A lineáris regresszió bemutatójában láttuk, hogy az F-statisztika, valamint a kiigazított , és a reziduális diagnosztika hogyan tájékoztat minket arról, hogy a modell mennyire jól illeszkedik az adatokhoz. Itt megnézünk néhány módszert arra, hogyan értékelhetjük a logit-modelleink illeszkedésének jóságát.

Likelihood Ratio Test

Először is, a Likelihood Ratio Test segítségével értékelhetjük, hogy a modelljeink javítják-e az illeszkedést. A prediktorváltozók hozzáadása egy modellhez szinte mindig javítja a modell illeszkedését (azaz növeli a log likelihoodot és csökkenti a modell eltérését a null-eltéréshez képest), de tesztelni kell, hogy a modell illeszkedésében megfigyelt különbség statisztikailag szignifikáns-e. A modell illeszkedésében megfigyelt különbség statisztikailag szignifikáns. Ezt a tesztet a anova segítségével végezhetjük el. Az eredmények azt mutatják, hogy az model1-hoz képest az model3 több mint 13-mal csökkenti a reziduális devianciát (ne feledjük, a logisztikus regresszió egyik célja, hogy olyan modellt találjon, amely minimalizálja a deviancia reziduálisát). Ami még fontosabb, hogy ez a javulás statisztikailag szignifikáns, p = 0,001. Ez arra utal, hogy a model3 valóban jobb modellillesztést biztosít.

anova(model1, model3, test = "Chisq")## Analysis of Deviance Table## ## Model 1: default ~ balance## Model 2: default ~ balance + income + student## Resid. Df Resid. Dev Df Deviance Pr(>Chi) ## 1 6045 908.69 ## 2 6043 895.02 2 13.668 0.001076 **## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pszeudo

A közönséges legkisebb négyzetek becslésével végzett lineáris regressziótól eltérően nincs olyan statisztika, amely megmagyarázná, hogy a függő változó varianciájának mekkora hányadát magyarázzák a prediktorok. Van azonban számos olyan pszeudo mérőszám, amely értékes lehet. A legjelentősebb a McFadden-féle , amely a következőképpen van definiálva:

ahol a log likelihood értéke az illesztett modellhez és a log likelihood értéke a nullmodellhez, ahol csak egy metszéspont van prediktorként. A mérőszám 0 és valamivel 1 alatt van, a nullához közelebbi értékek azt jelzik, hogy a modellnek nincs előrejelző ereje. A lineáris regressziótól eltérően azonban a modellek ritkán érnek el magas McFadden-értéket. Valójában McFadden saját szavaival élve a McFadden pszeudo értékkel rendelkező modellek nagyon jó illeszkedést jelentenek. A McFadden pszeudo-értékeket a modelljeinkre vonatkozóan a következőkkel tudjuk értékelni:

list(model1 = pscl::pR2(model1), model2 = pscl::pR2(model2), model3 = pscl::pR2(model3))## $model1## McFadden ## 0.4726215 ## ## $model2## McFadden ## 0.004898314 ## ## $model3## McFadden ## 0.4805543

Láthatjuk, hogy a 2. modellnek nagyon alacsony értéke van, ami alátámasztja a rossz illeszkedést. Az 1. és 3. modell értékei azonban sokkal magasabbak, ami arra utal, hogy az alapértelmezett adatok varianciájának megfelelő részét magyarázzák. Továbbá azt látjuk, hogy a 3. modell csak nagyon kis mértékben javítja az értéket.

Reziduális értékelés

Ne feledjük, hogy a logisztikus regresszió nem feltételezi, hogy a reziduumok normális eloszlásúak, sem azt, hogy a variancia állandó. A deviancia reziduum azonban hasznos annak megállapítására, ha az egyes pontokat nem illeszti jól a modell. Itt a standardizált deviancia-maradványokat illeszthetjük, hogy megnézzük, hányan haladják meg a 3 standard eltérést. Először a augment segítségével kivonunk néhány hasznos darabot a modelleredményekből, majd folytatjuk az ábrázolást.

model1_data <- augment(model1) %>% mutate(index = 1:n())ggplot(model1_data, aes(index, .std.resid, color = default)) + geom_point(alpha = .5) + geom_ref_line(h = 3)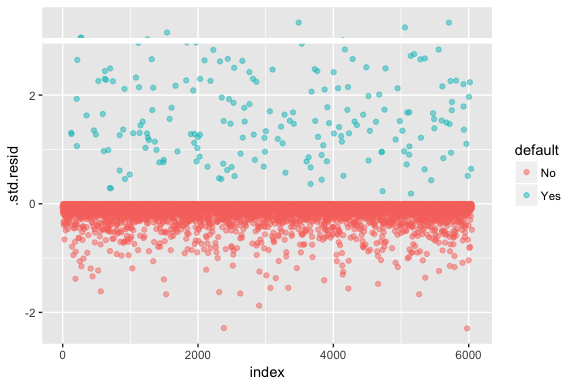

Azok a standardizált maradékok, amelyek meghaladják a 3-at, lehetséges kiugró értékeket jelentenek, és nagyobb figyelmet érdemelnek. Ezekre a reziduumokra szűrhetünk, hogy közelebbről megvizsgálhassuk őket. Láthatjuk, hogy ezek a megfigyelések mind olyan ügyfeleket képviselnek, akik a normál nemfizetőknél jóval alacsonyabb költségvetéssel nem teljesítettek.

model1_data %>% filter(abs(.std.resid) > 3)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 Yes 1118.7010 -4.664566 0.1752745 3.057432 0.0002841609 0.3857438 0.01508609 3.057867 271## 2 Yes 1119.0972 -4.662320 0.1751742 3.056704 0.0002844621 0.3857448 0.01506820 3.057139 272## 3 Yes 1135.0473 -4.571902 0.1711544 3.027272 0.0002967274 0.3857832 0.01435943 3.027721 1253## 4 Yes 1066.8841 -4.958307 0.1885550 3.151288 0.0002463229 0.3856189 0.01754100 3.151676 1542## 5 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 6 Yes 1143.6805 -4.522962 0.1689933 3.011233 0.0003034789 0.3858039 0.01398491 3.011690 4142## 7 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 8 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709

A lineáris regresszióhoz hasonlóan a befolyásoló megfigyeléseket is azonosíthatjuk a Cook-féle távolságértékekkel. Itt az 5 legnagyobb értéket azonosítjuk.

plot(model1, which = 4, id.n = 5)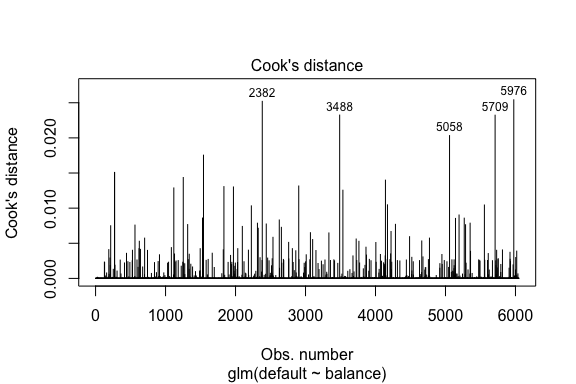

És ezeket is tovább vizsgálhatjuk. Itt láthatjuk, hogy a legnagyobb öt befolyásoló pont közé tartoznak:

azok az ügyfelek, akik nagyon alacsony egyenleggel nem teljesítettek, és
két olyan ügyfél, akik nem teljesítettek, mégis 2000 dollár feletti egyenleggel rendelkeztek

Ez azt jelenti, hogy ha ezeket a megfigyeléseket eltávolítanánk (nem ajánlott), a logisztikus regressziós S-görbénk alakja, helye és konfidenciaintervalluma valószínűleg eltolódna.

model1_data %>% top_n(5, .cooksd)## default balance .fitted .se.fit .resid .hat .sigma .cooksd .std.resid index## 1 No 2388.1740 2.531843 0.2413764 -2.284011 0.0039757771 0.3866249 0.02520100 -2.288565 2382## 2 Yes 961.4889 -5.555773 0.2163846 3.334556 0.0001796165 0.3853639 0.02324417 3.334855 3488## 3 Yes 1013.2169 -5.262537 0.2026075 3.245830 0.0002105772 0.3854892 0.02032614 3.246172 5058## 4 Yes 961.7327 -5.554391 0.2163192 3.334143 0.0001797543 0.3853645 0.02322988 3.334443 5709## 5 No 2391.0077 2.547907 0.2421522 -2.290521 0.0039468742 0.3866185 0.02542145 -2.295054 5976

A jósolt értékek validálása

Klasszifikációs arány

A jóslási modellek fejlesztése során a legkritikusabb mérőszám arra vonatkozóan, hogy a modell mennyire jól teljesít a célváltozó előrejelzésében a mintán kívüli megfigyeléseken. Először is, a becsült modelleket arra kell használnunk, hogy megjósoljuk az értékeket a képzési adathalmazunkon (train). A predict használatakor ügyeljünk arra, hogy a type = response szerepeljen benne, hogy az előrejelzés visszaadja az alapértelmezés valószínűségét.

test.predicted.m1 <- predict(model1, newdata = test, type = "response")test.predicted.m2 <- predict(model2, newdata = test, type = "response")test.predicted.m3 <- predict(model3, newdata = test, type = "response")

Most összehasonlíthatjuk a megjósolt célváltozót a megfigyelt értékekkel az egyes modellek esetében, és megnézhetjük, melyik teljesít a legjobban. Kezdhetjük a konfúziós mátrix segítségével, amely egy olyan táblázat, amely leírja az egyes modellek osztályozási teljesítményét a tesztadatokon. A táblázat minden egyes kvadránsának fontos jelentése van. Ebben az esetben a sorokban szereplő “Nem” és “Igen” azt jelenti, hogy az ügyfelek nem teljesítettek-e fizetési kötelezettséget vagy sem. Az oszlopokban lévő “HAMIS” és “IGAZ” azt jelenti, hogy megjósoltuk-e az ügyfelek nemteljesítését vagy sem.

igaz pozitívak (jobb alsó kvadráns): Ezek azok az esetek, amikor megjósoltuk, hogy az ügyfél nemteljesít, és valóban így is lett.
igaz negatívak (bal felső kvadráns): Nem jósoltunk nemteljesítést, és az ügyfél nem teljesített.
hamis pozitív esetek (jobb felső kvadráns): Igent jósoltunk, de az ügyfél valójában nem esett késedelembe. (Más néven “I. típusú hiba”.)
hamis negatív (bal alsó): Nemet jósoltunk, de valóban nem teljesítettek. (Más néven “II. típusú hiba”)

Az eredmények azt mutatják, hogy model1 és model3 nagyon hasonlóak. A megjósolt megfigyelések 96%-a valódi negatív, és körülbelül 1%-a valódi pozitív. Mindkét modell II. típusú hibája kevesebb, mint 3%, amikor a modell azt jósolja, hogy az ügyfél nem fog nemteljesíteni, de valójában mégis megtette. És mindkét modell I. típusú hibája kevesebb, mint 1%, amikor a modell azt jósolja, hogy az ügyfél nem fog fizetni, de mégsem tette. model2 Az eredmények jelentősen eltérnek; ez a modell pontosan megjósolja a nem fizetésképtelen ügyfeleket (ami abból adódik, hogy az adatok 97%-a nem fizetésképtelen), de valójában soha nem jósolja meg azokat az ügyfeleket, akik nem fizetnek!”

list( model1 = table(test$default, test.predicted.m1 > 0.5) %>% prop.table() %>% round(3), model2 = table(test$default, test.predicted.m2 > 0.5) %>% prop.table() %>% round(3), model3 = table(test$default, test.predicted.m3 > 0.5) %>% prop.table() %>% round(3))## $model1## ## FALSE TRUE## No 0.962 0.003## Yes 0.025 0.010## ## $model2## ## FALSE## No 0.965## Yes 0.035## ## $model3## ## FALSE TRUE## No 0.963 0.003## Yes 0.026 0.009

A hibás besorolási (más néven hiba) arányokat is szeretnénk megérteni (vagy megfordíthatjuk ezt a pontossági arányokra). Nem látunk nagy javulást az 1. és a 3. modell között, és bár a 2. modellnek alacsony a hibaaránya, ne felejtsük el, hogy soha nem jósolja meg pontosan a ténylegesen nem teljesítő ügyfeleket.

test %>% mutate(m1.pred = ifelse(test.predicted.m1 > 0.5, "Yes", "No"), m2.pred = ifelse(test.predicted.m2 > 0.5, "Yes", "No"), m3.pred = ifelse(test.predicted.m3 > 0.5, "Yes", "No")) %>% summarise(m1.error = mean(default != m1.pred), m2.error = mean(default != m2.pred), m3.error = mean(default != m3.pred))## # A tibble: 1 × 3## m1.error m2.error m3.error## <dbl> <dbl> <dbl>## 1 0.02782697 0.03491019 0.02807994

A zavarmátrixunk nyers értékeit (nem százalékos értékeket) vizsgálva további betekintést nyerhetünk. Nézzük meg az 1. modellt a szemléltetés érdekében. Láthatjuk, hogy összesen van olyan ügyfél, aki nem teljesített. Az összes nemteljesítő ügyfél közül nem volt előre jelzett. Alternatívaként azt is mondhatjuk, hogy csak a nemteljesítés előfordulását jósolták meg – ezt nevezzük a modellünk pontosságának (más néven érzékenységének). Tehát miközben a teljes hibaarány alacsony, a pontossági arány is alacsony, ami nem jó!

table(test$default, test.predicted.m1 > 0.5)## ## FALSE TRUE## No 3803 12## Yes 98 40

Az osztályozási modellek esetében a modell teljesítményének jellemzésekor az érzékenység és a specifikusság kifejezéseket is itt használjuk. Mint már említettük, az érzékenység a pontosság szinonimája. A specificitás azonban a helyesen azonosított, nem hibázók százalékos aránya, itt (a pontosságot itt nagyrészt az határozza meg, hogy adatainkban a megfigyelések 97%-a nem hibázó). Az érzékenység és a specificitás közötti jelentőség a kontextustól függ. Ebben az esetben egy hitelkártya-társaságot valószínűleg jobban érdekli az érzékenység, mivel csökkenteni akarja a kockázatát. Ezért lehet, hogy jobban érdekli őket a modell hangolása, hogy az érzékenységük/pontosságuk javuljon.

A fogadó működési karakterisztika (ROC) az osztályozó teljesítményének vizuális mérőszáma. A helyesen pozitívnak ítélt pozitív adatpontok arányát és a tévesen pozitívnak ítélt negatív adatpontok arányát felhasználva egy olyan grafikont hozunk létre, amely megmutatja a valamit helyesen megjósolni képes arány és a valamit tévesen megjósolni képes arány közötti kompromisszumot. Végső soron a ROC-görbe alatti terület, vagyis az AUC érdekel bennünket. Ez a mérőszám 0,50 és 1,00 között mozog, és a 0,80 feletti értékek azt jelzik, hogy a modell jó munkát végez a célváltozónkat alkotó két kategória megkülönböztetésében. Összehasonlíthatjuk az 1. és 2. modell ROC és AUC értékeit, amelyek erős különbséget mutatnak a teljesítményben. Mindenképpen azt szeretnénk, ha a ROC-diagramjaink inkább az 1-es modell (balra), mint a 2-es modell (jobbra) ábrájához hasonlítanának!

library(ROCR)par(mfrow=c(1, 2))prediction(test.predicted.m1, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()prediction(test.predicted.m2, test$default) %>% performance(measure = "tpr", x.measure = "fpr") %>% plot()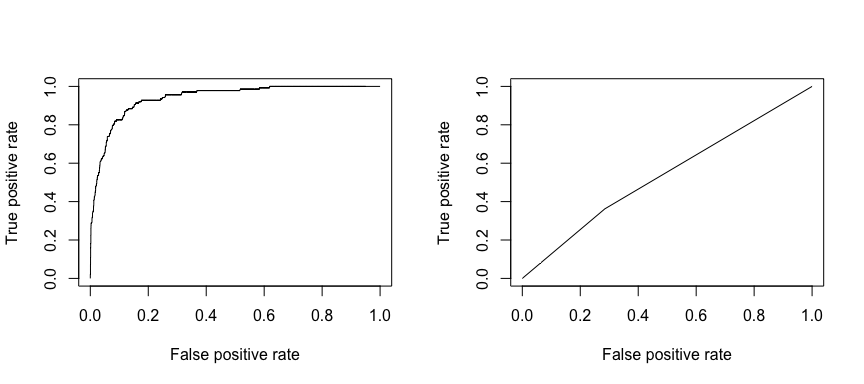

Az AUC numerikus kiszámításához pedig az alábbiakat használhatjuk. Ne feledjük, hogy az AUC 0,50 és 1,00 között mozog. Így a 2. modell egy nagyon rossz osztályozó modell, míg az 1. modell egy nagyon jó osztályozó modell.

# model 1 AUCprediction(test.predicted.m1, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.939932# model 2 AUCprediction(test.predicted.m2, test$default) %>% performance(measure = "auc") %>% [email protected]## ]## 0.5386955

A modelleket tovább “hangolhatjuk”, hogy javítsuk ezeket az osztályozási arányokat. Ha javítani tudjuk az AUC és a ROC görbéket (ami azt jelenti, hogy javítjuk az osztályozási pontossági arányokat), akkor “liftet” hozunk létre, ami azt jelenti, hogy megemeljük az osztályozási pontosságot.

Kiegészítő források

Ezzel a logisztikus regresszióval megismerkedhetünk. Ne feledje, hogy sokkal több mindenbe beleáshatja magát, így a következő források segítenek többet megtudni:

An Introduction to Statistical Learning
Applied Predictive Modeling
Elements of Statistical Learning

Ez az oktatóanyag az An Introduction to Statistical Learning 2

4. fejezet 3. szakaszának kiegészítéseként készült.