A mai bejegyzésben megismerheted a különbséget a prímszámok és az összetett számok között. Emellett számos példát is mutatunk, hogy jobban megértsd őket.
Index
Mik a prímszámok?
A prímszámok azok a számok, amelyek csak önmagukkal és 1-gyel oszthatók, vagyis ha megpróbáljuk őket egy másik számmal osztani, az eredmény nem egész szám. Ha tehát a számot nem eggyel vagy önmagával osztjuk, akkor olyan maradékot kapunk, ami nem nulla.
Prímszámok 100-ig
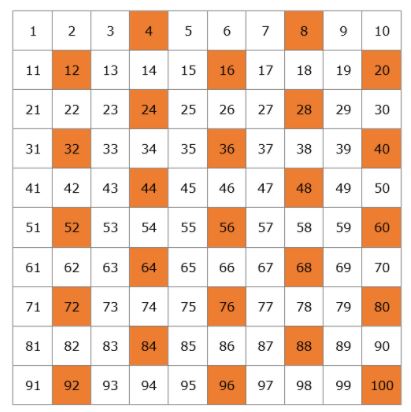
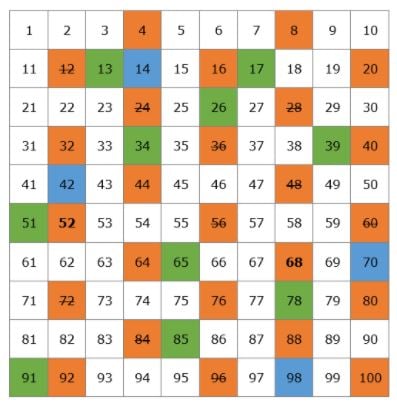
Elkészítünk egy táblázatot az összes prímszámmal, ami 100-ig létezik.
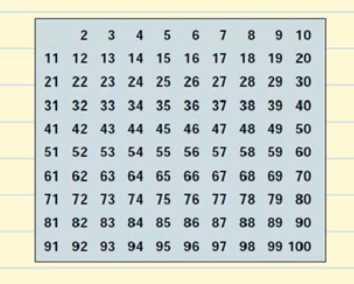
Kezdjük a 2-vel. A 2 egy prímszám, de a 2 minden többszöröse összetett szám lesz, mivel 2-vel osztható. A táblázatból kihúzzuk a 2 összes többszörösét.
A következő prímszám a 3, így a 3 összes többszörösét kihúzhatjuk, mivel azok összetett számok lesznek.
A 3 után a következő prímszám az 5, így kihúzzuk az 5 összes többszörösét.
Aztán itt van a 7-es prímszám, és kihúzzuk a 7 összes többszörösét.
A következő prímszám a 11, így kihúzzuk a 11 összes többszörösét, amelyek a 22, 33, 44, 55, 66, 77, 88 és 99-esek. Ezeket a számokat már mind áthúztuk, így befejeztük az összes összetett szám áthúzását a táblázatunkon.

Ez a prímszámok listája 1-től 100-ig. Nem kell megjegyezned őket, de a legjobb lenne, ha a kisebb számokat megjegyeznéd, mint például a 2, 3, 5, 7, 11, 13.
Hány prímszám van?
A görög matematikus Eratoszthenész (Kr. e. 3. század) kidolgozott egy gyors módszert arra, hogy megtaláljuk az összes prímszámot egy adott számig. Ezt az eljárást Eratoszthenész szitájának nevezik.
Megjegyezzük, hogy 1 és 100 között 25 prímszám van. Hány prímszám van összesen? Már az ókor óta tudjuk, hogy végtelen sok van, ezért lehetetlen mindet felsorolni. Mivel Euklidész, aki a Kr. e. 4. században elsőként mutatta ki, hogy végtelen sok van, nem ismerte a végtelen fogalmát, azt mondta, hogy “a prímszámok többen vannak, mint bármely rögzített sokaságuk”, ami azt jelenti, hogy ha 100-at képzelünk el, még több van, és ha egymilliót képzelünk el, még több van.
Prímszámok 100-tól 1000-ig
Nézzük meg a prímszámokat 100-tól 1000-ig.

Sajnáljuk, hogy nem tudjuk mindet megmutatni, hiszen tudod, hogy végtelen sok van belőlük. 😉
Prímszámok példák
Azért, hogy jobban megértsd a prímszámokat, elmagyarázunk egy feladatot.
Sarának van 6 darab cukorkája, amit meg akar osztani, de nem tudja, hány emberrel oszthatja meg úgy, hogy mindenki ugyanannyit kapjon, és egy se maradjon. Hányféleképpen tudja ezt megtenni?
Itt van Sara és a 6 darab cukorka:

Hogyan oszthatjuk meg őket?
Az első és legegyszerűbb módja, hogy egy embernek adjuk, vagyis osztjuk el 1-gyel. Így annak az embernek 6 darab cukorkája lesz.
A következő lehetőség, hogy 2 ember között osztjuk el őket. Mivel 6 osztva 2-vel 3, minden személy 3 darab cukorkát kap!

Folytassuk a következő számmal, a 3-mal. Ha 6 darab cukorkát elosztunk 3 ember között, az is egy pontos osztás, és minden személy 2 darab cukorkát kap:

Folytassuk a számokkal. A 4 és az 5 esetében nincs pontos osztásunk, de a 6 esetében igen.
Mivel 6 osztva 6-tal 1, akkor 6 gyereknek adhatunk fejenként 1 darab cukorkát.

Összegyűjtünk néhány információt. Van 6 darab cukorkánk, amit (pontos osztással) megoszthatunk 1, 2, 3 és 6 ember között. Más szóval, a 6-os számot el tudjuk osztani, és 0-t kapunk maradékként, ha elosztjuk 1, 2, 3 és 6-tal. Ezeket a számokat a 6 osztóinak nevezzük.
Kipróbáljuk egy másik számmal, például a 7-essel.
Most Sara-nak van 7 darab cukorkája, és szeretné megosztani, de nem tudja, hány emberrel tudja megosztani úgy, hogy mindenki ugyanannyit kapjon, és egy se maradjon. Hányféleképpen tudja ezt megtenni?

Henry olyan szerencsés! Megkapta az összes cukorkát!
Van más módja is? A 7-et nem oszthatjuk 2-vel, 3-mal, 4-gyel, 5-vel vagy 6-mal, …de a 7-et igen!
Sara megoszthatja a cukorkadarabokat 7 ember között, adva nekik egy-egy darabot:

A 7 tehát csak 1-gyel és 7-tel osztható, egyetlen osztója az 1 és a 7! Ezeket a számokat hívjuk prímszámoknak.
Létezik még több prímszám? Hát persze! Keressünk még néhányat:
- A 4? Nem! Mert az osztói 1, 2 és 4.
- Az 5? Igen! Mert az osztói 1 és 5.
- A 8? Nem! Mert az osztói 1, 2, 4 és 8.
Röviden, egy szám prímszám, ha csak 2 osztója van: 1 és önmaga.
Most már rengeteg prímszámot kereshetsz!
Hogyan találjunk prímszámokat
Figyelj nagyon! Adunk egy trükköt, amivel megtudhatod, hogy egy szám prímszám-e vagy sem, anélkül, hogy meg kellene keresned az osztóit, de olyan módon, ami sokkal szórakoztatóbb, és megadja nekünk az osztóit (ha vannak).
Válasszunk egy véletlenszerű számot, például a 16-ot.
Hogy ellenőrizzük, hogy prímszám-e vagy sem, egy táblázatot fogunk használni, ami nagyon hasonlít a Montessori kártyák szorzásához. És annyi golyót fogunk kapni, ahány számot választottunk. Ebben az esetben 16 golyót.
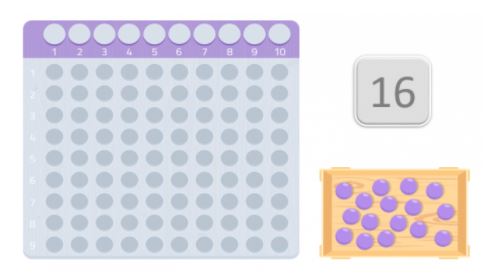
Mihelyt megvan a táblázat és a golyók, az első hellyel kezdve helyezzük el őket az asztalon, és próbáljunk meg egy téglalapot alkotni. A téglalap széleit alkotó számok az adott szám osztói.
Amennyiben csak az általunk használt számmal és az 1-es számmal sikerül téglalapot alkotnunk, akkor az egy prímszám lesz.
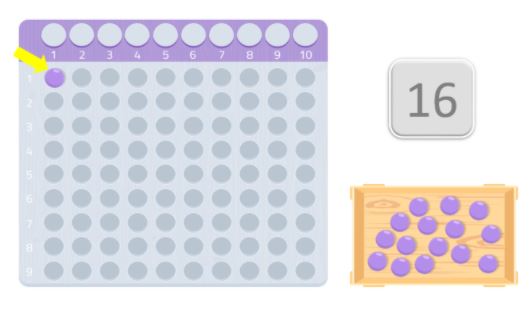
Ez esetben például az első sorba 8 golyót, a másodikba pedig további 8-at teszünk. Mint láthatjuk, egy téglalapot alakítottunk ki, és láthatjuk, hogy a 8, akárcsak a 2, a 16-os szám osztója. Ezért a 16 nem prímszám, mert mint tudjuk, prímszámok azok a számok, amelyek csak önmagukkal és 1-gyel oszthatók.
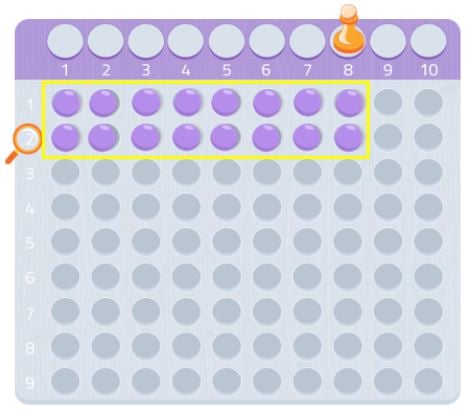
Megpróbálhatjuk egy másik számmal, például a 7-gyel.
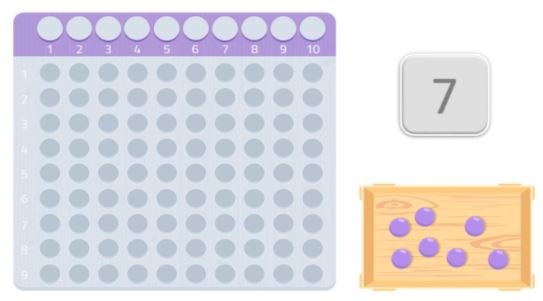
Amint látjuk, nem tudnánk teljes téglalapot alkotni, hiányozna egy gömb. Mivel nem tudunk téglalapot alkotni, azt mondhatjuk, hogy a 7-es számnak nincs más osztója önmagán és 1-en kívül, ahogy a következő képen is láthatjuk.
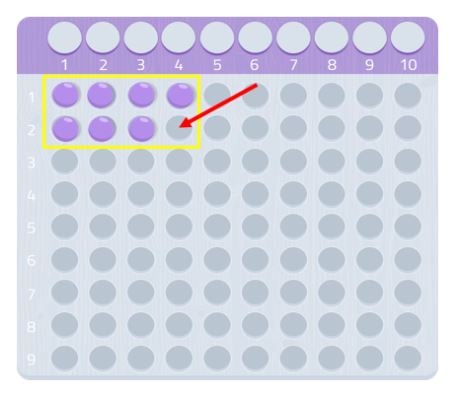
Ezért a 7 egy prímszám!
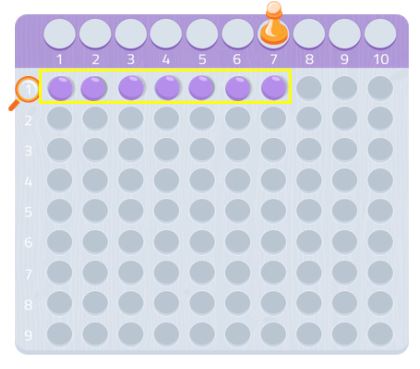
Próbáljuk ki bármely más számmal, meglátjuk, hogyan működik! Használhatsz grafikonpapírt, és kereshetsz olyan téglalapokat, amelyekben ennyi négyzet van.
Miért fontosak a prímszámok?
A prímszámok a számtan kulcsai, az alábbiakban egy példát láthatsz, amely bemutatja fontosságukat, nemcsak a matematikában, hanem a természetben is.
Mit értünk azon, hogy a prímszámok a számtan kulcsai?
Ez azért van, mert minden szám egy egyedi szorzatból áll, amely ezen számok sorozatából áll.
Az a feltételezés, hogy körülbelül 20 000 éve tanulmányozzák őket, amikor egy ősünk feljegyezte a prímszámok sorozatát (11, 13, 17 és 19) az Ishango-csontra. Mintha ez véletlen lenne, megerősítették, hogy az ókori egyiptomiak már 4000 évvel ezelőtt is foglalkoztak velük.
A természet ráadásul nagyon jól ismeri őket, és egyes fajok evolúciójuk során képesek voltak felfedezni őket, és kihasználni őket a túlélés érdekében.
A kabócák több fajára gondolok, például az Észak-Amerikában élő Magicicada septendeciumra. Ez a kabócafaj 13 vagy 17 év körül alakította ki szaporodási ciklusát, nem 12, 14, 15, 16 vagy 18 – pontosan 13 vagy 17 év körül. Ez lehetővé teszi számukra, hogy elkerüljék a ragadozókat, amelyeknek szintén periodikus szaporodási ciklusuk van; képzeljünk el egy ragadozót, amelynek 4 éves szaporodási ciklusa van.
Ha egy kabóca életciklusa 12 vagy 14 év lenne, akkor nagyon gyakran esne egybe egy ragadozóval, sokkal gyakrabban, mintha 13 vagy 17 év lenne. Pontosan 100 évente 2 alkalommal, míg egyébként 11 ciklusban esnének egybe, ami veszélyeztetné a faj fejlődését.”
Az elektronikus kommunikáció biztonsága is a prímszámokon alapul. Minden interneten keresztül küldött titkosított üzenethez (üzenethálózatok, vásárlások vagy elektronikus banki ügyintézés) egy-egy nagyszám tartozik, és nagyon nehéz megállapítani, hogy hol prímszám, hol nem. A címzettnek megvan az egyik osztója, és ezért tudja visszafejteni. Tehát a prímszámok megléte kritikus a magánéletünk szempontjából, amikor elektronikusan kommunikálunk.
Mik az összetett számok?
Az összetett számok azok a számok, amelyek oszthatók 1-gyel és önmagukkal, valamint más számokkal.
Megnézünk egy példát egy prímszámra és egy összetett számra.
A 11 felírható az 1 x 11 szorzataként, de nem írható fel a természetes számok bármely más szorzataként. Csak az 1 és a 11 osztója van, ezért prímszám.
12 felírható az 1 x 12 szorzataként, valamint a 3 x 4 és a 2 x 6 szorzataként. Mivel a 12 több számmal osztható, mint 1 és önmaga, a 12 összetett szám.
Az 1 prímszám?
Vannak emberek, akik ezt hiszik, mert azt mondják, hogy az 1 csak 1-gyel és önmagával osztható, de a matematikában az 1-et mint prímszámot elvetették, mert csak egy osztója van. Valójában az “egy pozitív egész szám akkor prímszám, ha pontosan két pozitív osztója van” kritériumot használják arra, hogy az egyes számot kizárják a prímszámok közül. Nem azért, mert válogatósak vagyunk, de ha az egyes számot prímszámnak tekintenénk, akkor sok matematikai tulajdonságot másképp kellene kimondani.
Az 1 tehát összetett szám?
Nos, ez sem összetett szám, hiszen nem lehet prímszámok szorzataként feltenni. Az 1-es szám nem prímszám és nem összetett szám. És mielőtt megkérdeznéd, a nulla sem prím vagy összetett szám, de ez azért van, mert minden olyan megfontolás, amit a pozitív számokra, vagyis a nullánál nagyobb számokra magyaráztunk.
Egy szám osztói
Egy szám osztója az az érték, amely a számot pontos részekre osztja, vagyis amelynek maradványa 0 maradványa van.
Példaként a 24 osztóit fogjuk kiszámítani.
Az osztást a legkisebb számokkal kezdjük, kezdve az 1-gyel.
- 24 / 1 = 24. Mind az 1, mind a 24 osztószám.
- 24 / 2 = 12. Tehát 2 és 12 osztók.
- 24 / 3 = 8. Tehát 3 és 8 osztók.
- 24 / 4 = 6. Tehát 4 és 6 osztók.
- 24 / 5 = 4. Tehát 4 és 6 osztó. Ez nem egzakt osztás, és a maradék 4, tehát 5 nem osztó.
A következő szám a 6, de mivel már tudjuk, hogy 6 24 osztója, befejeztük a 24 osztóinak kiszámítását.
Videó: Faktorizáció és prímszámok
Ha többet szeretnél megtudni a prím- és összetett számokról, nézd meg a következő videót. A faktorálás fogalmát is megismerheted a Montessori-táblázat segítségével.
Ez a videó az interaktív oktatóanyagaink közé tartozik, és bár nem interaktív, mégis annyiszor megnézheted, ahányszor csak akarod, és megoszthatod barátaiddal. Ha szeretne hozzáférni interaktív oktatóanyagainkhoz, regisztráljon a Smartick oldalon! Az online módszer, amely segít a 4 és 14 év közötti gyerekeknek a matematika tanulásában és gyakorlásában.
Ha szeretnél tovább tanulni a prímszámokról és a legjobb, a szintedhez igazodó matematikáról, regisztrálj a Smartickre és próbáld ki ingyen!
Tudj meg többet:
- Prímszámok és összetett számok
- Prímszámok: A Trick to Help You Identify Them
- Prime Numbers:
- Learn How to Find them with the Sieve of Eratosthenes
- Learn How to Factor into Prime Numbers
- Prime Numbers Activities with Smartick



- Autor
- Újabb bejegyzések
Matematikusokból, tanárokból, professzorokból és más oktatási szakemberekből álló multidiszciplináris és multikulturális csapat!
A lehető legjobb matematikai tartalmak létrehozására törekszenek.
- Példák 3. osztályos matematikai szöveges feladatokra megoldásokkal – 03/25/2021
- Folytonos belső szögek: Mik ezek és hogyan találjuk meg őket példákkal – 03/11/2021
- Példák második osztályos szófeladatokra megoldásokkal – 02/04/2021